本文将介绍一种最简单的自适应过滤移动平均计算的预测方法，并给出相应的代码实现。代码我原本是用 MatLab 写的，因为后来觉得比较好用，所以决定用 Python 重新写一遍。但是重写之后在 Python 里执行的效果跟 Matlab 很不一样。 具体的原因和情形在下面讨论；

算是学习笔记，这是一段最简单的自适应过滤方法。代码是我自己编写的，但是算法是老师上课教的，是对一段给定的序列数据进行自适应过滤的计算。

我们今天的目标比较简单，就是 预测全国香蕉年度产量数据。数据来源是 National Data 国家统计局数据网站

id	年份	香蕉	id	年份	香蕉
26	2003	590.33	36	2013	1103
27	2004	605.61	37	2014	1062.15
28	2005	651.81	38	2015	1062.7
29	2006	690.12	39	2016	1094.03
30	2007	763.95	40	2017	1116.98
31	2008	748.43	41	2018	1122.17
32	2009	829.65	42	2019	1165.57
33	2010	884.1	43	2020	1151.33
34	2011	946.07	44	2021	1172.42
35	2012	1035.98	45	2022	1177.68

原理的介绍

原理的简单介绍如下：

1. 基本公式的介绍

总的来说，自适应过滤移动平均法是对时间序列观测值进行加权平均来预测未来值。

基本预测公式：

$${\hat{X}}_{t+1}={\omega }_0{X}_t+{\omega }_1{X}_t-1+\cdots {\omega }_N{X}_{t-N+1}+e_t$$

其中：

• ${\hat{X}}_{t+1}$ 为第 t+1 期的预测值
• $X_{t-i+1}$ 为第 t-i+1 期的观测值
• ${\omega }_1$ 为第 t-i+1 期观测值的权数
• $N$ 为权数的个数

初始权重的计算公式非常简单：

$${\omega }_i=\frac{1}{N}$$

然后是重新计算权重的公式：

$${\omega }_i^{{}^{\prime }}={\omega }_i+2\times k\times e_t\times X_{t-i-1}$$

其中，$k$ 的计算方法是：

$$k\le \frac{1}{\left[\sum _{i=1}^N{X}_i^2\right]max}$$

而残差 $e_t$ 的计算方法是：

$$e_t=X_t-{\hat{X}}_t$$

我这里解释一下这个公式：

简单的来说，就是对于给出的时间序列数据，用前 N 期的数据计算第 N+1 期的预测值。再根据新产生的预测值和原始值的差值，计算新的权重。然后拿新的权重计算下面一期的值，如此重复循环很多次，得到理想的预测结果。

比如，我们现在有 10 组数据，选定 $N=3$。这样就产生了一组权重 ${\omega }_0$、${\omega }_1$、${\omega }_2$

$N$ 个初始权重都是相等的。如果我们这里是 $N=3$，那么这里有：

$${\omega }_0={\omega }_1={\omega }_2=\frac{1}{3}=0.3333$$

（保留四位小数）

然后我们首先用 1、2、3 期数据计算第 4 期的值，求残差，根据第 4 期的预测值和第四期真实值之间的残差计算新的权重

然后用 2、3、4 期数据计算第 5 期的值，求残差，根据第 5 期的预测值和第四期真实值之间的残差计算新的权重

再用第 4、5、6 期数据计算第 7 期的值，求残差，根据第 6 期的预测值和第四期真实值之间的残差计算新的权重

……

以此类推，直到 10 组数据全部用完。每一次重新计算权重的时候，这个时候我们就会得到 6 个预测值。这样就能计算出一个总残差 $\sum et$，是各期预测值的和。还能得到 3 个经过迭代后的权重：

重复我们上述的操作。把我们刚才计算出来的三个新的权数，也就是 10 次重复迭代时的 ${\omega }_0$、${\omega }_1$、${\omega }_2$，重新作为新的权数，重复上述的 10 次迭代。

反复重复之后，就能获得最优的一组权 ${\omega }_i$。用这组权数就能预测将来的数据的走势。

以迭代 N 次之后的总残差的值不再变化为权值达到最优的判别标准。 但是如何判断 总的残差不再变化 本身就挺困难的。甚至在实践中还发现 Python 和 MatLab 中取得最好效果时的计算方法不一样。

2. 权数 N 的选择

为了减少工作量和提高预测精度，预测模型的权数的个数尽量取得恰当。

1. 序列中不存在季节模型时，N = 2 或 3

2. 存在季节模型取 N = L

3. 调整常数 k 的选择

关于如何选择 k，课本上是这么说的：－序列中最大的N个值的平方和的倒数

但是在代码实践的过程中，我遇到了这样的几个问题：

1. 根据上述方法计算出来的 k 的值明显太大，不符合要求。这导致算法迭代的过程中总残差不断向无穷大逼近、权数的逼近失去控制。

2. Python 和 MatLab 在迭代时取得最好效果（总残差最小时）的 k 值不相同。在 MatLab 中，取得 k = 0.00000001 时效果理想，而在 Python 中，取得 k = 0.0000000007 时效果最好。

造成问题的原因我现在尚不清楚。可能随着以后学习的深入会了解的。

Python 的实现方法

引入需要用到的库

numpy 和 matplotlib 老熟人，我大概不需要介绍了。

import numpy as np
import matplotlib.pyplot as plt

如果没有安装过，则在终端里运行下面的命令安装：

pip3 install numpy
pip3 install matplotlib

用于迭代的函数

根据上面的迭代规则，可以写出下面的函数：

def self_adaptive( seq, N, k, maxsteps ):
    ## 初始化序列
    seq_ada = np.zeros( len(seq) )  # 设置预测序列的初始数字是 0
    et = np.zeros( len(seq) )       # 设置误差序列的初始数字是 0
    sum_abs_et = sum(seq)

    ## 计算初始权值
    w = np.ones( (N, 1) )
    w = w/N

    ## 计算 "残差不再变化" 的判别标准
    min_Err = 1 / ( np.max(seq) )

    ## 把 maxsteps 交给 step 用于迭代计算
    # maxsteps 并不参与计算
    step = maxsteps

    ## 主事件循环
    while (step >= 0):
        for i in range( N, ( len(seq) ) ):
            seq_ada[i] = (seq[ (i-N):(i) ]@np.flipud(w))[0] 
            et[i] = seq[i] - seq_ada[i]

            # 重新计算权重
            # 这里原本是不想用循环的，希望通过 NumPy 的矩阵运算搞定
            # 但是反复调整了很多次，语法一直在报错
            # 索性不改了
            for j in range(0, N):
                w[j] = w[j] + 2*k*et[i]*seq[i-j]

        ## 输出每一步的权重和残差
        # 我这里暂时注释掉了。
        # print(f"at step : {step: 20d}")
        # print(w)
        # print(sum(abs(et)))

        # 循环的停止条件是误差的大小不再发生变化
        # 也就是上一循环得出的总误差和这一轮循环的总误差的差值很小
        # 这里取 min_Err 作为比较的值
        if( abs(sum_abs_et - sum( abs(et))) < min_Err ):
            print(f"solving stoped : at step {maxsteps-step:10d}")
            print(step)
            break
        else:
            sum_abs_et = sum(abs(et))
        step = step - 1;

    return [seq_ada, w, et, sum_abs_et ]

注意几个问题

1. np.ones() 和 np.zeros() 的使用

如果想要构建 3 * 4 的 [0] 矩阵，应当写作 np.zeros( (3, 4) )，可以看见嵌套了两层括号。这是因为 np.zeros() 和 np.zeros() 只传入一个参数。

2. 循环的停止

这里给循环停止设置了两个条件：
- 设定的步数全部用完，自然退出循环
- 设定的步数没有用完，但是残差不再发生变化，退出循环

那么就会产生下面的这几种情况：

1. 循环自然结束
2. 循环在中途停止了

对于第二种情况，当然是比较理想的。由于总的残差不再变化，那么结果就已经逼近最优的预测结果。

但对于第一种情况，则需要讨论了。

造成第一种情况的原因基本有两张，可能是因为：

1. 过迭代，导致错过了残差最小的时机。从而 ${\omega }_i$ 继续迭代，但是越发偏离最优的情形。

2. 循环的最大步数设置不够，以至于还没有达到最小残差和最优权重的组合，就结束了循环。

对于 1，我们应当修改学习率，而且一般是减小学习率。对于 2，则应该增加最大步数。

参考下面的流程图：

问题我们应该如何判断属于那一种情况呢？

我这里想到的解决办法：让代码输出每一步迭代步骤，然后盯着屏幕观察。

显然，这种解决方案是很牵强的，但是有效。

我这里暂时把输出每一步的代码给注释掉了。否则的话，我的 Jupyter Notebook 展示结果将会非常的…… 长

3. 计算 “残差不再变化” 的判别标准

正如上文所言，如何判断 总的残差不再变化 本身就挺困难的。甚至在实践中还发现 Python 和 MatLab 中取得最好效果时的计算方法不一样。

具体来说，在 MatLab 中，以学习率 k 作为判别标准就能取得很好的效果。当总残差减去新的计算产生的残差小于 k 的时候就认定是已经达到了最优的结果。

而在 Python 中，我却发现使用 min_Err = 1 / ( np.max(seq) ) 的效果最理想。

下面的函数用于绘图，展示预测曲线和原始观测值曲线的图，便于直观地查看预测的符合程度：

## 函数，用于计算结果的可视化
def plot_result(N, seq, seq_ada, additional_xrange = 0):
    # additional_xrange 是为了方便后面
    # 既可以画带有后 n 期预测值的图像
    # 也可以画预测数据和原始数据的对比图
    # 这样能让函数更加灵活

    # 自动调整绘图区域大小
    plt.xlim( N, len(seq)+additional_xrange )
    plt.ylim( min(seq)-max(seq)/len(seq), max(seq)+max(seq)/len(seq) )

    # 绘图
    plt.plot(seq, label = "original")
    plt.plot(seq_ada, label = "fit")

    # 添加图例
    plt.legend(loc="lower right")

然后下面是写进主函数的内容：

要注意这里的数据类型是 array 类型。在初始化 array() 类型的时候要传入一个空列表 []，否则会由于缺少必要参数而报错。

## 数据的设置

# 全国香蕉产量
BANANA = np.array([  590.33,  605.61,  651.81,  690.12,  763.95, 
                     748.43,  829.65,   884.1,  946.07, 1035.98, 
                       1103, 1062.15,  1062.7, 1094.03, 1116.98, 
                    1122.17, 1165.57, 1151.33, 1172.42, 1177.68 ])

## 参数的设置

N = 4                                                        # 权数
k = 0.0000000007                                             # 学习率
steps = 20000000                                             # 最大迭代次数

## 初始化变量
BANANA_ada = np.array([])
w = np.array([])
et = np.array([])
sum_abs_et = 0

调用我们刚才写好的迭代函数，在 Jupyter Notebook 里统计代码执行的时间：

%%time
## 调用函数进行自适应计算
[ BANANA_ada, w, et, sum_abs_et ] = self_adaptive(BANANA, N, k, steps)

终端输出如下：

solving stoped : at step      37640
19962360
CPU times: total: 7.73 s
Wall time: 7.75 s

可以看见代码在第 37640 次循环停了下来。

随即，我们输出结果如下：

## 输出预测结果

print("自适应过滤法的预测值为：")
print(BANANA_ada)
print("权向量：")
print(w)
print("残差：")
print(et)
print("总残差：")
print(sum_abs_et)

以下是命令行输出的结果：

自适应过滤法的预测值为：
[   0.            0.            0.            0.          723.73959593
  814.2289668   779.06532716  865.79798858  930.44496509 1006.23322428
 1103.00084065 1174.95540464 1090.82023881 1055.01113672 1090.03887229
 1132.81826258 1135.03980383 1182.91818712 1159.46463323 1177.91724331]
权向量：
[[ 1.36211585]
 [ 0.05894816]
 [-0.19148692]
 [-0.23502124]]
残差：
[ 0.00000000e+00  0.00000000e+00  0.00000000e+00  0.00000000e+00
  4.02104041e+01 -6.57989668e+01  5.05846728e+01  1.83020114e+01
  1.56250349e+01  2.97467757e+01 -8.40653916e-04 -1.12805405e+02
 -2.81202388e+01  3.90188633e+01  2.69411277e+01 -1.06482626e+01
  3.05301962e+01 -3.15881871e+01  1.29553668e+01 -2.37243305e-01]
总残差：
513.1131300794887

根据上述计算的输出结果，我们可以知道：建立的模型为：

权向量：

$${\hat{X}}_{t+1}=1.3621X_t+0.0589X_{t-1}-0.1915X_{t-2}-0.2350X_{t-3}$$

参考下面的表格：

id	year	banana	banana_ada
26	2003	590.33	x
27	2004	605.61	x
28	2005	651.81	x
29	2006	690.12	x
30	2007	763.95	723.7395959
31	2008	748.43	814.2289668
32	2009	829.65	779.0653272
33	2010	884.1	865.7979886
34	2011	946.07	930.4449651
35	2012	1035.98	1006.233224
36	2013	1103	1103.000841
37	2014	1062.15	1174.955405
38	2015	1062.7	1090.820239
39	2016	1094.03	1055.011137
40	2017	1116.98	1090.038872
41	2018	1122.17	1132.818263
42	2019	1165.57	1135.039804
43	2020	1151.33	1182.918187
44	2021	1172.42	1159.464633
45	2022	1177.68	1177.917243

通过可视化，可以看见预测的效果。

## 绘图
plot_result(N, BANANA, BANANA_ada)

利用取得的结果进行预测

模型的预测很简单，就像之前执行的步骤一样。

只不过后面的数据要使用预测产生的序列，而不是原始的观察数据。因为原始数据只有 20 个，超过了 20 个就没数了。

参考下面这张表：在预测 2024 年的香蕉产量的时候，被加粗的这几个表格里的元素将会被乘以权数来计算新的 2024 年的预测值。

id	year	banana	banana_ada
…	…	…	…
41	2018	1122.17	1132.818263
42	2019	1165.57	1135.039804
43	2020	1151.33	1182.918187
44	2021	1172.42	1159.464633
45	2022	1177.68	1177.917243
46	2023	x	1178.784821
47	2024	x	o

还不懂的话我就直说，也就是：

$${\hat{X}}_{2024}=1.3621\times 1178.78+0.0589\times -0.1915\times 1177.68-0.2350\times 1178.78$$

让我们来写一个用于预测的函数：

def calc_ada( seq, w, num ):
    # seq 是原始值序列，w 是权重向量，num 是预测期数 
    seq_pre = seq
    N = len(w)
    for i in range(num):
        seq_pre = np.append( seq_pre, ( seq_pre[ (len(seq) + i - N):(len(seq) + i ) ]@np.flipud(w) )[0] )
    return seq_pre

然后获得最后的预测结果：

## 往后预测的期数
num = 5

# 计算往后 num 期的预测值
BANANA_pre = calc_ada(BANANA, w, num)

# 打印预测结果
print("预测结果：")
print(BANANA_pre)

# 预测结果绘图
plot_result(N, BANANA, np.append(BANANA_ada[0:], BANANA_pre[len(BANANA):len(BANANA_pre)]), num )

终端输出：

预测结果：
[ 590.33        605.61        651.81        690.12        763.95
  748.43        829.65        884.1         946.07       1035.98
 1103.         1062.15       1062.7        1094.03       1116.98
 1122.17       1165.57       1151.33       1172.42       1177.68
 1178.85025437 1180.06258696 1175.81908956 1168.65011913 1158.12782402]

完整代码

这里的完整代码我做了一些简单的修改。

"""  Python 简单的自适应过滤移动平均预测方法  """

"""
    使用方法：
    1. 主函数里的 BANANA 就是预测的香蕉产量。
       如果想要预测其他数据，直接修改成其他的值就好。
    2. 图像会保存到代码同级目录下面。
       - `fit.png` 是预测曲线和原始曲线的对比图
       - `predict.png` 还包含往后预测 n 期的数据
       可以根据需要自行修改目录。
"""

" 需要用到的库 "
import numpy as np
import matplotlib.pyplot as plt

" 用于迭代的函数 "
def self_adaptive( seq, N, k, maxsteps ):
    ## 初始化序列
    seq_ada = np.zeros( len(seq) )  # 设置预测序列的初始数字是 0
    et = np.zeros( len(seq) )       # 设置误差序列的初始数字是 0
    sum_abs_et = sum(seq)

    ## 计算初始权值
    w = np.ones( (N, 1) )
    w = w/N

    ## 计算 "残差不再变化" 的判别标准
    min_Err = 1 / ( np.max(seq) )

    ## 把 maxsteps 交给 step 用于迭代计算
    # maxsteps 并不参与计算
    step = maxsteps

    ## 主事件循环
    while (step >= 0):
        for i in range( N, ( len(seq) ) ):
            seq_ada[i] = (seq[ (i-N):(i) ]@np.flipud(w))[0] 
            et[i] = seq[i] - seq_ada[i]

            # 重新计算权重
            # 这里原本是不想用循环的，希望通过 NumPy 的矩阵运算搞定
            # 但是反复调整了很多次，语法一直在报错
            # 索性不改了
            for j in range(0, N):
                w[j] = w[j] + 2*k*et[i]*seq[i-j]

        ## 输出每一步的权重和残差
        # 我这里暂时注释掉了。
        # print(f"at step : {step: 20d}")
        # print(w)
        # print(sum(abs(et)))

        # 循环的停止条件是误差的大小不再发生变化
        # 也就是上一循环得出的总误差和这一轮循环的总误差的差值很小
        # 这里取 min_Err 作为比较的值
        if( abs(sum_abs_et - sum( abs(et))) < min_Err ):
            print(f"solving stoped : at step {maxsteps-step:10d}")
            print(step)
            break
        else:
            sum_abs_et = sum(abs(et))
        step = step - 1;

    return [seq_ada, w, et, sum_abs_et ]

" 用于计算结果的可视化的函数 "
def plot_result(N, seq, seq_ada, save_as="./Figure.png", additional_xrange = 0):
    # additional_xrange 是为了方便后面
    # 既可以画带有后 n 期预测值的图像
    # 也可以画预测数据和原始数据的对比图
    # 这样能让函数更加灵活

    # 自动调整绘图区域大小
    plt.xlim( N, len(seq)+additional_xrange )
    plt.ylim( min(seq)-max(seq)/len(seq), max(seq)+max(seq)/len(seq) )

    # 绘图
    # 注意这里 line1 和 line2 后面要加上一个逗号
    # 这是因为 plot 返回 的 list 对象（list of Line2D）需要解构
    line1, = plt.plot(seq, label = "original")
    line2, = plt.plot(seq_ada, label = "fit")

    # 添加图例
    plt.legend(loc="lower right",
               handles=[line1, line2],
               labels=['original','fit'])

    # 保存图片到当前路径
    plt.savefig(save_as, dpi=1080)

" 用于预测的函数 "
def calc_ada( seq, w, num ):
    # seq 是原始值序列，w 是权重向量，num 是预测期数 
    seq_pre = seq
    N = len(w)
    for i in range(num):
        seq_pre = np.append( seq_pre, ( seq_pre[ (len(seq) + i - N):(len(seq) + i ) ]@np.flipud(w) )[0] )
    return seq_pre

" 主函数 "
if __name__=='__main__':

    print("计算时间可能较长，请耐心等候。")

    ## 数据的设置

    # 全国香蕉产量
    BANANA = np.array([  590.33,  605.61,  651.81,  690.12,  763.95, 
                         748.43,  829.65,   884.1,  946.07, 1035.98, 
                           1103, 1062.15,  1062.7, 1094.03, 1116.98, 
                        1122.17, 1165.57, 1151.33, 1172.42, 1177.68 ])

    ## 参数的设置

    N = 4             # 权数
    k = 0.0000000007  # 学习率
    steps = 20000000  # 最大迭代次数

    ## 初始化变量
    BANANA_ada = np.array([])
    w = np.array([])
    et = np.array([])
    sum_abs_et = 0

    ## 调用函数进行自适应计算
    [ BANANA_ada, w, et, sum_abs_et ] = self_adaptive(BANANA, N, k, steps)

    ## 输出预测结果

    print("自适应过滤法的预测值为：")
    print(BANANA_ada)
    print("权向量：")
    print(w)
    print("残差：")
    print(et)
    print("总残差：")
    print(sum_abs_et)

    ## 绘图
    plot_result(N,
                BANANA,
                BANANA_ada,
                "./fit.png")

    ## 往后预测的期数
    num = 5

    # 计算往后 num 期的预测值
    BANANA_pre = calc_ada(BANANA, w, num)

    # 打印预测结果
    print("预测结果：")
    print(BANANA_pre)

    # 预测结果绘图
    # 预测结果绘图
    plot_result(N, BANANA,
            np.append(BANANA_ada[0:],
            BANANA_pre[len(BANANA):len(BANANA_pre)]),
            "./predict.png",
            num )

MatLab 的实现方法

MatLab 的实现方法与 Python 的思想基本一致。很多细节上面面已经解释过了，这里就不再赘述。对于代码的用法和说明，我在代码的注释里面已经写得非常详细了。

如果不熟悉 MatLab 函数，我这里再声明一下： MatLab 函数要保存在单独的 .m 文件里面，而且文件的命名要与函数名一致。

直接给出代码：

用于迭代计算的函数 adaptive.m

function [seq_ada, w, et, sum_abs_et ] = adaptive(seq, N, k, maxsteps)
%ADAPTIVE 进行自适应预测方法的迭代
%   对于一组时序数据，对于给出的权数、学习率和最大迭代次数进行迭代
%   [seq_ada, w, et, sum_abs_et ] = adaptive(seq, N, k, maxsteps)
% 
% 输入：
% seq        : 一维行向量，是时间序列数据
% N          : 权数， w 的个数
% k          : 学习率，通常根据 k = 1 / sum[1~N](xi^2) 计算
% maxsteps   : 最大迭代次数，"如果一直等不到迭代结束"的应对办法
% 
% 输出：
% seq_ada    : 自适应预测数据，为一维行向量，开头几个数字是 0
% w          : 模型的权，为一维列向量
% et         : 序列误差
% sum_abs_et : 误差的绝对值的和
%
% 例子：[seq_ada, w ] = adaptive([2,4,6,8,10],2,0.05,18000)
% 注意事项：选择合适的 N 和 k 对于获得好的预测结果很重要。
% 文档日期：2023/06/22
% 标签：预测理论
% 创建日期：2023/06/22
% 最后更新日期：2023/06/29

%% 初始化序列
seq_ada = zeros(1, length(seq)); % 设置预测序列的前 N 个数字是 0
et = zeros(1, N);                % 设置误差序列的前 N 个数字是 0
sum_abs_et = 0;

%% 计算初始权值
w = ones(N, 1);
w = w/N;

%% 把 maxsteps 交给 step 用于迭代计算
% maxsteps 并不参与计算
step = maxsteps;
while (step >= 0)
    for i = (N+1):(length(seq))
    	seq_ada(i) =  seq( (i-N):(i-1) )*flip(w);
        et(i) = seq(i) - seq_ada(i);
        % 重新计算权重
        for j = 1:N
            w(j) = w(j) + 2*k*et(i)*seq(i-j);
        end
        disp(w)
    end
    % 循环的停止条件是误差的大小不再发生变化
    % 也就是上一循环得出的总误差和这一轮循环的总误差的差值很小
    % 这里取 k 作为比较的值
    if( abs( sum_abs_et - sum( abs(et)) ) < k )
        fprintf("solving stoped : at step %d\n", maxsteps-step) 
        break
    else
        sum_abs_et = sum(abs(et));
    end
    step = step - 1;
end

然后是用于绘图的函数 autoplot.m

function [] = autoplot(seq, seq_ada, N, save_as, adational_xrange)
%AUTOPLOT 绘制自适应移动平均方法的预测效果图像
%   自动调整和适配画幅的长款比例尺寸
%   [] = autoplot(seq, seq_ada, N, adational_xrange)
% 
% 输入：
% seq              : 一维行向量，一般是原始的时间序列数据
% N                : 权数， w 的个数
% adational_xrange : 额外的 x 的范围，通常用于 "预测未来 N 期" 的情况
% save_as          : 图片保存的路径
% 
% 输出：无
% 会绘制一张描述数据序列变化的折线图
% 默认保存为当前目录下的 ./fig.png
% 有其他图片保存需求的可以添加 
%
% 例子：autoplot([590, 606, 652, 690, 764], ...
%                [0, 0, 0, 0, 711, 792], 4)
% 注意事项：adational_xrange 和 save_as 可有可无
% 文档日期：2023/06/22
% 标签：预测理论
% 创建日期：2023/06/22
% 最后更新日期：2023/06/29

%% 按照具体使用函数时候的参数输入个数来判断
% 如果没有输入 adational_xrange，则默认为 0
if nargin == 3
    save_as = "./fig.png";
elseif nargin == 4
    adational_xrange = 0;
end

%% 绘图

% 绘图设置
grid on;
hold on;

% 绘图范围
xlim([N, (length(seq)+adational_xrange)])
ylim([(min(seq)-(max(seq)-length(seq))), ...
      (max(seq)+(max(seq)-length(seq)))])

% 绘图
plot( seq )
plot( seq_ada )
saveas(gcf, save_as)
end

然后是用于预测的函数 predict.m

function [seq_pre] = predict(seq, w, num)
%PREDICT 用于自适应过滤法的预测计算
%   对于已知的权重，计算未来 num 期的预测值
%   [seq_pre] = predict(seq, w, num)
% 
% 输入：
% seq : 原始值序列
% w   : 权重向量，为列向量
% num : 要预测的期数 
% 
% 输出：
% seq_pre : 前数期是原始时间序列，最后 num 期是预测的数据点
%
% 例子：[seq_pre] = predict(seq, w, num)
% 注意事项：seq_pre 前数期是原始时间序列，最后 num 期是预测的数据点
% 文档日期：2023/06/22
% 标签：预测理论
% 创建日期：2023/06/22
% 最后更新日期：2023/06/29

    seq_pre = seq;
    N = length(w);
    for i = 1:(num)
        disp(i)
        disp(N)
        disp(seq_pre)
        disp((length(seq)) )
        disp((length(seq)+i-N))
        disp((length(seq)+i-1))
        disp(seq_pre( ((length(seq)+i-N):(length(seq)+i-1))))
        disp(w)
        disp(flip(w))
        seq_pre = [seq_pre, ( seq_pre( ( (length(seq)+i-N):(length(seq)+i-1) ) )*flip(w) )];
    end
end

最后是主函数 main.m，注意图片的保存路径是在代码主目录下的 ./image/ 文件夹下面。如果需要设置其他路径的话，可以自行修改。

%% MatLab 自适应预测 %%

%{
    用自适应预测方法预测两周的波罗的海 BANANA 指数
%}

%% 清理工作区
clc; clear; close all;

%% 迭代数据赋值

% 2013 - 2023 全国香蕉产量数据
BANANA = [  590.33,  605.61,  651.81,  690.12,  763.95, ...
            748.43,  829.65,   884.1,  946.07, 1035.98, ...
              1103, 1062.15,  1062.7, 1094.03, 1116.98, ...
           1122.17, 1165.57, 1151.33, 1172.42, 1177.68 ];
N = 4;                                                       % 权数
k = 0.00000001;                                              % 学习率
steps = 2000000;                                             % 最大迭代次数
num = 5;

%% 调用函数进行自适应计算

[BANANA_ada, w, et, sum_abs_et ] = adaptive(BANANA, N, k, steps);


%% 输出结果

fprintf("自适应计算结果：\n\n")
fprintf("\n自适应预测的序列：\n")
disp(BANANA_ada)
fprintf("\n权向量：\n")
disp(w)
fprintf("\n误差序列：\n")
disp(et)
fprintf("\n总误差：%f\n", sum_abs_et)
fprintf("\n迭代次数：%d\n", steps)

autoplot(BANANA, BANANA_ada, N, "./image/fit.png")

%% 预测未来的值

% 这段代码是可以用的
% 我这里只是因为只想画预测序列，所以暂时注释掉了
% BANANA_pre = predict(BANANA, w, num);
% autoplot(BANANA, [BANANA_ada(1:length(BANANA)), ...
%               BANANA_pre(length(BANANA)+1:length(BANANA_pre))], ...
%               N, ...
%               "./image/predict.png", ...
%               num)
plot(BANANA_pre)
saveas(gcf, "./image/predict.png")

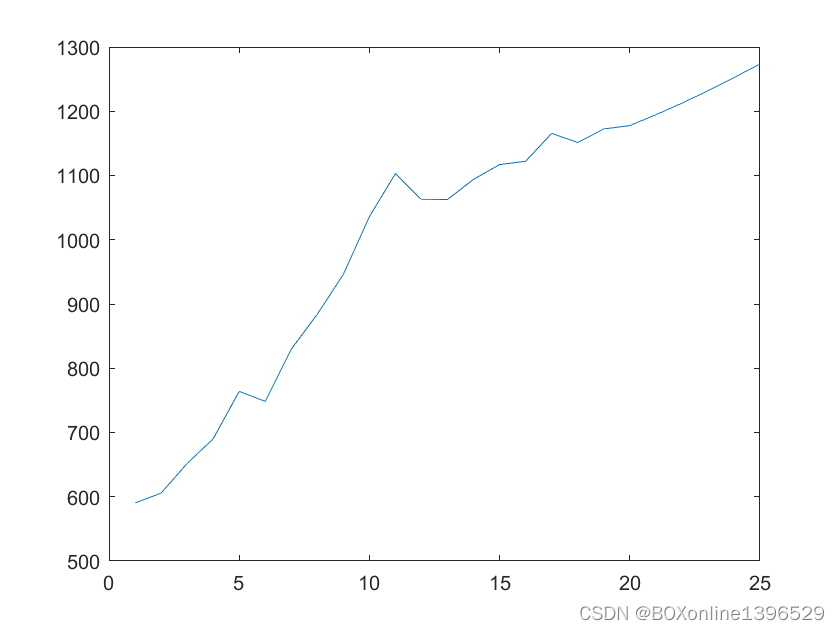
MatLab 绘图效果

预测模型与原始数据的对比如下：

预测的序列如下：