目录

一、理论基础

2.1 遗传算法

2.2 非支配排序技术

2.3 NSGAII算法

2.4 优点

2.5 缺点

2.6 实现过程

二、核心程序

三、仿真结论

---

一、理论基础

      近年来，随着多目标优化问题在工程和科学领域中的广泛应用，基于NSGAII的三目标优化算法逐渐成为了优化算法研究的热点。本文将从数学公式和原理、优缺点、实现过程等方面详细介绍基于NSGAII的三目标优化算法，并阐述其在实际应用中的优势和局限性。
       基于NSGAII的三目标优化算法是一种多目标优化算法，其主要思想是通过遗传算法和非支配排序技术来寻找多目标优化问题的最优解。

2.1 遗传算法

       遗传算法是一种基于自然进化原理的算法，其主要思想是通过模拟自然遗传过程来搜索最优解。遗传算法包括选择、交叉、变异三个基本操作。

       选择操作：选择操作是指从当前种群中选择一部分个体作为下一代种群的父代。选择操作的目的是根据适应度函数选择出适应度较高的个体。

       交叉操作：交叉操作是指将两个父代个体的染色体进行随机交换，生成两个新的子代个体。交叉操作的目的是产生新的个体，并增加种群的多样性。

        变异操作：变异操作是指随机地改变某个个体的染色体，生成一个新的个体。变异操作的目的是增加种群的多样性，避免种群陷入局部最优解。

2.2 非支配排序技术

        非支配排序技术是指将多目标优化问题中的解集分为若干个不同的等级，每个等级内的解集互相比较没有优劣之分，而不同等级之间的解集则具有支配关系。在非支配排序技术中，常用的指标是支配关系和拥挤度距离。

       支配关系：对于多个目标函数，若一个解集比另一个解集在某一个目标函数上更优，且在其他目标函数上至少有一个优于另一个解集，则称前者支配后者。

      拥挤度距离：拥挤度距离是指每个解集与其相邻解集之间的距离之和。拥挤度距离越大，说明解集分布在搜索空间中的范围越广，种群的多样性越好。

2.3 NSGAII算法

       基于上述遗传算法和非支配排序技术，NSGAII算法通过不断地进化种群，找到多目标优化问题的最优解。NSGAII算法的主要流程如下：

（1）初始化种群：随机生成一组初始个体，并计算其适应度和拥挤度距离。

（2）选择操作：根据适应度函数和拥挤度距离对种群进行非支配排序，并选出一部分个体作为父代。

（3）交叉操作：对父代个体进行交叉操作，生成新的子代个体。

（4）变异操作：对子代个体进行变异操作，生成新的个体。

（5）合并种群：将父代和子代个体合并为一个种群。

（6）选择操作：根据适应度函数和拥挤度距离对种群进行非支配排序，并选出一部分个体作为下一代种群。

（7）终止条件：达到指定进化代数或找到满足停止条件的最优解，则终止算法。

2.4 优点

（1）能够有效地处理多目标优化问题，寻找多个最优解，而不是单个最优解。

（2）通过非支配排序技术，能够保持种群的多样性，避免种群陷入局部最优解。

（3）能够自适应地调整参数，根据问题的复杂度和搜索空间的大小自动调整进化算法的参数。

（4）易于实现和扩展，能够方便地应用于各种实际问题的求解。

2.5 缺点

（1）由于NSGAII算法采用遗传算法进行进化，因此在处理高维问题时，其搜索效率可能会受到影响。

（2）NSGAII算法需要大量的计算资源，特别是在处理复杂问题时，需要较长的计算时间。

（3）NSGAII算法在处理带有约束条件的多目标优化问题时，可能会遇到困难。

2.6 实现过程

NSGAII算法的实现过程可以分为以下几个步骤：

（1）定义问题：定义多个目标函数和约束条件，确定搜索空间的范围和问题的复杂度。

（2）初始化种群：随机生成一组初始个体，并计算其适应度和拥挤度距离。

（3）选择操作：根据适应度函数和拥挤度距离对种群进行非支配排序，并选出一部分个体作为父代。

（4）交叉操作：对父代个体进行交叉操作，生成新的子代个体。

（5）变异操作：对子代个体进行变异操作，生成新的个体。

（6）合并种群：将父代和子代个体合并为一个种群。

（7）选择操作：根据适应度函数和拥挤度距离对种群进行非支配排序，并选出一部分个体作为下一代种群。

（8）重复执行步骤（3）到（7），直到达到指定进化代数或找到满足停止条件的最优解。
        基于NSGAII的三目标优化算法是一种多目标优化算法，需要涉及到遗传算法、非支配排序技术、  多目标优化问题等专业点知识。具体来说，需要了解遗传算法的原理和操作，非支配排序技术的实现方法以及多目标优化问题的定义和求解方法。此外，还需要掌握MATLAB等工具的使用，实现基于NSGAII的三目标优化算法模型，进行实际问题的求解。基于NSGAII的三目标优化算法是一种有效的多目标优化算法，能够寻找多个最优解并保持种群的多样性。虽然该算法具有一些缺点，但在实际应用中已经被广泛使用，并取得了良好的效果。通过深入了解该算法的数学原理和实现方法，可以更好地应用于实际问题的求解，并为优化算法的研究提供参考。
 

二、核心程序

 
clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
rng('default') 
%初始化参数
popnum=200;
gen=600;
xmin=0;%变量取值范围
xmax=1;
m=2;%目标函数个数
n=30;%决策变量数目
hc=20;%交叉变异参数
hm=20;
%产生初始种群
initpop=rand(popnum,n)*(xmax-xmin)+xmin;
init_value_pop=value_objective(initpop,m,n);
%画图显示初始图
plot(init_value_pop(:,n+1),init_value_pop(:,n+m),'B+')
pause(.1)
%非支配排序和聚集距离计算
[non_dominant_sort_pop, rankinfo]=non_dominant_sort(init_value_pop,m,n);
ns_dc_pop=crowding_distance(non_dominant_sort_pop,m,n,rankinfo);
%选择，交叉，变异产生下一个子代
poolsize=round(popnum/2);%选择进行交叉变异的个数
toursize=2;%选择锦标赛的元度
select_pop=selection(ns_dc_pop,poolsize,toursize,m,n);
hc=20;%存储交叉变异相关参数
hm=20;
offspring=genetic_operate(select_pop,m,n,hc,hm,xmax,xmin);
%循环开始
t=1;
while t<=gen
t  
%合并种群(2N)，进入循环
combine_pop(1:popnum,1:m+n+2)=ns_dc_pop;
[xsize ysize]=size(offspring);
combine_pop(popnum+1:popnum+xsize,1:m+n+2)=offspring;
%重新进行非支配排序和聚焦距离计算
[gen_non_dominant_pop,rankinfo]=non_dominant_sort(combine_pop,m,n);
nsdc_pop=crowding_distance(gen_non_dominant_pop,m,n,rankinfo);
%选择下一代的产生（然后用于交叉变异）
ns_dc_pop=generate_offsprings(nsdc_pop,m,n,popnum);
 %显示下一代的情况
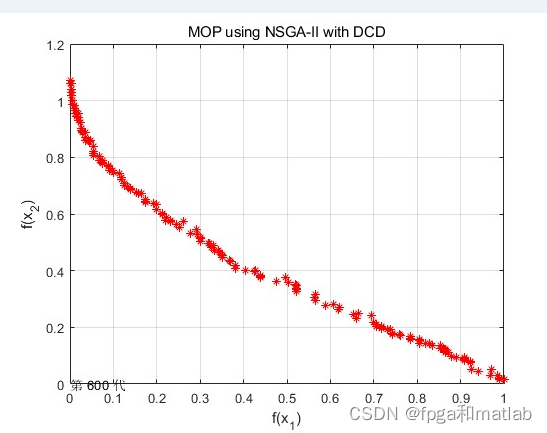
if m==2 
  plot(ns_dc_pop(:,n+1),ns_dc_pop(:,n+2),'r*')
elseif m==3  
    plot3(ns_dc_pop(:,n+1),ns_dc_pop(:,n+2),ns_dc_pop(:,n+3),'kd')  
    xlabel('Function 1');
    ylabel('Function 2');
    zlabel('Function 3');
end
 grid on;
text(0,0,0,['第 ',int2str(t),' 代']);
 pause(0.1)    
 %收敛性计算
 if t>=(gen*0.9)
     %导入标准解
     opt=load('paretoZDT1.dat');
     %得到函数解
   funcval=ns_dc_pop(:,n+1:n+m);  
   for j=1:m %求取最大最小值
       maxfval(j)=max(funcval(:,j));
       minfval(j)=min(funcval(:,j));
   end
   distance=zeros(1,size(funcval,1));
   sumfval=zeros(1,size(opt,1));
   dsum=0;
   for i=1:size(funcval,1)
      for j=1:size(opt,1)
        for k=1:m
          sumfval(j)= sumfval(j)+((funcval(i,k)-opt(j,k))/(maxfval(k)-minfval(k)))^2;
        end
      end
      distance(i)=sqrt(min(sumfval));
      sumfval(:)=0;
      dsum=dsum+distance(i);
   end   
     c=dsum/size(funcval,1)
 end 
%选择，交叉，变异产生下一个子代
poolsize=round(popnum/2);%选择进行交叉变异的个数
toursize=2;%选择锦标赛的元度
select_pop=selection(ns_dc_pop,poolsize,toursize,m,n);
hc=20;%存储交叉变异相关参数
hm=20;
offspring=genetic_operate(select_pop,m,n,hc,hm,xmax,xmin);
t=t+1;
end
%显示标题
        title('MOP using NSGA-II with DCD');
        xlabel('f(x_1)');
        ylabel('f(x_2)');

up2125

三、仿真结论