编译原理: Subset Construction 子集构造法(幂集构造)(NFA转DFA)

简介

上一篇：编译原理: Thompson 构造法（正则表达式 转 NFA）

我们再回顾一次使用正则表达式构建 DFA 的具体流程：

1. Thompson 构造法：正则表达式 RegExp -> 不确定有限状态机 NFA
2. 子集构造法：不确定有限状态机 NFA -> 确定有限状态机 DFA
3. 最小化：最小化确定有限状态机 DFA
4. 验证：DFA 转换为的等价正则表达式并验证等价

在前一篇我们完成了第一步构建出了 NFA，本篇将要使用子集构造法(Subset Construction)将 NFA 转换成 DFA。

本篇内容源于编译原理第二版(龙书)，直接看书搭配网上说明并动手实践是最清楚的。

参考

NFA转DFA的子集构造(subset construction)算法	https://www.jianshu.com/p/8e0fb9cf3f49
幂集构造-百度百科	https://baike.baidu.com/item/%E5%B9%82%E9%9B%86%E6%9E%84%E9%80%A0/22735892?fr=aladdin

正文

示例回顾

首先我们先来回顾以下上一篇使用 Thompson 构造法构造出的两个例子的 NFA

示例1: $a(b|c{)}^{\ast }$

示例2: $(a|b{)}^{\ast }abb$

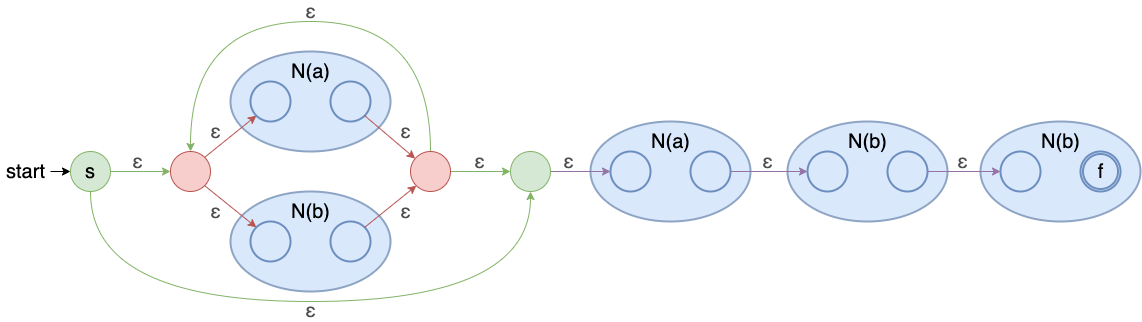
有了 NFA 你以为就可以了吗，那可不行。回顾上一篇说的 DFA 和 NFA 的差异，NFA 存在一个问题是对于同样的输入状态和输入字符，可能存在多个输出状态。

这可不行，这样我们在实际应用的时候怎么知道该往那个状态转移呢？所以我们就需要将 NFA 转换成 DFA 才方便后续的使用。

子集构造法 Subset Construction

接下来我们将使用子集构造法(Subset Construction，也称幂集构造)来将 NFA 转变成 DFA。

函数定义

在开始构建 DFA 之前，我们需要定义几个函数和状态的概念（以下提到的状态分为 DFA 状态和 NFA 状态，而 DFA 状态是一个 NFA 状态的集合。以下提到的状态除非特别说明否则默认指的是 NFA 状态）

1. $ϵ-closure(s),s\in S_{NFA}$ 闭包

• 输入：一个状态集 s
• 输出：所有 s 中的状态可经由任意长度的 $ϵ$ 边能抵达的状态集合
• 补充：这边的状态指的是 NFA 中的状态

2. $move(A,a),A\in S_{DFA},a\in \sum$

• 输入：一个 DFA 状态(即一个 NFA 的状态的集合，后续)，一个输入字符(a)
• 输出：DFA 状态中每个 NFA 状态透过 $a$ 边能抵达的所有 NFA 状态的集合

算法过程伪代码

接下来我们使用伪代码来描述子集构造法的构造过程

Subset-Construction(NFA)
    let Dtran be a table
    DFA_States = {ε-closure(NFA.s0)}  # DFA 状态集合的初始状态为 NFA 初始状态的闭包，并且未标记
    while (exist T in DFA_States not marked) { # 存在未标记的 DFA 状态
        mark T  # 标记 T，表示查过 T 状态的所有后续状态了
        for (a in Σ) { 
            Tc = ε-closure(move(T, a)) # 找到所有输入字符对应的下一个状态
            if (Tc not in DFA_States) { # 将状态加入到 DFA_States
                push Tc in DFA_States & unmarked Tc
            }
            Dtran[T, a] = Tc
        }
    }
    return Dtran

上面看起来很复杂，简单来说从起始状态开始($ϵ-closure(s0)$)，使用输入字符找到下一个 DFA 状态，并对于所有 DFA 状态递归搜索下一个状态知道成为闭包。

如果还是觉得很抽象不妨直接看向下面的示例吧！

构造 Dtran

上面 $Subset-Construction$ 的伪代码的最终目的就是要构建出一个 Dtran（同时就是 DFA 的一种表示）

接下来我们就分别对两个例子进行构建吧

示例1: $a(b|c{)}^{\ast }$

首先我们现对原来的 NFA 状态进行编号

1. 首先我们先求出起始 DFA 状态设为 $A$

A = ε-closure({a1}) = {a1}

这时候的 Dtran 状态如下

2. 第二步找到未标记状态 $A$，可输入字符为 $a$

Dtran[A,a] = ε-closure(move(A,a))
            = ε-closure({a2})
            = {a2,a3,a4,a5,a7,a10}

$Dtran[A,a]$ 表示的集合不在 Dtran 状态表里，则记为新状态 $B$

3. 下一个未标记状态为 $B$，可输入字符有 $b,c$

Dtran[B,b] = ε-closure(move(B,b))
           = ε-closure({a6})
           = {a4,a5,a6,a7,a9,a10}
           = C

Dtran[B,c] = ε-closure(move(B,c))
           = ε-closure({a8})
           = {a4,a5,a7,a8,a9,a10}
           = D

加入新状态 $C,D$

4. 下一个状态 $C$，可输入字符有 $b,c$

Dtran[C,b] = ε-closure(move(C,b))
           = ε-closure({a6})
           = {a4,a5,a6,a7,a9,a10}
           = C

Dtran[C,c] = ε-closure(move(C,c))
           = ε-closure({a8})
           = {a4,a5,a7,a8,a9,a10}
           = D

没有新状态，仅仅添加 $C$ 的输出状态

5. 下一个状态 $D$，可输入字符有 $b,c$

Dtran[D,b] = ε-closure(move(D,b))
           = ε-closure({a6})
           = {a4,a5,a6,a7,a9,a10}
           = C

Dtran[D,c] = ε-closure(move(D,c))
           = ε-closure({a8})
           = {a4,a5,a7,a8,a9,a10}
           = D

一样没有新状态，这时 $A,B,C,D$ 四个 DFA 状态形成了闭包，代表已经完成了最终 Dtran 表的构建了

示例2: $(a|b{)}^{\ast }abb$

第二个例子一样按照上面的顺序先编号后递归查找未标记状态对每个输入的输出状态，各个步骤的说明就省略了

1. 起始状态 $A$

A = ε-closure({b1}) = {b1,b2,b3,b5,b8,b9}

2. 状态 $A$，输入 $a,b$

Dtran[A,a] = ε-closure(move(A,a))
           = ε-closure({b4,b10})
           = {b2,b3,b4,b5,b7,b8,b9,b10,b11}
           = 新状态 B
           
Dtran[A,b] = ε-closure(move(A,b))
           = ε-closure({b6})
           = {b2,b3,b5,b6,b7,b8,b9}
           = 新状态 C

3. 状态 $B$，输入 $a,b$

Dtran[B,a] = ε-closure(move(B,a))
           = ε-closure({b4,b10})
           = {b2,b3,b4,b5,b7,b8,b9,b10,b11}
           = B
           
Dtran[B,b] = ε-closure(move(B,b))
           = ε-closure({b6,b12})
           = {b2,b3,b5,b6,b7,b8,b9,b12,b13}
           = 新状态 D

4. 状态 $C$，输入 $a,b$

Dtran[C,a] = ε-closure(move(C,a))
           = ε-closure({b4,b10})
           = {b2,b3,b4,b5,b7,b8,b9,b10,b11}
           = B
           
Dtran[C,b] = ε-closure(move(C,b))
           = ε-closure({b6})
           = {b2,b3,b5,b6,b7,b8,b9}
           = C

5. 状态 $D$，输入 $a,b$

Dtran[D,a] = ε-closure(move(D,a))
           = ε-closure({b4,b10})
           = {b2,b3,b4,b5,b7,b8,b9,b10,b11}
           = B
           
Dtran[D,b] = ε-closure(move(D,b))
           = ε-closure({b6,b14})
           = {b2,b3,b5,b6,b7,b8,b9,b14}
           = 新状态 E

6. 状态 $E$，输入 $a,b$

Dtran[E,a] = ε-closure(move(E,a))
           = ε-closure({b4,b10})
           = {b2,b3,b4,b5,b7,b8,b9,b10,b11}
           = B
           
Dtran[E,b] = ε-closure(move(E,b))
           = ε-closure({b6})
           = {b2,b3,b5,b6,b7,b8,b9}
           = C

绘制 DFA

其实到此我们已经完成 DFA 的构建了，Dtran 表就是一种也是应用时使用的 DFA 转换函数表，现在我们根据构建好的 Dtran 表绘制出对应的 DFA

示例1: $a(b|c{)}^{\ast }$

• Dtran 表

• DFA 图

示例2: $(a|b{)}^{\ast }abb$

• Dtran 表

• DFA 图

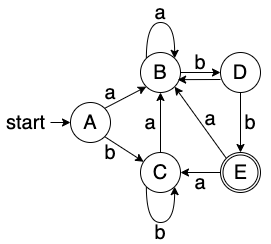
结语

到此我们已经成功的从正则表达式 -> NFA -> DFA，其实到现在这个步骤已经非常接近答案了，这个阶段构建出来的 DFA 也确实已经是能拿来使用了。下一篇我们将要介绍如何最小化 DFA 并且验证我们构建出来的 DFA 于原来的正则表达式等价。