微分方程的类型：

• 常微分方程
• 偏微分方程

常微分方程解法：

• 数值解
• 解析解

1.为什么非要用数值解的解法来解常微分方程呢？

是因为并不是所有常微分方程都可以写出原表达式，从而算出精确的解析解，所以我们只能用数值分析的方法去近似。
如下面这个常微分方程：
$$\frac{dy}{dx}=x\cdot y$$
我们是可以求出原函数的。
先将$y$除到左边来，$dx$乘到右边来，构造出两边都有微分项。
$$\frac{dy}{y}=xdx$$
然后两边同时积分：
$$\int \frac{dy}{y}=\int xdx$$
$$\ln |y|=\frac{1}{2}{x}^2+C$$
$$y=e^{\frac{1}{2}{x}^2+c}$$
之后我们要求这个微分方程的解就可以用这个解析式进行求解（代入一个初值之后求解）。

2.为什么必须要给出一个初始值才能求解呢？

因为求导会丢失掉函数的常数项部分的信息。
如：对$x^2$求导之后是$2x$，对$x^2+C$求导之后也是$2x$，所以求导之后就已经无法精确的知道原函数是什么了，所以需要一个初值来确定原函数中包含的常数项。

常微分方程数值解解法：

• 欧拉法
• 梯形欧拉法
• 龙格库塔法

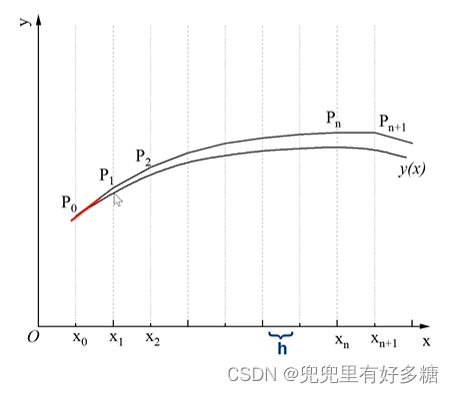
欧拉法

$$\begin{array}{l}\begin{array}{c}{y}^{\prime }=f(x,y),x\in \left[x_0,b\right]\end{array}\\ \\ \begin{array}{c}y\left(x_0\right)=y_0\end{array}\\ \\ \begin{array}{c}\frac{y_{n+1}-y_n}{x_{n+1}-x_n}=f\left(x_n,y_n\right)\end{array}\end{array}$$

对每个点做斜率，然后延长到下一个点，从而得出一条近似曲线就是上面画出的标P点的折线。即：欧拉法的主要思想就是用上面这条折线近似代替下面这条曲线。两个点之间的距离称作步长$h$。从而得到下式，就是欧拉法解微分方程的公式。

$$\begin{array}{c}{y}_{n+1}=y_n+hf\left(x_n,y_n\right)\end{array}$$

梯形欧拉法

梯形欧拉法是基于欧拉法进行改进的。
欧拉法中，$P_1$与$P_2$之间的斜率与$P_2$本身无关，只是从$P_1$处延伸过来的而已，而在梯形欧拉法中，就改进了这一点。
$P_2$处的斜率等于$P_2$与$P_1$处的斜率的算术平均。
即：
$$\frac{y_{n+1}-y_n}{x_{n+1}-x_n}=\frac{1}{2}\left(f\left(x_n,y_n\right)+f\left(x_{n+1},y_{n+1}\right)\right)$$
然后化简之后可得：
$$y_{n+1}=y_n+\frac{h}{2}\left(f\left(x_n,y_n\right)+f\left(x_{n+1},y_{n+1}\right)\right).$$

龙格库塔法

从上面的讲解可知，欧拉法是用前一个点或者后一个点的斜率来近似代表两点之间的斜率，梯形法用前后两点的斜率的算术平均值来代替两点之间的斜率，从而达到对曲线的近似。
而龙格库塔其本质其实也和上面的方法没有区别，是用更多的点的斜率来对两点之间的斜率进行近似。
$$y_{n+1}=y_n+hf\left(x_n+\theta h,y\left(x_n+\theta h\right)\right)$$
$$平均斜率：\bar{K}=f\left(x_n+\theta h,y\left(x_n+\theta h\right)\right)$$
通过取不同的$\theta$值，可以控制取多少个点。在两点之间取两个点，对其斜率算加权平均值就叫做二阶龙格库塔法；在两点之间取四个点，对其斜率算加权平均值就叫做四阶龙格库塔法。当然取的点数越多，精确度越高。
$$\{\begin{array}{l}{k}_1=f\left(x_n,y_n\right).\\ k_2=f\left(x_n+a_{1}h,y_n+h{b}_{21}{k}_1\right).\\ ⋮\\ k_r=f\left(x_n+a_{rh},y_n+h\cdot {\sum }_{j=1}^{r-1}{b}_{rj}{k}_j\right).\end{array}$$
$$\bar{k}=\sum _{i=1}^r{c}_i{k}_i$$

$$y_{n+1}=y_n+h\cdot \sum _{i=1}^l{w}_i{k}_i$$
展开来写是这样的：
$$y_{n+1}=y_n+h\sum _{i=1}^l{w}_i{y}_n^{\prime }\left(x_n+a_{i}h\right)$$
上式就很精准的表达了龙哥库塔法的精髓：就是取很多不同的点，算出其斜率，然后对每个斜率进行加权求和。只不过，加权的权值$w_i$和$k_i$并不是随便取的，取不同的权值会导致最后的精度不同，一般都是采用泰勒级数展开算出的权值，这种方法算出的权值可以使得近似精度最高，误差最小。
下面来证明一下龙格库塔法的系数来源：
我们假设$x_n$与$x_{n+1}$之间取了$i$个点，每个点是$x_n+a_{i}h$，$h$是步长，也就是每个点的间隔。当$a_1$规定为等于0，也就是$x_n+a_{1}h$等于$x_n$。那么第二个点就是$x_n+a_{2}h$，第三个点是$x_n+a_{3}h$，以此类推。
则有：
$$y_n^{\prime }\left(x_n+a_{1}h\right)=y_n^{\prime }\left(x_n\right)=f\left(x_n,y_n\right)=k_1$$
所以当我们忽略其他点，让$i$只能取1的时候，会发现式子就变成了欧拉法的样子，所以欧拉法其实是包含在龙哥库塔法中的。
同样的，当$i$取2的时候有：
$$\begin{array}{rl}{y}_n^{\prime }\left(x_n+a_{2}h\right)& =f\left(x_n+a_{2}h,y_n\left(x_n+a_{2}h\right)\right)\\ & =f\left(x_n+a_{2}h,y_n+a_{2}h{y}^{\prime }\left(x_n\right)\right)\\ & =f\left(x_n+a_{2}h,y_n+a_{2}hf\left(x_n{y}_n\right)\right)\\ & =f\left(x_n+a_{2}h,y_n+a_{2}h{k}_1\right)=k_2\end{array}$$
上面的推导中，从$y_n\left(x_n+a_{2}h\right)$到$y_n+a_{2}h{y}^{\prime }\left(x_n\right)$的变化可以看成是用欧拉法，也可以看作泰勒展开的前两项。
同样的当$i$取3的时候有:
$$\begin{array}{rl}{y}_n^{\prime }\left(x_n+a_{3}h\right)& =f\left(x_n+a_{3}h,y_n\left(x_n+a_{3}h\right)\right)\\ & =f\left(x_n+a_{3}h,y_n+a_{3}h\frac{b_{31}{y}^{\prime }\left(x_n\right)+b_{32}{y}^{\prime }\left(x_n+a_{2}h\right)}{\left(b_{31}+b_{32}\right)}\right)\\ & =f\left(x_n+a_{3}h,y_n+h\left(a_{31}{k}_1+a_{32}{k}_2\right)\right)=k_3\end{array}$$
我们最后可以得到：
$$\begin{array}{rl}& k_1=f\left(x_n,y_n\right)\\ & k_2=f\left(x_n+a_{2}h,y_n+a_{2}h{k}_1\right)\\ & k_3=f\left(x_n+a_{3}h,y_n+h\left(a_{31}{k}_1+a_{32}{k}_2\right)\right)\end{array}$$
从上面几个式子我们可以找规律，写出通式：
$$k_i=f\left(x_n+a_{i}h,y_n+h\sum _{\begin{array}{c}j=1\\ j<i\end{array}}^{\ell -1}{a}_{ij}{k}_j\right),i=1,2,\dots l$$
那么现在问题来了：这些式子中的参数$a_2$，$a_3$等等，如何求？谁决定这些参数？还有就是如何决定我们到底取几个点？算几次中间斜率？

下面我们先固定点数为2个，来解决这个问题：
Step1：
定义常微分方程：
$$y_{n+1}=y_n+h\left(w_1{k}_1+w_2{k}_2\right)$$
既然取两个点，那么中间的两个斜率分别为(为了方便，把变量替换为$\alpha$和$\beta$)：
$$\begin{array}{rl}{k}_1& =f\left(x_n,y_n\right)\\ k_2& =f\left(x_n+a_{2}h,y_n+h{a}_{21}{k}_1\right)\\ & =f\left(x_n+\alpha h,y_n+\beta h{k}_1\right)\end{array}$$
所以，目前一共有四个未知量等待解决：$w_1,w_2,\alpha ,\beta$。
我们使用泰勒展开来求解这几个未知量：
$$\begin{array}{rl}& y\left(x_{n+1}\right)=y\left(x_n\right)+h{y}^{\prime }\left(x_n\right)+\frac{h^2}{2!}{y}^{\prime \prime }\left(x_n\right)+\frac{h^3}{3!}{y}^{\prime \prime \prime }\left(x_n\right)+\cdots \\ & y^{\prime }\left(x_n\right)=f\left(x_n,y_n\right)\\ & y^{\prime \prime }\left(x_n\right)=[\frac{\partial f}{\partial x}+f(x,y)\frac{\partial f}{\partial y}]{|}_{\left(x_n,y_n\right)}\end{array}$$
$$y^{\prime \prime \prime }\left(x_n\right)=\frac{{\partial }^{2}f}{\partial x^2}+2f\frac{{\partial }^{2}f}{\partial x\partial y}+\frac{{\partial }^{2}f}{\partial y^2}+{\frac{\partial f}{\partial y}\left(\frac{\partial f}{\partial x}+f\frac{\partial f}{\partial y}\right)|}_{\left(x_n,y_n\right)}$$
然后我们将求得的斜率也做泰勒展开;
$$\begin{array}{rl}{k}_1=& f\left(x_n,y_n\right)\\ k_2=& f\left(x_n+\alpha h,y_n+\beta h{k}_1\right)\\ =& f\left(x_n,y_n\right)+\alpha h\frac{\partial f}{\partial x}+\beta h{k}_1\frac{\partial f}{\partial y}\\ & +\frac{1}{2!}\left({\alpha }^2{h}^2\frac{{\partial }^{2}f}{\partial x^2}+2\alpha \beta h^2{k}_1\frac{{\partial }^{2}f}{\partial x\partial y}+{\beta }^2{h}^2{k}_1^2\frac{{\partial }^{2}f}{\partial y^2}\right)\\ & +\dots .\end{array}$$
再带入原式中得：
$$\begin{array}{rl}{y}_{n+1}=& y_n+h{w}_1{k}_1+h{w}_2{k}_2\\ =& y_n+h{\omega }_{1}f+h{\omega }_2[f+h\left(\alpha \frac{\partial f}{\partial x}+\beta f\frac{\partial f}{\partial y}\right)\\ & +\frac{h^2}{2!}\left({\alpha }^2\frac{{\partial }^{2}f}{\partial x^2}+2\alpha \beta f\frac{{\partial }^{2}f}{\partial x\partial y}+{\beta }^2{f}^2\frac{{\partial }^{2}f}{\partial y^2}\right)+\cdot \cdot ]\end{array}$$
化简可得原式如下：
$$\begin{array}{rl}{y}_{n+1}\simeq & y_n+h\left(w_1+w_2\right)f+w_2{h}^2\left(\alpha \frac{\partial f}{\partial x}+\beta f\frac{\partial f}{\partial y}\right)\\ & +\frac{h^3}{2}{w}_2\left({\alpha }^2\frac{{\partial }^{2}f}{\partial x^2}+2\alpha \beta f\frac{{\partial }^{2}f}{\partial x\partial y}+{\beta }^2{f}^2\frac{{\partial }^{2}f}{\partial y^2}\right)+\cdots \end{array}$$
而$y_{n+1}$的泰勒展开如下：
$$\begin{array}{rl}y\left(x_{n+1}\right)=& y\left(x_n\right)+hf+\frac{h^2}{2}\left(\frac{\partial f}{\partial x}+f\frac{\partial f}{\partial y}\right)\\ & +\frac{h^3}{6}\left(\frac{{\partial }^{2}f}{\partial x^2}+2f\frac{{\partial }^{2}f}{\partial x\partial y}+\frac{{\partial }^{2}f}{\partial y^2}+\frac{\partial f}{\partial y}\left(\frac{\partial f}{\partial x}+f\frac{\partial f}{\partial y}\right)\right)\end{array}$$
将两个式子进行对比可得：
$$\begin{array}{rl}{w}_1+w_2& =1\\ \alpha w_2& =\frac{1}{2}\\ \beta w_2& =\frac{1}{2}\end{array}\}$$
此处共有四个未知数，但只有三个方程，所以我们只能通过一定的假设，获得他们之间的关系：
$$\begin{array}{rl}\alpha \ne 0,假设\beta & =\alpha ,\\ {\omega }_2& =\frac{1}{2\alpha }\\ {\omega }_1& =1-\frac{1}{2\alpha }\end{array}$$
那么原式就是：
$$\begin{array}{rl}& y_{n+1}\simeq y_n+h\left[\left(1-\frac{1}{2\alpha }\right)k_1+\frac{1}{2\alpha }{k}_2\right]\\ & k_1=f\left(x_n,y_n\right)\\ & k_2=f\left(x_n+\alpha h,y_n+\alpha h{k}_1\right)\end{array}$$
那么我们就可以通过给$\alpha$和$\beta $不同取值来探究哪一种取值能更精确的近似。
(i)
$$\begin{array}{rl}\text{if }\alpha =1/2& =\beta ;w_1=0,w_2=1\\ y_{n+1}& \simeq y_n+hf\left(x_n+\frac{h}{2},y_n+\frac{h}{2}f\right)\end{array}$$
(ii)
$$\begin{array}{rl}\alpha =1;\beta & =1,w_1=\frac{1}{2}=w_2\\ y_{n+1}& \simeq y_n+\frac{h}{2}\left(k_1+k_2\right)\\ k_1& =f\\ k_2& =f\left(x_n+\alpha h,y_n+\beta h{k}_1\right)\\ & =f\left(x_n+h,y_n+hf\right)\end{array}$$

MATLAB代码实例

实例1：

求解微分方程$\frac{dy}{dt}=-y+t+1$，$y_0=1$，$t$的取值是0到2，步长$h=0.1$，用欧拉法求解微分方程并将结果与$y(t)=e^{(-t)}+t$比较。

clear;
clc;
h=0.1;%初始化步长
y0=1;%给定的初值
t=0:h:2;%在0到2的区间内，以h为步长，初始化自变量
y=exp(-t)+t;%这个是解析解
n=length(t);%求一下自变量有多少个，来确定下面欧拉法的循环次数
numy=zeros(1,n);%将欧拉法的y值存储在一个行向量里边
dy=0;%第一个点的导数值是：-y0+t0+1=0 
numy(1)=y0;%向量的第一个值就是初值
for i=2:n
    numy(i)=y0+h*dy;%计算下一个值
    y0=numy(i);
    dy=-y0+t(i)+1;%计算当前点的斜率，作为这一点和下一点之间的近似斜率
end
figure;
plot(t,y,'r-',LineWidth=1);
hold on;
plot(t,numy,'b-',LineWidth=1);
xlabel('t');
grid on;
title('EUuler法求系统的输出响应');
ylabel('输出响应y(t)');
legend('解析解','Euler法');

实例2：

取h=0.01，采用欧拉法求解微分方程如下：
$$\{\begin{array}{c}\dot{y}(t)=y(t)-\frac{2t}{y(t)}0\le t\le 1\\ y(0)=1\end{array}$$
微分方程的解析解：
$$y(t)=\sqrt{1+2t}$$

clear;
clc;
h=0.01;
y0=1;
t=0:h:2;
y=sqrt(1+2*t);
n=length(t);
numy=zeros(1,n);
dy=1;%第一个点的导数值是：-y0+t0+1=0
numy(1)=y0;
for i=2:n
    numy(i)=y0+h*dy;
    y0=numy(i);
    dy=y0-2*t(i)/y0;
end
figure;
plot(t,y,'r-',LineWidth=1);
hold on;
plot(t,numy,'b-',LineWidth=1);
xlabel('t');
grid on;
title('EUuler法求系统的输出响应');
ylabel('输出响应y(t)');
legend('解析解','Euler法');

用梯形法改进后：

clear;
clc;
h=0.01;
y0=1;
t=0:h:2;
y=sqrt(1+2*t);
n=length(t);
numy=zeros(1,n);
dy=1;%第一个点的导数值是：-y0+t0+1=0
numy(1)=y0;
for i=2:n
    numy(i)=y0+h*dy;
    y1=numy(i);
    dy=1/2*(y1-2*t(i)/y1+y0-2*t(i-1)/y0);
    y0=y1;
end
figure;
plot(t,y,'r-',LineWidth=1);
hold on;
plot(t,numy,'b-',LineWidth=1);
xlabel('t');
grid on;
title('EUuler法求系统的输出响应');
ylabel('输出响应y(t)');
legend('解析解','Euler法');

实例3：

已知微分方程及初值如下所示，试比较在取不同步长时，其精确解与数值解之间的差异；
$$\{\begin{array}{ll}\dot{y}=-30y& \\ y(0)=\frac{1}{3}& 0\le t\le 1.5\end{array}$$
微分方程的解析解为：
$$y(t)=\frac{1}{3}{e}^{-30t}$$
代码：

%*************************h=0.1时曲线***************************************
clear
t(1)=0;                                         %设置自变量初值
y(1)=1/3;y_euler(1)=1/3;y_rk4(1)=1/3;           %设置解析解和数值解初值
h=0.1;                                          %设置计算步长

%求解析解
for k=1:15
    t(k+1)=t(k)+h;
    y(k+1)=exp(-30*t(k+1))/3;
end


%利用欧拉法求解
for k=1:15
    y_euler(k+1)=y_euler(k)+h*(-30*y_euler(k));
end


%利用RK4法求解
for k=1:15
    k1=-30*y_rk4(k);
    k2=-30*(y_rk4(k)+h*k1/2);
    k3=-30*(y_rk4(k)+h*k2/2);
    k4=-30*(y_rk4(k)+h*k3);
    y_rk4(k+1)=y_rk4(k)+h*(k1+2*k2+2*k3+k4)/6;
end

%绘制解析解的曲线图
plot(t,y);
legend('解析解, h=0.1');
grid on;


%绘制欧拉法的曲线图
plot(t,y_euler);
legend('欧拉法, h=0.1');
grid on;

%绘制RK4法的曲线图
plot(t,y_rk4);
legend('RK4法, h=0.1');
grid on;



%*************************h=0.075时曲线***************************************
clear
t(1)=0;                                         %设置自变量初值
y(1)=1/3;y_euler(1)=1/3;y_rk4(1)=1/3;           %设置解析解和数值解初值
h=0.075;                                        %设置计算步长

%求解析解
for k=1:20
    t(k+1)=t(k)+h;
    y(k+1)=exp(-30*t(k+1))/3;
end


%利用欧拉法求解
for k=1:20
    y_euler(k+1)=y_euler(k)+h*(-30*y_euler(k));
end


%利用RK4法求解
for k=1:20
    k1=-30*y_rk4(k);
    k2=-30*(y_rk4(k)+h*k1/2);
    k3=-30*(y_rk4(k)+h*k2/2);
    k4=-30*(y_rk4(k)+h*k3);
    y_rk4(k+1)=y_rk4(k)+h*(k1+2*k2+2*k3+k4)/6;
end

%绘制欧拉法的曲线图
plot(t,y_euler);
legend('欧拉法, h=0.075');
grid on;

%绘制RK4法的曲线图
plot(t,y_rk4);
legend('RK4法, h=0.075');
grid on;



%*************************h=0.05时曲线***************************************
clear
t(1)=0;                                         %设置自变量初值
y(1)=1/3;y_euler(1)=1/3;y_rk4(1)=1/3;           %设置解析解和数值解初值
h=0.05;                                         %设置计算步长

%求解析解
for k=1:30
    t(k+1)=t(k)+h;
    y(k+1)=exp(-30*t(k+1))/3;
end


%利用欧拉法求解
for k=1:30
    y_euler(k+1)=y_euler(k)+h*(-30*y_euler(k));
end


%利用RK4法求解
for k=1:30
    k1=-30*y_rk4(k);
    k2=-30*(y_rk4(k)+h*k1/2);
    k3=-30*(y_rk4(k)+h*k2/2);
    k4=-30*(y_rk4(k)+h*k3);
    y_rk4(k+1)=y_rk4(k)+h*(k1+2*k2+2*k3+k4)/6;
end

%绘制欧拉法的曲线图
plot(t,y_euler);
legend('欧拉法, h=0.05');
grid on;

%绘制RK4法的曲线图
plot(t,y_rk4);
legend('RK4法, h=0.05');
grid on;

%绘制解析解的曲线图
plot(t,y);
legend('解析解, h=0.05');
grid on;

在MATLAB中可以画出解析解的样子，可以看到，精确解单调下降并迅速收敛到0；

当h=0.1时，欧拉法和RK4法的解曲线均发散，仿真结果是错误的；

当h=0.075时，欧拉法的解曲线仍然发散，仿真结果是错误的；RK4法的解曲线单调下降并收敛到0，仿真结果是正确的


当h=0.05时，欧拉法和RK4法的解均收敛到0（虽然欧拉法的解曲线是振荡收敛的）。如果只要求得到t=1.5处的y(t)值，则两种数值积分算法的解都可以认为是正确的。

为什么会出现这种情况呢？这要涉及到计算稳定性的问题，这一点下一节再讲。