在计算机视觉中，有一个经典的变换被广泛使用——傅里叶变换。傅里叶变换是将时间域上的信号转变为频率域上的信号，进而进行图像去噪、图像增强等处理。

一、时域与频域

什么是时域（Time domain）？从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为，世间万物都在随着时间不停的改变，并且永远不会静止下来。

什么是频域（Frequency domain）？频域是描述信号在频率方面特性时用到的一种坐标系。用线性代数的语言就是装着正弦函数的空间。频域最重要的性质是：它不是真实的，而是一个数学构造。频域是一个遵循特定规则的数学范畴。正弦波是频域中唯一存在的波形，这是频域中最重要的规则，即正弦波是对频域的描述，因为时域中的任何波形都可用正弦波合成。

对于一个信号来说，信号强度随时间的变化规律就是时域特性，信号是由哪些单一频率的信号合成的就是频域特性。

时域分析与频域分析是对信号的两个观察面。时域分析是以时间轴为坐标表示动态信号的关系；频域分析是把信号变为以频率轴为坐标表示出来。一般来说，时域的表示较为形象与直观，频域分析则更为简练，剖析问题更为深刻和方便。目前，信号分析的趋势是从时域向频域发展。然而，它们是互相联系，缺一不可，相辅相成的。贯穿时域与频域的方法之一，就是传说中的傅里叶分析。傅里叶分析可分为傅里叶级数（Fourier Serie）和傅里叶变换(Fourier Transformation)。

二、傅里叶级数

傅里叶级数是一种对周期信号进行分解的方式。

如下图所示，左上角为正弦方波，余下为通过不同的正弦谐波数可以去拟合这个方波结果。

可以看到，叠加的谐波信号越多时，越接近于方波信号。

傅里叶级数由法国数学家傅里叶提出，即满足条件（狄利克雷条件）的任何周期函数可以由一系列不同频率的正弦（余弦）函数叠加而成。这种相加形式又称为级数，所以也称为傅里叶级数。

三、傅里叶变换

那么对信号的不同频率进行分解有什么好处呢？

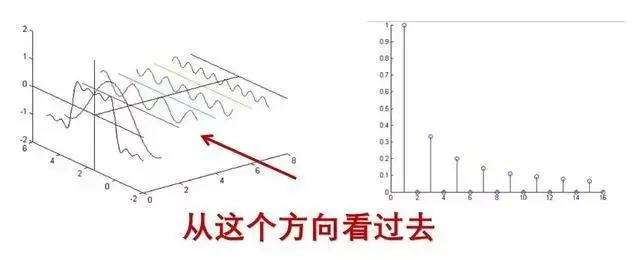
如下图所示，从时域上看，最下方叠加得到的信号是很难分析出里面蕴含的频率信息的。

而通过傅里叶分解后，如下图右图所示，可以很容易地观察到频率的有无和幅度的大小（相位也有对应的相位谱，这里没有列出）。

因此，通过傅里叶变换将某一信号分解为不同频率的信号，可以很容易地对信号中的某一段频段进行观察和操作。

3.1 傅里叶变换分类

根据原信号的不同类型，我们可以把傅立叶变换分为四种类别：

• 非周期性连续信号（傅立叶变换（Fourier Transform））
• 周期性连续信号（傅立叶级数(Fourier Series)）
• 非周期性离散信号（离散时域傅立叶变换（Discrete Time Fourier Transform））
• 周期性离散信号（离散傅立叶变换(Discrete Fourier Transform)）

这四种傅立叶变换都是针对正无穷大和负无穷大的信号，即信号的的长度是无穷大的，我们知道这对于计算机处理来说是不可能的，那么有没有针对长度有限的傅立叶变换呢？没有。因为正余弦波被定义成从负无穷小到正无穷大，我们无法把一个长度无限的信号组合成长度有限的信号。

面对这种困难，方法是把长度有限的信号表示成长度无限的信号，可以把信号无限地从左右进行延伸，延伸的部分用零来表示，这样，这个信号就可以被看成是非周期性离散信号，我们就可以用到离散时域傅立叶变换的方法。还有，也可以把信号用复制的方法进行延伸，这样信号就变成了周期性离散信号，这时我们就可以用离散傅立叶变换方法进行变换。

但是对于非周期性的信号，我们需要用无穷多不同频率的正弦曲线来表示，这对于计算机来说是不可能实现的，因为在计算机中只有离散的和有限长度的数据才能被处理。所以对于离散信号的变换只有离散傅立叶变换（DFT）才能被适用，对于其它的变换类型只有在数学演算中才能用到，在计算机中我们只能用DFT方法。

3.2 一维傅里叶公式

其中，ω 表示频率, t 表示时间, 它将频率域的函数表示为时间域函数 f(t) 的积分。

3.3 二维离散傅里叶变换

我们知道，灰度图像是由二维的离散的点构成的。二维离散傅里叶变换（Two-Dimensional Discrete Fourier Transform）常用于图像处理中，对图像进行傅里叶变换后得到其频谱图。频谱图中频率高低表征图像中灰度变化的剧烈程度。图像中边缘和噪声往往是高频信号，而图像背景往往是低频信号。我们在频率域内可以很方便地对图像的高频或低频信息进行操作，完成图像去噪，图像增强，图像边缘提取等操作。

对二维图像进行傅里叶变换公式如下：

其中，图像长 M，高 N。F(u,v)表示频域图像，f(x,y)表示时域图像。u 的范围为[0,M-1]，v 的范围为[0,N-1]。

对二维图像进行傅里叶逆变换公式如下：

其中，图像长 M，高 N。f(x,y)表示时域图像，F(u,v)表示频域图像。x 的范围为[0,M-1]，y 的范围为[0,N-1]。

四、OpenCV中傅里叶变换的应用

4.1 傅里叶变换

代码如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt
 
# 读取图像
img = cv2.imread('lenna.jpg', 0)
 
# 傅里叶变换
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
 
# 将频谱低频从左上角移动至中心位置
dft_shift = np.fft.fftshift(dft)
 
# 频谱图像双通道复数转换为0-255区间
result = 20*np.log(cv2.magnitude(dft_shift[:,:,0], dft_shift[:,:,1]))
 
# 显示图像
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(result, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

效果如下：

4.2 傅里叶逆变换

代码如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
img = cv2.imread('lenna.jpg', 0)
 
# 傅里叶变换
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
dftshift = np.fft.fftshift(dft)
res1= 20*np.log(cv2.magnitude(dftshift[:,:,0], dftshift[:,:,1]))
 
# 傅里叶逆变换
ishift = np.fft.ifftshift(dftshift)
iimg = cv2.idft(ishift)
res2 = cv2.magnitude(iimg[:,:,0], iimg[:,:,1])
 
# 显示图像
plt.subplot(131), plt.imshow(img, 'gray'), plt.title('Original Image')
plt.axis('off')
plt.subplot(132), plt.imshow(res1, 'gray'), plt.title('Fourier Image')
plt.axis('off')
plt.subplot(133), plt.imshow(res2, 'gray'), plt.title('Inverse Fourier Image')
plt.axis('off')
plt.show()

效果如下：

源码仓库地址

🌼图像处理、机器学习的常用算法汇总