点乘与叉乘是线性代数的基本知识，在工作中也经常能够遇到，下面我们来温习一下它们的概念以及使用C++代码对它们进行实现。

1. 点乘

• 概念

向量的点乘，也叫点积、内积、数量积。是指在实数R上的两个向量的一种二元运算，这种运算返回一个实数值标量。点乘有两种定义方式：代数方式和几何方式。

• 代数方式

已知两个向量$\overrightarrow{a}=[a_1,a_2,...,a_n]$和$\overrightarrow{b}=[b_1,b_2,...,b_n]$，则向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的内积代数定义为：
$$a\cdot b=a_1{b}_1+a_2{b}_2+...+a_n{b}_n$$
代数表示：对应元素相乘相加。

• 几何定义(2维和3维)

已知两个向量$\overrightarrow{a}=[x_1,y_1,z_1]$和$\overrightarrow{b}=[x_2,y_2,z_2]$，它们的模值分别为$|a|$和$|b|$，它们的夹角为$\theta \in [0,\pi ]$，那么向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的几何定义为：
$$a\cdot b=|a||b|cos\theta$$
几何意义： 可以用来表示一个向量在另一个向量上的投影长度，为一个标量。

2. 叉乘

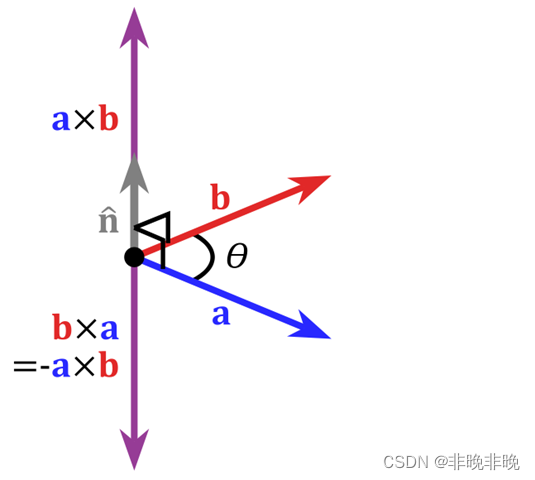
向量的叉乘，也叫叉积、外积、向量积，是一种在向量空间中(也就是说向量元素个数为3)向量的二元运算。与点积不同，叉乘的运算结果是一个向量而不是一个标量，并且两个向量的叉积与这两个向量所构成的平面垂直。

• 定义方式

已知两个向量$\overrightarrow{a}=[x_1,y_1,z_1]$和$\overrightarrow{b}=[x_2,y_2,z_2]$，它们的模值分别为$|a|$和$|b|$，它们的夹角为$\theta \in [0,\pi ]$，那么向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的叉乘表示为：

• 模值：$|a\times b|=\mid a\mid \mid b\mid sin\theta$
• 模的几何意义：模$|a\times b|$, 即以a和b为两条边的平行四边形的面积
• 方向：两个向量的叉积与这两个向量所构成的平面垂直，且遵循右手准则（右手的四指从a以不超过180°的转角转向b时，竖起的大拇指指向是叉乘的方向。）

• 坐标运算

假设：$i、j、k$分别为XYZ三个轴的单位向量，则叉乘运算表示如下：

$$\overrightarrow{a}\times \overrightarrow{b}=\left|\begin{array}{ccc}i& j& k\\ x_1& y_1& z_1\\ x_2& y_2& z_2\end{array}\right|=[y_1{z}_2-y_2{z}_1,-(x_1{z}_2-x_2{z}_1),x_1{y}_2-x_2{y}_1]$$

特殊情况，如果a和b在平面XY上，那么Z=0，所以上面得到的值$|x_1{y}_2-x_2{y}_1|$，方向朝Z轴。

3. 代码实现

根据对上面概念的理解，相信大家可以很快就能写出自己的点乘与叉乘函数操作，这里就不介绍了。在工作实际应用中，我们可能更多的使用Eigen对它们进行调用，Eigen可以很方便的实现点乘与叉乘操作，具体代码如下：

#include <iostream>
#include <Eigen/Dense>
 
using namespace Eigen;
using namespace std;
int main()
{
  Vector3d v(1,2,3);
  Vector3d w(0,1,2);
 
  cout << "Dot product: " << v.dot(w) << endl;//点乘
  double dp = v.adjoint()*w; //等同于点法
  cout << "Dot product via a matrix product: " << dp << endl;
  cout << "Cross product:\n" << v.cross(w) << endl;//叉乘
}

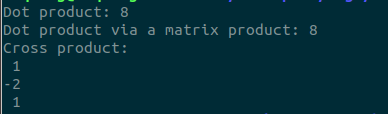
输出：