AES加密解密算法
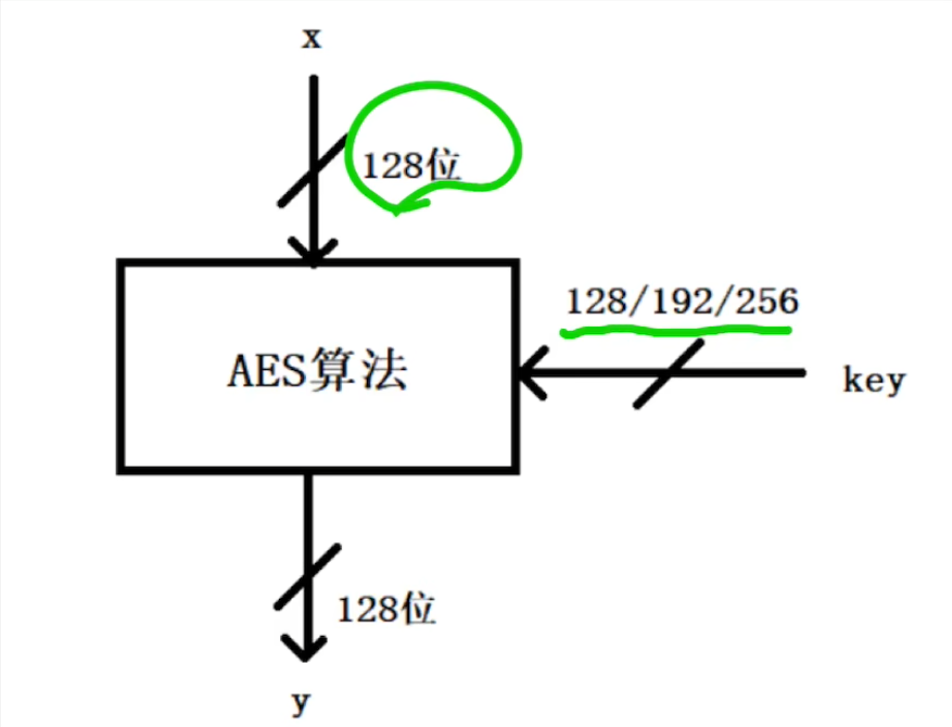
AES属于分组加密,算法明文长度固定为128位(单位是比特bit,1bit就是1位,128位等于16字节)而密钥长度可以是128、192、256位当密钥为128位时,需要循环10轮完成加密,在此基础上,密钥每增加64位,就要多循环2轮(即192位密钥循环12轮,256位密钥循环14轮)
一,AES算法概述
AES属于分组加密,算法明文长度固定为128位(单位是比特bit,1bit就是1位,128位等于16字节)
而密钥长度可以是128、192、256位
当密钥为128位时,需要循环10轮完成加密,在此基础上,密钥每增加64位,就要多循环2轮(即192位密钥循环12轮,256位密钥循环14轮)

二,加密过程
(零)加密过程总览
以128位密钥为例子,AES算法会对明文先进行【初始变换】(这里的初始变换不属于10轮加密的范畴内),然后是9轮【循环运算】,加1轮【最终轮】,最终得到密文
这里的最终轮其实唯一的区别就是最终轮少了9轮主循环中第3步的列混合

(一)初始变换
首先要理解,无论是明文还是密钥,16个字节(即128位)的字符,在进行加密的过程中都是以4*4的矩阵形式存在的,这个矩阵也有要求——输入的字符需要按从上到下从左往右的顺序排列成矩阵

接受了这个概念后,我们来看AES的初始变换操作,其实十分简单,就是对明文矩阵和密钥矩阵对应的元素异或得到新矩阵,如下图

(二)9轮循环运算
(1)字节代换
对于完成第一步初始变换的矩阵进行字节代换
我们要将矩阵中的每一个元素都替换掉,但替换是有规则的替换,即S-BOX,按照矩阵元素的值去映射S-BOX中对应的值

(2)行移位
对于完成字节替换的矩阵进行行移位
规则是矩阵的第一行不变,第二行向左移动1个字节,第三行向左移动2个字节,第四行向左移动3个字节
注意,这里认为矩阵的最左边连通最右边,即坐标(2,1)的p2左移后出现在坐标(2,4)

下图是步骤(1)字节替换后的矩阵进行行移位的结果

(3)列混合(该操作在最终轮不执行)
对于完成行移位的矩阵进行列混合
规则是左乘一个给定的4*4矩阵,注意这个矩阵是程序设计时给定的,可能每个程序使用的AES算法中的这个矩阵不一定相同
(注意,这里的矩阵乘法并不是简单的线性代数中的元素相乘相加,本篇不展开讲,详见本篇->关于AES的列混合计算和解密流程问题_aes列混合运算-CSDN博客)

下图是步骤(2)行移位后的矩阵进行列混合的结果

(4)轮密钥加
对于完成列混合的矩阵进行轮密钥加
规则是对完成列混合的矩阵和轮密钥矩阵对应的元素进行异或,这里我们先知道要这样操作即可,至于轮密钥矩阵在后面马上就介绍了

(*)轮密钥矩阵
最开始只有一个密钥矩阵(假设就是下图这个矩阵),我们对这个矩阵的列进行如下标号
9轮循环运算中,每进行一轮,需要对密钥拓展出如下图的ai列,并使(a1, a2, a3, ai)成为当前轮的轮密钥矩阵


拓展时,使用如下规则——
- 如果i不是4的倍数,那么第i列由如下等式确定:a[i]=a[i-4] ^ a[i-1],例如i等于5时:a[i]=a[1] ^ a[4],即第2列和第5列异或(第1轮没有第5列,第2轮才有第5列)
- 如果i是4的倍数,那么第i列由如下等式确定:a[i]=a[i-4]^T(a[i-1]),例如i等于4时,a[i]=a[0] ^ T(a[3]),即第1列和经过T函数计算的第4列异或
函数T由3部分组成:字循环、字节代换和轮常量异或(坚持一下,就要结束了┭┮﹏┭┮)
①字循环
下图是对i等于4的情况下进行字循环操作

②字节代换
和9轮循环运算中的第(1)步操作是一样的,将字节映射到进行的S-BOX中进行字节替换

③轮常量异或
轮常量是给定的,这里的Rcon就是轮常量矩阵,可能每个程序使用的AES算法中的这个矩阵不一定相同
(注意,下图左,橙色列和黄色列是轮常量异或,最终再异或蓝色列是按照公式a[i]=a[i-4]^T(a[i-1])拓展轮密钥矩阵,蓝色列就是公式中的a[i-4])

(补充),AES加密的不同模式
AES加密算法的模式主要有五种,它们是ECB模式、CBC模式、CFB模式、OFB模式和CTR模式。它们之间的主要区别在于加密过程中明文和密文的处理方式以及安全性特点:
ECB模式:
- 每个明文块被独立加密,相同的明文块得到相同的密文块。
- 不适合加密大量数据或具有重复模式的数据,容易受到攻击。
CBC模式:
- 使用前一个密文块对当前明文块进行加密,增加了随机性,相同的明文块在不同位置得到不同密文块。
- 需要使用初始化向量(IV)来增加安全性。
CFB模式:
- 使用前一个密文块作为输入生成伪随机密钥流与明文进行异或运算得到密文。
- 可以支持实时加密和流加密。
OFB模式:
- 类似于CFB,使用前一个密文块生成伪随机密钥流,然后与明文进行异或运算。
- 对加密和解密中的错误更加鲁棒,但不支持部分更新。
CTR模式:
- 使用一个计数器与密钥输入加密算法生成伪随机密钥流,与明文进行异或运算。
- 可以并行加密和解密,适用于需要高效加密的场景。
选择哪种模式取决于具体应用的需求和安全性要求,例如需要实时加密或流加密的场景可选用CFB模式,而需要高效加密的场景可选用CTR模式。
三,实际运用
博主最近在钻研逆向技术,在逆向分析过程中会遇到AES加密,因此需要略微了解AES算法的原理(深入了解就是密码学者干的事情了,逆向分析但求能一眼看出是AES加密即可)
如下图,在第31行运用到了AES加密(当然这题属于十分基础的,函数名直接表明是AES加密了)

在函数中此函数中,能够很清晰地看出AES的循环加密过程

知道它是AES加密后,逆向的工作就很清楚了,我们只需要从程序中分析获取密文和密钥,解密即可获得flag,至于解密的具体代码不必关心,可以直接借助python的第三方库解决,会写脚本即可
(这里只做举例,具体问题请具体分析)
from Crypto.Cipher import AES
#注意解密过程中密钥的格式需要为byte类型,字符串转byte直接在开头加个b标志
key = b'1234567890123456'
#注意解密过程中密文的格式需要为byte类型,本题获取到的是十六进制文本,处理成字符串后使用bytes.fromhex()函数转为对应的字节数组
en_text = bytes.fromhex('F3498AED82CE44E2357C23F5DCF897A43B6A7BFEE0467C591E301CBC38F99913')
aes = AES.new(key, AES.MODE_ECB) #创建一个AES解密对象,需要传入密钥和加密模式(这里是ECB模式)
print(aes.decrypt(en_text)) #调用decrypt方法实现解密

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容






所有评论(0)