1. 动态规划简介

1.1 什么是动态规划

动态规划（Dynamic programming），是一种在数学、计算机科学和经济学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划算法通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。

动态规划对于子问题重叠的情况特别有效，因为它将子问题的解保存在表格中，当需要某个子问题的解时，直接取值即可，从而避免重复计算。

动态规划是一种灵活的方法，不存在一种万能的动态规划算法可以解决各类最优化问题（每种算法都有它的缺陷）。所以除了要对基本概念和方法正确理解外，必须具体问题具体分析处理，用灵活的方法建立数学模型，用创造性的技巧去求解。

1.2 基本策略

动态规划中的子问题往往不是相互独立的（即子问题重叠）。在求解的过程中，许多子问题的解被反复地使用。为了避免重复计算，动态规划算法采用了填表来保存子问题解的方法。

动态规划与分治法类似，都是把大问题拆分成小问题，通过寻找大问题与小问题的递推关系，解决一个个小问题，最终达到解决原问题的效果。但不同的是，分治法在子问题和子子问题等上被重复计算了很多次，而动态规划则具有记忆性，通过填写表把所有已经解决的子问题答案记录下来，在新问题里需要用到的子问题可以直接提取，避免了重复计算，从而节约了时间，所以在问题满足最优性原理之后，用动态规划解决问题的核心就在于填表，表填写完毕，最优解也就找到。

最优性原理是动态规划的基础，最优性原理是指“多阶段决策过程的最优决策序列具有这样的性质：不论初始状态和初始决策如何，对于前面决策所造成的某一状态而言，其后各阶段的决策序列必须构成最优策略”。

1.3 适用问题及求解步骤

那么什么样的问题适合用动态规划的方法来解决呢？适合用动态规划来解决的问题，都具有下面三个特点：最优化原理、无后效性、有重叠子问题。

（1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

（2）无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

（3）有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势。

这类问题的求解步骤通常是：初始状态→│决策1│→│决策2│→…→│决策n│→结束状态。具体包括以下几步：

（1）划分：按照问题的特征，把问题分为若干阶段。注意：划分后的阶段一定是有序的或者可排序的。

（2）确定状态和状态变量：将问题发展到各个阶段时所处的各种不同的客观情况表现出来。状态的选择要满足无后续性。

（3）确定决策并写出状态转移方程：状态转移就是根据上一阶段的决策和状态来导出本阶段的状态。根据相邻两个阶段状态之间的联系来确定决策方法和状态转移方程。

（4）边界条件：状态转移方程是一个递推式，因此需要找到递推终止的条件。

1.4 算法实现

动态规划三要素：

（1）问题的阶段

（2）每个阶段的状态

（3）相邻两个阶段之间的递推关系

整个求解过程可以用一张最优决策表来描述，最优决策表是一张二维表（行：决策阶段，列：问题的状态）。表格需要填写的数据一般对应此问题在某个阶段某个状态下的最优值（如最短路径，最长公共子序列，最大价值等），填表的过程就是根据递推关系，最后根据整个表格的数据通过简单的取舍或者运算求得问题的最优解。

2. 01背包问题

2.1 问题描述

有n个物品，它们有各自的体积和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值总和？假设给定背包容量为8，物品信息如下表所示：

i（物品编号）	1	2	3	4
w（体积）	2	3	4	5
v（价值）	3	4	5	6

2.2 总体思路

根据动态规划解题步骤（问题抽象化、建立模型、寻找约束条件、判断是否满足最优性原理、找大问题与小问题的递推关系式、填表、寻找解组成）找出01背包问题的最优解以及解组成，然后编写代码实现。

2.3 解决过程

0、在解决问题之前，为描述方便，首先定义一些变量：capacity表示背包总容量，Vi表示第 i 个物品的价值，Wi表示第 i 个物品的体积，定义V(i,j)：当前背包容量 j，前 i 个物品最佳组合对应的价值。同时，将背包问题抽象化（X1，X2，…，Xn，其中 Xi 取0或1，表示第 i 个物品选或不选）。

1、建立模型，即求max(V1X1+V2X2+…+VnXn)；

2、寻找约束条件，W1X1+W2X2+…+WnXn<capacity；

3、寻找递推关系式，面对当前商品有两种可能性：

• 包的容量比该商品体积小，装不下，此时的价值与前i-1个的价值是一样的，即V(i,j)=V(i-1,j)；
• 还有足够的容量可以装该商品，但装了也不一定达到当前最优价值，所以在装与不装之间选择最优的一个，即V(i,j)=max｛V(i-1,j)，V(i-1,j-w(i))+v(i)｝。
  其中V(i-1,j)表示不装，V(i-1,j-w(i))+v(i) 表示装了第i个商品，背包容量减少w(i)，但价值增加了v(i)。

由此可以得出递推关系式：
$$\{\begin{array}{ll}j<w(i)& V(i,j)=V(i-1,j)\\ j>=w(i)& V(i,j)=max｛V(i-1,j)，V(i-1,j-w(i))+v(i)｝\end{array}$$

这里需要解释一下，为什么能装的情况下，需要这样求解（这是本问题的关键所在）。可以这么理解，如果要到达 V(i,j) 这一个状态有几种方式？

肯定是两种，第一种是第i件商品没有装进去，第二种是第i件商品装进去了。没有装进去很好理解，就是V(i-1,j)；装进去了怎么理解呢？如果装进去第i件商品，那么装入之前是什么状态，肯定是V(i-1,j-w(i))。由于最优性原理（上文讲到），V(i-1,j-w(i))就是前面决策造成的一种状态，后面的决策就要构成最优策略。两种情况进行比较，得出最优。

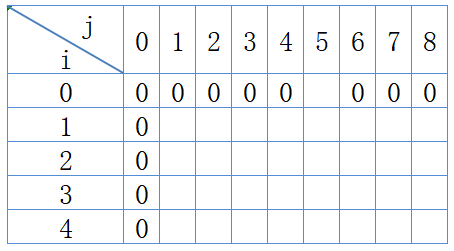
4、填表，首先初始化边界条件，V(0,j)=V(i,0)=0；

然后一行一行的填表：

如，i=1，j=1，w(1)=2，v(1)=3，有j<w(1)，故V(1,1)=V(1-1,1)=0；
又如，i=1，j=2，w(1)=2，v(1)=3，有j=w(1)，故V(1,2)=max｛ V(1-1,2)，V(1-1,2-w(1))+v(1) ｝=max｛0，0+3｝=3；
如此下去，填到最后一个，i=4，j=8，w(4)=5，v(4)=6，有j>w(4)，故V(4,8)=max｛ V(4-1,8)，V(4-1,8-w(4))+v(4) ｝=max｛9，4+6｝=10。

所以填完表如下图：

5、表格填完，最优解即是V(number,capacity)=V(4,8)=10。

2.4 代码实现

// C风格输入
#include <iostream>
#include <algorithm>
 
int main() {
	int w[5] = { 0 , 2 , 3 , 4 , 5 }; // 商品的体积2、3、4、5，0留空
	int v[5] = { 0 , 3 , 4 , 5 , 6 }; // 商品的价值3、4、5、6，0留空
	int dp[5][9] = { 0 }; // 动态规划表
 
	for (int i = 1; i <= 4; ++i) {
		for (int j = 1; j <= 8; ++j) {
			if (j < w[i])
				dp[i][j] = dp[i - 1][j];
			else
				dp[i][j] = std::max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
		}
	}
 
	// 动态规划表的输出
	for (int i = 0; i < 5; ++i) {
		for (int j = 0; j < 9; ++j) {
			std::cout << dp[i][j] << ' ';
		}
		std::cout << std::endl;
	}
 
	return 0;
}

// C++风格输入
#include <iostream>
#include <vector>
#include <algorithm>
 
int main() {
	std::vector<int> w = { 0 , 2 , 3 , 4 , 5 }; // 商品的体积2、3、4、5，0留空
	std::vector<int> v = { 0 , 3 , 4 , 5 , 6 }; // 商品的价值3、4、5、6，0留空
	std::vector<std::vector<int>> dp(5);   // 动态规划表
	for (int i = 0; i < dp.size(); ++i)
        dp[i].resize(9);
 
	for (int i = 1; i <= 4; ++i) {
		for (int j = 1; j <= 8; ++j) {
			if (j < w[i])
				dp[i][j] = dp[i - 1][j];
			else
				dp[i][j] = std::max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
		}
	}
 
	// 动态规划表的输出
	for (int i = 0; i < 5; ++i) {
		for (int j = 0; j < 9; ++j) {
			std::cout << dp[i][j] << ' ';
		}
		std::cout << std::endl;
	}
 
	return 0;
}

2.5 最优解回溯

通过上面的方法可以求出背包问题的最优解，但还不知道这个最优解由哪些商品组成，故要根据最优解回溯找出解的组成，根据填表的原理可以有如下的寻解方式：

• V(i,j)=V(i-1,j)时，说明没有选择第i 个商品，则回到V(i-1,j)；
• V(i,j)=V(i-1,j-w(i))+v(i)时，说明装了第i个商品，该商品是最优解组成的一部分，随后我们得回到装该商品之前，即回到V(i-1,j-w(i))，一直遍历到i＝0结束为止，所有解的组成都会找到。

具体如下：

• 最优解为V(4,8)=10，而V(4,8)!=V(3,8)，V(4,8)=V(3,8-w(4))+v(4)=V(3,3)+6=4+6=10，所以第4件商品被选中，并且回到V(3,8-w(4))=V(3,3)；
• 有V(3,3)=V(2,3)=4，所以第3件商品没被选择，回到V(2,3)；
• 而V(2,3)!=V(1,3)，V(2,3)=V(1,3-w(2))+v(2)=V(1,0)+4=0+4=4，所以第2件商品被选中，并且回到V(1,3-w(2))=V(1,0)；
• 有V(1,0)=V(0,0)=0，所以第1件商品没被选择。

代码如下：

#include <iostream>
#include <algorithm>

int w[5] = { 0 , 2 , 3 , 4 , 5 }; // 商品的体积2、3、4、5，0留空
int v[5] = { 0 , 3 , 4 , 5 , 6 }; // 商品的价值3、4、5、6，0留空
int dp[5][9] = { 0 }; // 动态规划表
int item[5]; // 最优解情况

// 最优解回溯
void findWhat(int i, int j) {				
	if (i >= 0) {
		if (dp[i][j] == dp[i - 1][j]) {
			item[i] = 0;
			findWhat(i - 1, j);
		} else if (dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
			item[i] = 1;
			findWhat(i - 1, j - w[i]);
		}
	}
}

int main() {
	// 动态规划算法
	for (int i = 1; i <= 4; ++i) {
		for (int j = 1; j <= 8; ++j) {
			if (j < w[i])
				dp[i][j] = dp[i - 1][j];
			else
				dp[i][j] = std::max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
		}
	}
 
	// 动态规划表的输出
	for (int i = 0; i < 5; ++i) {
		for (int j = 0; j < 9; ++j) {
			std::cout << dp[i][j] << ' ';
		}
		std::cout << std::endl;
	}

	findWhat(4, 8);
	// 输出最优解
	for (int i = 0; i < 5; ++i)			
		std::cout << item[i] << ' ';
	std::cout << std::endl;
	
	return 0;
}