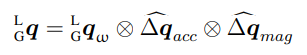
IMU 互补滤波器
本文主要介绍《Keeping a Good Attitude: A Quaternion-Based OrientationFilter for IMUs and MARGs》一文的互补滤波算法论文下载地址https://www.mdpi.com/1424-8220/15/8/19302,文中带了基础知识的讲解,比较全面。如果下载不到,可尝试使用https://download.csdn.net/
本文主要介绍《Keeping a Good Attitude: A Quaternion-Based Orientation
Filter for IMUs and MARGs》一文的互补滤波算法
论文下载地址https://www.mdpi.com/1424-8220/15/8/19302,文中带了基础知识的讲解,比较全面。
如果下载不到,可尝试使用https://download.csdn.net/download/weixin_41469272/15005220
源代码使用介绍:http://wiki.ros.org/imu_tools
源代码(C++)地址:https://github.com/ccny-ros-pkg/imu_tools
1 算法介绍
使用imu数据,解析获得姿态角。作者是基于四元数的解析运算。
算法主要思路:使用陀螺仪输出的角加速度,积分获得角度。然后通过加速度计的输出,修正该角度的滚转角和俯仰角;最后通过磁力计修正偏航角。

算法框图:
- 当imu数据只有三轴加速度计和3轴陀螺仪,即输出只有3轴线加速度和3轴角速度

- 当imu数据只有三轴加速度计、3轴陀螺仪、以及磁力计

2 算法实现
2.1 陀螺仪角速度预积分
本文一律使用四元数来表述旋转,离散系统下的第k时刻的姿态角四元数可通过下式计算获得:
G
L
q
w
,
t
k
=
G
L
q
t
k
−
1
+
G
L
q
˙
w
,
t
k
Δ
t
^L_Gq_{w,t_k}= ^L_Gq_{t_{k-1}} + ^L_G\dot q_{w,t_k} \Delta t
GLqw,tk=GLqtk−1+GLq˙w,tkΔt
其中,G代表世界坐标系,L代表当前坐标系(body坐标系)
G
L
q
w
,
t
k
^L_Gq_{w,t_k}
GLqw,tk乘以一个向量,可将该向量从世界坐标系旋转到当前坐标系。
G
L
q
˙
w
,
t
k
^L_G\dot q_{w,t_{k}}
GLq˙w,tk表示k时刻时,四元数的导数。
四元数的导数计算公式:

使用前向差分计算
G
L
q
˙
w
,
t
k
^L_G\dot q_{w,t_{k}}
GLq˙w,tk:

圈乘的公式定义:

将圈乘化为普通的点乘运算:


2.2 加速度计线加速度修正
使用2.1角速度得到的 G L q w , t k ^L_Gq_{w,t_k} GLqw,tk,将3轴线加速度转换到世界坐标系下,利用转换后的世界坐标系下的加速度(合加速度单位化为1),与真值 [ 0 , 0 , 1 ] T [0,0,1]^T [0,0,1]T(重力加速度)对比,得到 Δ q a c c \Delta q_{acc} Δqacc。
由于利用3轴线加速度数据,只能计算出滚转角及俯仰角,因此 Δ q a c c \Delta q_{acc} Δqacc只包含滚转角和俯仰角的修正。
因为偏航角,不会改变加速度计的读数,详见https://www.zhihu.com/question/68156189解释。
-
利用陀螺仪得到的 G L q w {^L_Gq_w} GLqw,将 L a {^La} La转换到世界坐标系下:
R ( L G q w ) L a = G g p = R ( G L q w ∗ ) L a R(^G_Lq_w){^La}={^Gg_p}=R(^L_Gq^*_w){^La} R(LGqw)La=Ggp=R(GLqw∗)La
与该文章保持一致, G L q w ∗ {^L_Gq^*_w} GLqw∗表示 ( L G q w ) (^G_Lq_w) (LGqw)反变换四元数。 -
将第一步得到的世界坐标系下加速度的估算 G g p {^Gg_p} Ggp,和实际的重力加速度作对比。计算出 G L q w {^L_Gq_w} GLqw的误差四元数:

R ( q ) R(q) R(q)表示四元数q对应的旋转矩阵,具体公式如下:

整理得:

关于四元数求解,上述方程为欠定方程,作者认为,上述方程有唯一的滚转角和俯仰角,但是任意的偏航角,为得到确定的解,因此,作者令 Δ q a c c = 0 \Delta q_{acc}=0 Δqacc=0,最后解得:

该解有一个奇点,当 g z = − 1 g_z=-1 gz=−1,由于 g z g_z gz接近1,因此这个解可以使用,如果更严格的公式,需使用文章中的公式(25)分段解。

-
加速度计解算四元数修正
由于加速度计含有高频噪声,尤其是在高动态情况下,加速度计会受其他外力的影响,因此,需要对该解算进行滤波:
作者通过在0值四元数和 Δ q a c c \Delta q_{acc} Δqacc之间线性插值并标准化,得到最后的修正四元数:
当 Δ q 0 a c c > ϵ \Delta q_{0acc}>\epsilon Δq0acc>ϵ时,即旋转角度接近0时,使用线性插值法如下:此时

当 Δ q 0 a c c < = ϵ \Delta q_{0acc}<=\epsilon Δq0acc<=ϵ时,使用球面插值法,如下:

其中: q I q_I qI为旋转角为0的四元数

其中的 α \alpha α值,需要根据物体的高动态情况来做调整。
1)当物体运动处于运动高动态时,加速度计的输出就不够准确,但是陀螺仪的输出所受物体高动态的镜像较小,因此高动态时,增大陀螺仪角度的权重,减少加速度计的影响。即使 α \alpha α接近0。
2)当物体长时间静止时,陀螺仪的静差等会产生累积误差,但是加速度计对角度的计算在物体静止时,比较准确,因此,需要增大加速度计计算的角度影响,即使 α \alpha α接近1。
当 α \alpha α接近1,采用加速度数据计算的角度。
当 α \alpha α接近0,采用陀螺仪数据得到的角度。
这里的高通和低通的概念并不明显。
通过以下方法计算 α \alpha α:

其中, ∣ ∣ L α ~ ∣ ∣ ||^L \widetilde{\alpha} || ∣∣Lα ∣∣表示物体加速度总和。 e m e_m em越大,表明除重力加速度之外,物体受的其他外力越大,加速度结果得到的角度不准确。此时:

α ‾ \overline{\alpha} α为常数项, f ( e m ) f(e_m) f(em)为gain factor。f函数:
-
叠加 Δ q ^ a c c \widehat{\Delta q}_{acc} Δq acc

关于普通线性插值和球面插值的区别:也可参考四元数球面插值

2.3 磁力计修正
由于加速度计只能修正滚转角和偏航角,采用磁力计修正偏航角。
磁力计的输出可以理解为磁线与机体坐标系3轴夹角的表彰或者投影。
- 利用线加速度修正后得到的
G
L
q
′
{^L_Gq'}
GLq′将磁力计数据转换到中间坐标系下:
该中间坐标系与世界坐标系z轴一致,但是x,y轴不确定(因为经过加速度计不能修正偏航角)。

- 再计算
Δ
q
m
\Delta q_m
Δqm使
l
l
l可以转到世界坐标系下,其中我们定义世界坐标系的
x
x
x轴指向北极,即,世界坐标系下的磁极线处在xz平面上,y轴上数据为0。得:

世界坐标系与中间坐标系之间转换只差偏航角运动。因此,令:

整理得:

解得:

*修正加速度修正后的姿态,加入偏航角修正:

3 其他算法
其实上述方法个人测试挺实用的,但是文中对互补滤波的部分并不明显。有其他互补滤波的算法,通过过滤加速度计的高频干扰和陀螺仪的低频干扰,最后叠加得到姿态角。
原理解释:
-
加速度计对加速度比较敏感,取瞬时值计算倾角误差比较大;加速度计测倾角,其动态响应较慢,在高频时信号不可用,所以可通过低通抑制高频;
-
陀螺仪积分得到的角度不受加速度的影响,但是随着时间的增加积分漂移和温度漂移带来的误差比较大。陀螺响应快,积分后可测倾角,不过由于零漂等,在低频段信号不好。
-
互补滤波就是在短时间内采用陀螺仪得到的角度做为最优,定时对加速度采样来的角度进行取平均值来校正陀螺仪的得到的角度。就是,短时间内用陀螺仪比较准确,以它为主;长时间用加速度计比较准确,这时候加大它的比重。
加速度计要滤掉高频信号,陀螺仪要滤掉低频信号,互补滤波器就是根据传感器特性不同,通过不同的滤波器(高通或低通,互补的),然后再相加得到整个频带的信号。
通过高通滤波可抑制低频噪声。将两者结合,就将陀螺和加表的优点融合起来,得到在高频和低频都较好的信号,互补滤波需要选择切换的频率点,即高通和低通的频率。
鉴于加速度计低频特性比较好,因为加速度的角度可以直接算出来,没有累积误差,所以长时间后也比较准。而陀螺仪长时间后由于积分误差的累加,会造成输出误差比较大,甚至无法使用。所以用互补滤波法根据他们的特性取长补短进行姿态解算,每过一段时间就让加速度计去校准一下陀螺仪。互补滤波就是在短时间内采用陀螺仪得到的角度做为最优值,定时对加速度采样来的加速度值进行取平均值来校正陀螺仪的得到的角度。短时间内用陀螺仪比较准确,以它为主;长时间用加速度计比较准确,这时候加大它的比重,这就是互补了,不过加速度计要滤掉高频信号,陀螺仪要滤掉低频信号,互补滤波器就是根据传感器特性不同,通过不同的滤波器(高通或低通,互补的),然后再相加得到整个频带的信号。互补是给他们不同的权重加权求和。–来自参考链接3
互补滤波器:

加速度计数据输入给低通滤波,当输入频率大于截止频率
1
/
τ
1/\tau
1/τ时,输出幅值大幅度减少,相位延迟增大;陀螺仪数据输入给高通滤波,当输入频率小于截止频率
1
/
τ
1/\tau
1/τ时,输出幅值大幅度减少,相位超前;看Bode图示例:
τ
=
1
\tau=1
τ=1,红线为低通滤波器,黄线为高通滤波器。
trick:一阶高通滤波分子有s,一阶低通滤波分子无s,因为有s会超前相位,增大幅值。

以上部分来自参考链接1
参考链接
https://zhuanlan.zhihu.com/p/108101458
https://blog.csdn.net/Gen_Ye/article/details/52522721?locationNum=10
https://blog.csdn.net/superrunner_wujin/article/details/55809648

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献14条内容
已为社区贡献14条内容





所有评论(0)