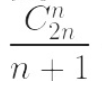
数据结构 | 算法中的卡特兰数的应用
输入一个整数n,计算h(n)。令h(0)=1,h(1)=1,Catalan数满足递推式例如另类递推式递推关系的解为递推关系的另类解为//函数功能计算Catalan的第n项//函数参数n为项数//返回值第n个Catalan数{return1;//保存临时结果//h(0)和h(1)i...
卡特兰数又称卡塔兰数,卡特兰数是组合数学中一个常出现在各种计数问题中出现的数列。
一、简单介绍

输入一个整数n,计算h(n)。
令h(0)=1,h(1)=1,
Catalan数满足递推式:h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)
例如:
h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
另类递推式:h(n)=h(n-1)*(4*n-2)/(n+1);
递推关系的解为:h(n)=C(2n,n)/(n+1) (n=0,1,2,...)
递推关系的另类解为:h(n)=C(2n,n)-C(2n,n+1)(n=0,1,2,...)
直接根据递归式,写出相应的算法:
//函数功能: 计算Catalan的第n项
//函数参数: n为项数
//返回值: 第n个Catalan数
int Catalan(int n)
{
if(n <= 1)
return 1;
int *h = new int [n+1]; //保存临时结果
h[0] = h[1] = 1; //h(0)和h(1)
for(int i = 2; i <= n; i++) //依次计算h(2),h(3)...h(n)
{
h[i] = 0;
for(int j = 0; j < i; j++) //根据递归式计算 h(i)= h(0)*h(i-1)+h(1)*h(i-2) + ... + h(i-1)h(0)
h[i] += (h[j] * h[i-1-j]);
}
int result = h[n]; //保存结果
delete [] h; //注意释放空间
return result;
}
二、卡特兰数的应用
应用1:出栈次序。(进出栈问题)
【问题描述】
一个栈(无穷大)的进栈序列为1,2,3,…,n,出栈顺序种数h(n)为多少?
【问题分析】
常规分析
首先,我们设f(n)=序列个数为n的出栈序列种数。同时,我们假定,从开始到栈第一次出到空为止,这段过程中第一个出栈的序数是k。特别地,如果栈直到整个过程结束时才空,则k=n。首次出空之前第一个出栈的序数k将1~n的序列分成两个序列,其中一个是1~k-1,序列个数为k-1,另外一个是k+1~n,序列个数是n-k。此时,我们若把k视为确定一个序数,那么根据乘法原理,f(n)的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数,即选择k这个序数的f(n)=f(k-1)×f(n-k)。而k可以选1到n,所以再根据加法原理,将k取不同值的序列种数相加,得到的总序列种数为:f(n)=f(0)f(n-1)+f(1)f(n-2)+……+f(n-1)f(0)。看到此处,再看看卡特兰数的递推式,答案不言而喻,即为f(n)=h(n)= C(2n,n)/(n+1)= c(2n,n)-c(2n,n+1)(n=0,1,2,……)。最后,令f(0)=1,f(1)=1。
非常规分析
对于每一个数来说,必须进栈一次、出栈一次。我们把进栈设为状态‘1’,出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b),因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数的方案种数。在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求(由左而右扫描,0的累计数大于1的累计数)的方案数即为所求。
不符合要求的数的特征是由左而右扫描时,必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数,此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换,使之成为n-m个0和n-m-1个1,结果得1个由n+1个0和n-1个1组成的2n位数,即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。反过来,任何一个由n+1个0和n-1个1组成的2n位二进制数,由于0的个数多2个,2n为偶数,故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换,使之成为由n个0和n个1组成的2n位数,即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。因而不合要求的2n位数与n+1个0,n-1个1组成的排列一一对应。
显然,不符合要求的方案数为c(2n,n+1)。由此得出输出序列的总数目=c(2n,n)-c(2n,n+1)=c(2n,n)/(n+1)=h(n)。
应用2:括号匹配
【问题描述】
由1对括号,可以组成一种合法括号序列:()。
由2对括号,可以组成两种合法括号序列:()()、(())。
由n对括号组成的合法括号序列一共有多少种?
【问题分析】
思路:n对括号相当于有2n个符号,n个左括号、n个右括号,可以设问题的解为f(2n)。第0个符号肯定为左括号,与之匹配的右括号必须为第2i+1字符。因为如果是第2i个字符,那么第0个字符与第2i个字符间包含奇数个字符,而奇数个字符是无法构成匹配的。
通过简单分析,f(2n)可以转化如下的递推式 f(2n) = f(0)*f(2n-2) + f(2)*f(2n - 4) + ... + f(2n - 4)*f(2) + f(2n-2)*f(0)。简单解释一下,f(0) * f(2n-2)表示第0个字符与第1个字符匹配,同时剩余字符分成两个部分,一部分为0个字符,另一部分为2n-2个字符,然后对这两部分求解。f(2)*f(2n-4)表示第0个字符与第3个字符匹配,同时剩余字符分成两个部分,一部分为2个字符,另一部分为2n-4个字符。依次类推。
假设f(0) = 1,计算一下开始几项,f(2) = 1, f(4) = 2, f(6) = 5。结合递归式,不难发现f(2n) 等于h(n)。
应用3:矩阵链乘
【问题描述】
矩阵链乘: P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?h(n-1)
【问题分析】
思路:可以这样考虑,首先通过括号化,将P分成两个部分,然后分别对两个部分进行括号化。比如分成(a1)×(a2×a3.....×an),然后再对(a1)和(a2×a3.....×an)分别括号化;又如分成(a1×a2)×(a3.....×an),然后再对(a1×a2)和(a3.....×an)括号化。
设n个矩阵的括号化方案的种数为f(n),那么问题的解为
f(n) = f(1)*f(n-1) + f(2)*f(n-2) + f(3)*f(n-3) + f(n-1)*f(1)。f(1)*f(n-1)表示分成(a1)×(a2×a3.....×an)两部分,然后分别括号化。
计算开始几项,f(1) = 1, f(2) = 1, f(3) = 2, f(4) = 5。结合递归式,不难发现f(n)等于h(n-1)。
应用4:二叉树生成问题
【问题描述】
n个节点构成的二叉树,共有多少种情形?h(n)
【问题分析】
思路一:可以这样考虑,根肯定会占用一个结点,那么剩余的n-1个结点可以有如下的分配方式,T(0, n-1),T(1, n-2),...T(n-1, 0),设T(i, j)表示根的左子树含i个结点,右子树含j个结点。
设问题的解为f(n),那么f(n) = f(0)*f(n-1) + f(1)*f(n-2) + .......+ f(n-2)*f(1) + f(n-1)*f(0)。假设f(0) = 1,那么f(1) = 1, f(2) = 2, f(3) = 5。结合递推式,不难发现f(n)等于h(n)。
思路二:假设采用中序遍历,根节点第k个被访问,则根的左子树共有k-1个结点,右子树共有n-k个结点,k同样可以取1-n,这就与进出栈问题分析思路一致了,所以一共h(n)种。
应用5:满二叉树个数
【问题描述】
n+1个叶子的满二叉树个数为多少?
【问题分析】
不再分析,答案为h(n)。
应用6:圆划分问题
【问题描述】
在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?h(n)
【问题分析】
思路:以其中一个点为基点,编号为0,然后按顺时针方向将其他点依次编号。那么与编号为0相连点的编号一定是奇数,否则,这两个编号间含有奇数个点,势必会有个点被孤立,即在一条线段的两侧分别有一个孤立点,从而导致两线段相交。设选中的基点为A,与它连接的点为B,那么A和B将所有点分成两个部分,一部分位于A、B的左边,另一部分位于A、B的右边。然后分别对这两部分求解即可。
设问题的解f(n),那么f(n) = f(0)*f(n-2) + f(2)*f(n-4) + f(4)*f(n-6) + ......f(n-4)*f(2) + f(n-2)*f(0)。f(0)*f(n-2)表示编号0的点与编号1的点相连,此时位于它们右边的点的个数为0,而位于它们左边的点为2n-2。依次类推。
f(0) = 1, f(2) = 1, f(4) = 2。结合递归式,不难发现f(2n) 等于h(n)。
应用7:凸多边形三角形划分
【问题描述】
一个凸的n边形,用直线连接它的两个顶点使之分成多个三角形,每条直线不能相交,问一共多少种方案? 比如凸六边形的划分情况为:
 h(6)=14。
h(6)=14。
【问题分析】
我们将凸多边形顶点从p1一直编号到pn,以p1pn这条边为基准,任选一个数k(2<=k<=n-1),将p1,pk以及pn三点连接,构成了一个三角形。该三角形把该凸边形划分成了两个凸边形,一边顶点为1 ~ k-1,另一边为k+1 ~ n,于是又回到了进出栈问题,所以答案依旧为:h(n)。
应用8:排队方式
【问题描述】
有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?
【问题分析】
思路:可以将持5元买票视为进栈,那么持10元买票视为5元的出栈。这个问题就转化成了栈的出栈次序数。由应用2的分析直接得到结果,f(2n) 等于h(n)。
PS应用8:游乐园门票1元一张,每人限购一张。现在有10个小朋友排队购票,其中5个小朋友每人只有1元的钞票一张,另5个小朋友每人只有2元的钞票一张,售票员没有准备零钱。问:有多少种排队方法,使售票员总能找的开零钱?
答:现把拿1元的5个小朋友看成是相同的,把拿2元的5个小朋友也看成是相同的,使用我们常用的“逐点累加法”:
图中每条小横段表示拿1元的小朋友,每条小竖段表示拿2元的小朋友,要求从A走到B的过程中网格中任何点均有横段数不小于竖段数:拿1元的要先,且人数不能少于拿2元的,即不能越过对角线AB:每个点所标的数即为从A走到此点的方法数。求从A到B的走法的方法数。逐点累加可求出为42,即卡特兰数C5=42。
又由于每个小朋友是不相同的,所以共有42×5!×5!=42×120×120=604800种情况。
若把此题的10个人,拿1元的有5人,拿2元的有5人改为共有2n个人,拿1元的n人,拿2元的n人,则符合要求的排队方法数为:n!*n!*h(n)=n!*n!*C(2n,n)/(n+1)=(2n)!/(n+1)
应用9:填充问题
【问题描述】
n个长方形填充一个高度为n的阶梯状图像方法数为多少?
【问题分析】
答案为h(n)。
三、卡特兰数的实例
组合数学中有非常多的组合结构可以用卡塔兰数来计数。在Richard P. Stanley的Enumerative Combinatorics: Volume 2一书的习题中包括了66个相异的可由卡塔兰数表达的组合结构。以下用Cn=3和Cn=4举若干例:
例1.Cn表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串,且所有的前缀字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words: h(3)=5
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY
例2.将上例的X换成左括号,Y换成右括号,Cn表示所有包含n组括号的合法运算式的个数:h(3)=5
((())) ()(()) ()()() (())() (()())
例3.Cn表示有n个节点组成不同构二叉树的方案数。下图中n等于3,圆形表示节点,月牙形表示什么都没有。h(3)=5
例4.Cn表示所有在n × n格点中不越过对角线的单调路径的个数。一个单调路径从格点左下角出发,在格点右上角结束,每一步均为向上或向右。计算这种路径的个数等价于计算Dyck word的个数: X代表“向右”,Y代表“向上”。下图为n = 4的情况:h(4)=14
类似:一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?h(n)
例5.Cn表示通过连结顶点而将n边的凸多边形分成三角形的方法个数。下图中为n=6的情况:h(n-2)=h(4)=14
例6.Cn表示用n个长方形填充一个高度为n的阶梯状图形的方法个数。下图为 n = 4的情况:h(4)=14
例7.进栈出栈问题:
饭后,姐姐洗碗,妹妹把姐姐洗过的碗一个一个放进碗橱摞成一摞。一共有n个不同的碗,洗前也是摞成一摞的,也许因为小妹贪玩而使碗拿进碗橱不及时,姐姐则把洗过的碗摞在旁边,问:小妹摞起的碗有多少种可能的方式?h(n)
一个汽车队在狭窄的路面上行驶,不得超车,但可以进入一个死胡同去加油,然后再插队行驶,共有n辆汽车,问共有多少种不同的方式使得车队开出城去?h(n)
【408统考】先序序列为a,b,c,d 的不同二叉树的个数是 () 。
【解析】
前序序列和中序序列的关系相当于以前序序列为入栈次序,以中序序列为出栈次序。
转化为“以序列a, b, c, d为入栈次序,则出栈序列的个数为多少”。
对于n个不同元素进栈,出栈序列的个数为
卡特兰数的应用:![]()
总结参考于

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献12条内容
已为社区贡献12条内容







所有评论(0)