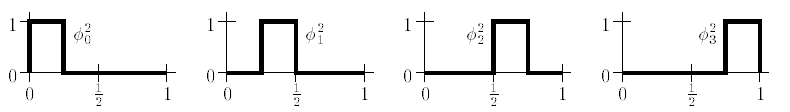
【滤波·4】Haar小波——原理
本系列文章尽量以便于理解的方式讲解 Haar 小波的原理和应用。其中应用部分主要关注于 PRT 中使用的 double product integral 和 triple product integral 两部分。主要参考文献为 Stollnitz et al. 的 Wavelets for Computer Graphics: A Primer 和 Ren Ng 的两篇 wavelet reli
本系列文章尽量以便于理解的方式讲解 Haar 小波的原理和应用。其中应用部分主要关注于 PRT 中使用的 double product integral 和 triple product integral 两部分。 主要参考文献为 Stollnitz et al. 的 Wavelets for Computer Graphics: A Primer 和 Ren Ng 的两篇 wavelet relighting 的经典文章。
1. 1D Haar
Haar 小波是最简单的小波基函数。
我们首先从一个一维的 Haar 小波分解的例子开始:
假设我们有一张一维的“图像”,它的分辨率是 1 x 4:
[8,4,1,3]
可以用如下方法,将这张图像用一维 Haar 小波系数表示:
(1)计算两两像素之间的均值
[8+42,1+32]=[6,2]
(2)计算两两像素之间的差值
[8−42,1−32]=[2,−1]
这样我们就对原来的图像进行了一次 Haar 分解。每经过一次分解,均值“图像”的分辨率就会减半。对每次产生的新的均值部分重复上面两个步骤,直到均值只剩下一个数,无法进一步分解:
| Resolution | 均值(Approximation coefficients) | 差值(Detail coefficients) |
|---|---|---|
| 4 | [8, 4, 1, 3] | |
| 2 | [6, 2] | [2, -1] |
| 1 | [4] | [2] |
这样,我们就得到了一组由 1 个均值(approximation coefficients)和 3 个差值(detail coefficients)组成的 Haar 小波基系数:
[8,4,1,3]→[4,2,2,−1]
在这个分解过程中,图像信息没有任何损失,通过分解的逆操作可以无损地还原图像:
[4,2,2,−1]→[4+2,4−2,2,−1]=[6,2,2,−1]
[6,2,2,−1]→[6+2,6−2,2+(−1),2−(−1)]=[8,4,1,3]
上面的还原方法是基于我们进行分解的逆操作得到的,接下来我们从基函数的角度来看刚刚的分解和还原过程。
首先介绍 Haar 小波的两个函数。


从基函数的角度看之前的分解过程

经过第一次分解得到的系数是 [6,2,2,−1], 其中 approximation coefficients 是 6,2,detail coefficients 是 2,−1 ,对应表达式为:

经过第二次分解得到的系数是 [4,2,2,−1], 其中 approximation coefficients 是 4,detail coefficients 是 2,2,−1:

2. 2D Haar
2D Haar 分解可以看作分别对所有行和所有列进行 1D Haar 分解。根据不同顺序分解行和列会产生两种不同的分解方法。
先把行分解到最精细,然后再分解列的方法叫做 standard decomposition。而行列交替分解的方法叫做 non-standard decomposition。

Standard decomposition

Non-standard decomposition
需要注意的是,这两种分解方法所产生的基函数是不一样的,要加以区分。
在后面我们要介绍的 triple Product Wavelet Integrals 所用到的是第二种 non-standard decomposition。
3. 小波实例
// verified on opencv4.2.0
# include<opencv.hpp>
# include<iostream>
using namespace std;
using namespace cv;
int main()
{
Mat img = imread("Lena.jpg", cv::IMREAD_GRAYSCALE);
int width = img.cols;
int height = img.rows;
int depth = 2;
int depthcount = 1;
Mat tmp = Mat::ones(img.size(), CV_32FC1);
Mat wavelet = Mat::ones(img.size(), CV_32FC1);
Mat imgtmp = img.clone();
imshow("src", imgtmp);
imgtmp.convertTo(imgtmp, CV_32FC1, 1.0 / 255);
while (depthcount <= depth)
{
height = img.rows / depthcount;
width = img.cols / depthcount;
//calculate horizen
for (int i = 0; i < height; i++) //row
{
for (int j = 0; j < width / 2; j++) // col
{
tmp.at<float>(i, j) = (imgtmp.at<float>(i, 2 * j) + imgtmp.at<float>(i, 2 * j + 1)) / 2; //mean
tmp.at<float>(i, j + width / 2) = (imgtmp.at<float>(i, 2 * j) - imgtmp.at<float>(i, 2 * j + 1)) / 2; //diff
}
}
// calculate vertical
for (int i = 0; i < height / 2; i++)
{
for (int j = 0; j < width; j++)
{
wavelet.at<float>(i, j) = (tmp.at<float>(2 * i, j) + tmp.at<float>(2 * i + 1, j)) / 2;
wavelet.at<float>(i + height / 2, j) = (tmp.at<float>(2 * i, j) - tmp.at<float>(2 * i + 1, j)) / 2;
}
}
imgtmp = wavelet;
depthcount++;
}
normalize(wavelet, wavelet, 0, 1, cv::NORM_MINMAX);
imshow("wavelet", wavelet);
waitKey(0);
return 0;
}Reference
Wavelets for Computer Graphics: A Primer

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献27条内容
已为社区贡献27条内容







所有评论(0)