---

引言

交通分布预测是交通需求预测四阶段模型的第二步，是把交通的发生与吸引量预测的各小区的发生与吸引量转换成各小区之间的空间 OD 量，即 OD 矩阵。因此本章主要讲述交通规划中分布交通量预测的基本概念、理论模型及其应用，主要包括增长系数法和重力模型法的原理、模型结构、算法、参数标定以及介入机会模型和最大熵模型的概要等。

大纲要求是理解概念和模型，掌握增长系数法模型及重力模型法及参数标定。

一、概述

交通分布中最基本的概念之一是 OD 表，O 表示出发点 (Origin) ，D 表示目的地 (Destination)。交通分布通常用一个 2 维矩阵表示。一个小区数为 $n$ 的区域的 OD 表，一般表示为下表所示形式。

表中，$q_{ij}$ 为以小区 $i$ 为起点、小区 $j$ 为终点的交通量；$O_i$ 为小区 $i$ 的发生交通量；$D_j$ 为小区 $j$ 的吸引交通量；$T$ 为研究对象区域的生成交通量。

对此 OD 表，下面各式所示守恒法则成立：$$\sum _j{q}_{ij}=O_i,\sum _i{q}_{ij}=D_j,\sum _i\sum _j{q}_{ij}=\sum _i{O}_i=\sum _j{D}_j=T\text{\hspace{1em}(1)}$$ 分布交通量预测要解决的问题是在目标年各交通小区的发生与吸引交通量一定的条件下，求出各交通小区之间将来的 OD 交通量。求得的 OD 交通量也是一个 2 维 OD 表，也同样要满足 (1) 式的约束条件。分布交通量预测是交通规划的主要步骤之一，是交通设施规划和交通政策制订不可缺少的资料。

分布交通量的预测方法一般可以分为两类：一类是增长系数法，一类是综合法。前者假定将来 OD 交通量的分布形式和现有的 OD 表的分布形式相同，在此假定的基础上预测对象区域目标年的 OD 交通量，常用的方法包括常增长系数法、平均增长系数法、底特律法 (Detroit)、福莱特 (Fratar) 法、佛尼斯法 (Furness) 法等；后者从分布交通量的实际分析中，剖析 OD 交通量的分布规律，并将此规律用数学模型表现，然后用实测数据标定模型参数，最后用标定的模型预测分布交通量，其方法包括重力模型法、介入机会模型法、最大熵模型法等。

由上述可知，增长系数法的应用前提是要求被预测区域有完整的现状 OD 表。对于综合法来说，如果模型已经标定完毕，则不需要现状 OD 表。当然，一般来说，模型参数的标定需要对象区域的实际数据，也就是说 OD 表还是需要的。然而，此种情况即使没有完整的 OD 表也可以进行模型参数的标定。因此，同增长系数法相比，综合法的应用范围更广，但对于模型的标定有一定的难度，特别是介入机会模型和最大熵模型，在实际规划中不常使用。

二、增长系数法

2.1 模型与算法

在分布交通量预测中，增长系数法的原理是，假设在现状分布交通量给定的情况下，预测将来的分布交通量。

增长系数法的算法步骤为：

步骤一：令计算次数 $m=0$。

步骤二：给定现状 OD 表中 $q_{ij}^m,O_i^m,D_j^m,T^m$ 及将来 OD 表中的 $U_i,V_j,X$。

步骤三：求出各小区的发生与吸引交通量的增长率 $F_{O_i}^m,F_{D_j}^m$。$$F_{O_i}^m=U_i/O_i^m,F_{D_j}^m=V_j/D_j^m$$ 步骤四：求第 $m+1$ 次分布交通量的近似值 $q_{ij}^{m+1}$。$$q_{ij}^{m+1}=q_{ij}^m\cdot f(F_{O_i}^m,F_{D_j}^m)$$ 步骤五：收敛判别。$$\begin{gathered} O_i^{m+1}=\sum _j{q}_{ij}^{m+1},D_j^{m+1}=\sum _i{q}_{ij}^{m+1} \\ 1-ϵ<F_{O_i}^{m+1}=U_i/O_i^{m+1}<1+ϵ \\ 1-ϵ<F_{D_j}^{m+1}=U_i/D_j^{m+1}<1+ϵ \end{gathered}$$ 式中，$U_i$ 为将来 OD 表中的发生交通量；$V_j$ 为将来 OD 表中的吸引交通量；$X$ 为将来 OD 表中的生成交通量；$F_{O_i}^m$ 为 $i$ 小区的第 $m$ 次计算发生增长系数；$F_{D_j}^{m+1}$ 为 $j$ 小区的第 $m$ 次计算吸引增长系数；$ϵ$ 为任意给定的误差常数。

若满足误差精度要求，即得到最终结果；否则 $m=m+1$ ，继续迭代。

根据函数 $f(F_{O_i}^m,F_{D_j}^m)$ 的种类不同，增长系数法可以分为常增长系数法 (Unique Growth Factor Method) 、平均增长系数法 (Average Growth Factor Method) 、底特律法 (Detroit Method) 、福莱特法 (Fratar Method) 和佛尼斯法 (Furness Method) ，下面分别讲述。

2.2 常增长系数法

常增长系数法假定 $q_{ij}$ 的增长仅与 $i$ 小区的发生量增长率有关，或仅与 $j$ 小区的吸引量增长率有关，或仅与生成量的增长率有关，是一个常量。

该方法只考虑将来的发生量或吸引量或生成量当中某一个量的增长率对增长函数的影响，忽视了其他变量对增长函数的影响。由于产生量与吸引量的不对称性，因此其预测精度不高，不需要迭代计算。

2.3 平均增长系数法

平均增长系数法假设 $i,j$ 小区之间的分布交通量的增长系数是 $i$ 小区出行发生增长系数和 $j$ 小区出行吸引增长系数的平均值，即：$$f=\frac{1}{2}(F_{O_i}^m+F_{D_j}^m)$$ 该方法的优点是公式简明，易于计算；缺点是收敛慢，迭代次数多，计算精度低。

2.4 底特律法

底特律法假设 $i,j$ 小区间分布交通量 $q_{ij}$ 的增长系数与 $i$ 小区出行发生量和 $j$ 小区出行吸引量增长系数之积成正比，与出行生成量的增长系数成反比，即：$$f=F_{O_i}^m\cdot F_{D_j}^m\cdot \frac{T^m}{X}$$

2.5 福莱特法

福莱特法假设 $i,j$ 小区间分布交通量 $q_{ij}$ 的增长系数不仅与 $i$ 小区的发生增长系数和 $j$ 小区的吸引增长系数有关，还与整个规划区域的其他交通小区的增长系数有关，即：$$f=F_{O_i}^m\cdot F_{D_j}^m\cdot \left(\frac{L_i+L_j}{2}\right)$$$$L_i=\frac{O_i^m}{{\sum }_j(q_{ij}^m\cdot F_{D_j}^m)},L_j=\frac{D_j^m}{{\sum }_i(q_{ij}^m\cdot F_{O_i}^m)}$$ 其中 $L_i,L_j$ 分别表示 $i,j$ 小区的位置系数。

2.6 佛尼斯法

佛尼斯法假设 $i,j$ 小区间分布交通量 $q_{ij}$ 的增长系数与 $i$ 小区的发生增长系数和 $j$ 小区的吸引增长系数都有关系。

首先令吸引增长系数为 1，求满足条件的发生增长系数，接着用调整后的矩阵重新求满足条件的吸引增长系数，完成一个循环迭代过程；然后重新计算发生增长系数，再用调整后的矩阵求吸引增长系数，经过多次循环，直到发生和吸引交通量增长系数满足设定的收敛标准为止。

从上述计算过程可以看出，佛尼斯法计算相对简单，收敛速度相对较快，也适合编程获得预测结果。

2.7 增长系数法的特点

1. 优点

（1）结构简单、实用的方法较多，不需要交通小区之间的距离和时间。

（2）可以适用于小时交通量或日交通量的预测，也可以获得各种交通目的的 OD 交通量。

（3）对于变化较小的 OD 表预测非常有效。

（4）预测铁路车站间的 OD 表非常有效。这时，一般仅增加部分 OD 表，然后把增加部分 OD 表加到现状 OD 表上，求出将来 OD 表。

2. 缺点

1）必须有所有小区的 OD 交通量。

2）对象地区发生如下大规模变化时，该方法不适用：

• 将来的交通小区分布有变化，如新开发等
• 交通小区之间的行驶时间发生变化时
• 土地利用发生较大变化时

3）交通小区之间的交通量较小时，有以下问题：

• 若现状交通量为零，那么将来预测值也为零。
• 对于可靠性较低的 OD 交通量，将来的预测误差将被扩大。

4）因为预测结果因方法的不同而异，所以在选择计算方法时，需要先利用过去的 OD 表预测现状的 OD 表，比较预测精度。

5）将来交通量仅用一个增长系数表示，缺乏合理性。

三、重力模型法

重力模型法 (Gravity Model) 是一种最常用的方法，它根据牛顿的万有引力定律，即两物体间的引力与两物体的质量之积成正比，而与它们之间距离的平方成反比类推而成。

重力模型法出行分布预测考虑了两个交通小区的吸引强度和它们之间的阻力，认为两个交通小区的出行吸引与两个交通小区的出行发生量与吸引量成正比，而与交通小区之间的交通阻抗成反比。在用重力模型进行出行分布预测时，可采用以下几种模型：

3.1 无约束重力模型

Casey 在 1955 年提出了如下重力模型，该模型也是最早出现的重力模型：$$q_{ij}=\alpha \frac{P_i{P}_j}{d_{ij}^2}$$ 式中，$P_i,P_j$ 分别表示 $i$ 小区和 $j$ 小区的人口；$d_{ij}$ 表示 $i,j$ 小区之间的距离；$\alpha$ 为系数。

此模型为无约束重力模型，模型本身不满足以下两个交通守恒约束条件中任何一个：$$\sum _j{q}_{ij}=\alpha P_i\sum _j{P}_j{d}_{ij}^{-2}=O_i\text{\hspace{1em}(1)}$$$$\sum _i{q}_{ij}=\alpha P_j\sum _i{P}_i{d}_{ij}^{-2}=D_j\text{\hspace{1em}(2)}$$ 由于该模型简单地模仿了牛顿的万有引力定律，后来对它进行了许多改进，包括用出行总数代替总人口数，将 $d_{ij}$ 的幂扩展为参数 $\gamma$ (其值一般在 0.6~3.5 之间)，更一般地，可以用出行费用函数 $f(c_{ij})$ 来表示（$c_{ij}$ 指小区 $i,j$ 之间的出行费用）。因此，重力模型可表示为：$$q_{ij}=k{O}_i^{\alpha }{D}_j^{\beta }f(c_{ij})$$ 常见的交通阻抗函数有以下几种形式：$$f(c_{ij})=c_{ij}^{\gamma },e^{-c_{ij}},k{c}_{ij}^{\gamma }{e}^{-c_{ij}}$$ 式中，$k,\gamma$ 为参数。可以通过取对数的方法，将模型线性化，利用最小二乘法来标定。

3.2 单约束重力模型

1. 乌尔希斯重力模型

此模型只满足式 (1) ，即出行发生约束重力模型，其表达式为：$$q_{ij}=O_i{D}_{j}f(c_{ij})/\sum _j{D}_{j}f(c_{ij})$$ 式中，$f(c_{ij})$ 为交通阻抗函数，常用形式为 $f(c_{ij})=c_{ij}^{-\gamma }$；$\gamma$ 为待定系数。

2. 美国公路局重力模型（B. P. R. 模型）$$q_{ij}=O_i{D}_{j}f(c_{ij})K_{ij}/\sum _j{D}_{j}f(c_{ij})K_{ij}$$ 式中，$K_{ij}$ 为调整系数，其计算公式为：$$K_{ij}=(1-Y_{ij}){\lambda }_{ij}/(1-Y_{ij}{\lambda }_{ij})$$ 式中，${\lambda }_{ij}$ 为 $i$ 小区到 $j$ 小区的实际分布交通量与计算分布交通量之比；$Y_{ij}$ 为 $i$ 小区到 $j$ 小区的实际分布交通量与 $i$ 小区的出行发生量之比。

此模型与乌尔希斯模型相比，引进了交通调整系数 $K_{ij}$。这两种模型均满足出行产生约束条件，因此都称为单约束重力模型。 用上述两种重力模型进行交通分布预测时，首先是将预测的交通产生量和吸引量以及将来的交通阻抗参数带入模型进行计算。通常计算出的交通吸引量与给定的交通吸引量并不相同，因此需要进一步迭代。

3.3 双约束重力模型

同时满足守恒条件的 $\alpha$ 是不存在的，因此，将重力模型修改为如下形式：$$\begin{gathered} q_{ij}=a_i{O}_i{b}_j{D}_{j}f(c_{ij}) \\ {a}_i=[\sum _j{b}_j{D}_{j}f(c_{ij}){]}^{-1},b_j=[\sum _i{a}_i{O}_{i}f(c_{ij}){]}^{-1} \end{gathered}$$ 此模型为双约束重力模型。

3.4 重力模型的特点

1. 优 点

1）直观上容易理解。

2）能考虑路网的变化和土地利用对人们的出行产生的影响。

3）特定交通小区之间的 OD 交通量为零时，也能预测。

4）能比较敏感地反映交通小区行驶时间变化的情况。

2. 缺 点

1）模型尽管能考虑到路网的变化和土地利用对出行的影响，但缺乏对人的出行行为的分析，跟实际情况存在一定的偏差。

2）一般，人们的出行距离分布在全区域并非定值，而重力模型将其视为定值。

3）交通小区之间的行驶时间因交通方式和时间段的不同而不同，而重力模型使用了同一时间。

4）内部交通的行驶时间难以给出。

5）交通小区之间的距离较小时，有夸大预测的可能性。

6）利用最小二乘法标定的重力模型计算出的分布交通量必须借助其他方法进行收敛计算。

四、介入机会模型

大纲对这个模型没有做要求，书上纯公式推导，就不按照书上来了，网上找了两篇通俗些的解释。

介入机会模型是从个体目的地选择行为角度建立的预测人类移动的模型。引力模型的基本假设是两个地点之间的旅行次数与两地间的吸引力成正比，与两地间的距离成反比；而介入机会模型认为距离和流动性并不直接相关，该模型认为各个目的地被个体选择的概率并不直接与距离相关，而是与目的地机会数正相关，与介于该目的地与起点之间的所有地点的总机会数（即介入机会）负相关。

参考资料网址：
[1] https://mp.weixin.qq.com/s/r9DJmQyyzJuMEDvDWmHcMA
[2] https://mp.weixin.qq.com/s/kDwBG-R3kS6rghqOdAU-DQ

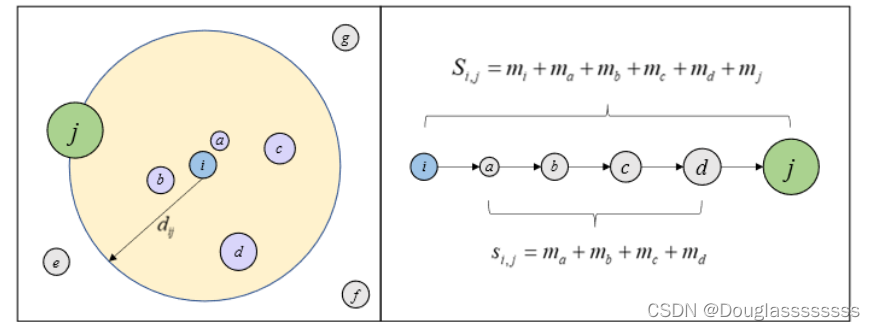
下图${}^{[1]}$给出了介入机会的计算示例。图中的圆心 $i$ 就是人所在的起点，其它地点都是人的潜在目的地，而计算介入机会时，就是以起点 $i$ 为圆心、以到潜在目的地（例如 $j$）的距离为半径画一个圆，里面包含的除了起终点之外的所有地点（a、b、c、d 四个点）的机会数就是介入机会 $s_{ij}$（小写 s）。人当前所在城市的机会就是起点机会 $m_i$，而目的地的机会就是终点机会 $m_j$。（ “机会”通常由人口数量为代表。我们有理由认为，人越多的地方机会也越多。）

在介入机会模型中，每一个从起点出发的个体计算其与所有的潜在目的地之间的距离，并由近到远进行排序。假设个体会以固定的概率被某个地点的机会所吸引并停留在那里，那么位于起点 $i$ 的个体选择地点 $j$ 的概率为：$$P_{ij}=\frac{e^{-\alpha }(s_{i,j}-m_j)-e^{-\alpha s_{i,j}}}{1-e^{-\alpha M}}$$ 式中，$m_j$ 是地点 $j$ 的机会，$s_{i,j}$ 是介入机会，$\alpha$ 是参数，$M$ 是总人口数。

介入机会模型关注机会对目的地选择的影响，强调了人们在移动过程中可能会改变他们的计划，以利用在途中出现的机会。这为解释人口流动行为提供了不同的视角，有助于我们更好地理解人们为什么选择某个目的地以及如何在空间中移动。

介入机会模型与重力模型相比，更加现实地表现了出行者的交通行为。缺点是吸引概率在全区只能取一个定值，缺乏考虑区域的个性特征。

五、最大熵法

最大熵模型 (Entropy Model) 也是随机概率模型之一。典型的最大熵模型有 Wilson 模型和佐佐木 (Sasaki) 模型。

Wilson 模型的特点：

1. 能表现出行者的微观行动；
2. 总交通费用是出行行为选择的结果，对其进行约束脱离现实；
3. 各微观状态的概率相等，即各目的地的选择概率相等的假设没有考虑距离和行驶时间等因素。

佐佐木 (Sasaki) 模型特点：除了事先给定目的地选择概率，其余同上述三个特点。