高斯滤波的理解与学习
高斯滤波的理解与学习微信公众号:幼儿园的学霸目录文章目录高斯滤波的理解与学习目录前言高斯函数一维高斯函数二维高斯函数高斯滤波过程高斯核求解利用高斯核滤波高斯滤波步骤高斯滤波实现高斯滤波标准差与窗口大小的换算实现常规实现分离实现高斯滤波总结高斯函数性质高斯滤波应用参考资料附录高斯函数及频谱绘图代码前言对一幅图像而言,低频部分对应整体灰度级的显示,高频部分对应着图像的细节部分.因此去掉低频部分(或者增
高斯滤波的理解与学习
微信公众号:幼儿园的学霸
目录
文章目录
前言
对一幅图像而言,低频部分对应整体灰度级的显示,高频部分对应着图像的细节部分.因此去掉低频部分(或者增强高频部分)可以锐化图像,去掉高频部分(或者增强低频部分)可以实现模糊/平滑图像的作用.
去除低频或者高频部分可以通过滤波器来完成,但是在时域空间并不能直观看出所谓的高频低频成分,所以就需要做个傅里叶变换,转换成频域,然后直接在频域上把需要去除的频率对应的“基”的权值置零即可.
高斯滤波器是一种线性低通滤波器,能够有效的抑制噪声,平滑图像.其本质是带权值的加权均值滤波,权值大小与滤波器中元素到滤波中心距离有关,卷积核中心权重数值最大,并向四周减小,减小的幅度并不是随意的,而是要求整个卷积核近似高斯函数的图像.高斯滤波器对于抑制服从正态分布的噪声非常有效.
线性滤波器(linear filter) :输出图像上每个像素点的值都是由输入图像各像素点值加权求和的结果.其原始数据与滤波结果是一种算术运算,即用加减乘除等运算实现,如方框滤波(BoxFilter)、均值滤波(MeanBlur)、高斯滤波(GaussianBlur)等.由于线性滤波器是算术运算,有固定的模板,因此滤波器的转移函数是可以确定并且是唯一的.
非线性滤波器(non-linear filter):非线性滤波的算子中包含了取绝对值、置零等非线性运算.其原始数据与滤波结果是一种逻辑关系,即用逻辑运算实现,如最大值滤波器、最小值滤波器、中值滤波(medianBlur)和双边滤波(bilateralFilter)等,是通过比较一定邻域内的灰度值大小来实现的,没有固定的模板,因而也就没有特定的转移函数(因为没有模板作傅里叶变换),另外,膨胀和腐蚀也是通过最大值、最小值滤波器实现的.
思考1:为什么要进行 加权均值 ?一幅图像中轮廓和边缘这种变化比较剧烈的地方高频信号(噪声和噪声周边的像素相比,其灰度变化同样比较剧烈),其他的部分(可反应整副图像的强度)是低频信号,所以经过低通滤波器后图像的轮廓和边缘信号会被滤掉一部分,直观感受是图片变模糊了,这是平滑.从另一方面讲,加权是将一个像素用邻域几个像素的均值代替,这样会使信号的变化变得平缓(拉大小的值,拉小大的值),信号变化剧烈的地方是高频信号,所以,这样就达到了低通的效果,而低通可以滤除高频噪声.因此加权的目的在于实现低通.
思考2:如何实现 加权均值 中的求平均目的? 滤波核前面的系数等于矩阵中所有元素之和的倒数
高斯函数
计算高斯滤波的滤波核之前先了解一下高斯函数.
高斯函数在图像处理中出现的频率相当高.
一维高斯函数
f
(
x
)
=
1
2
π
σ
e
−
(
x
−
μ
)
2
2
σ
2
f(x)=\frac{1}{\sqrt{2 \pi} \sigma } e^{\frac{-(x-\mu)^{2} }{2 \sigma ^ 2}}
f(x)=2πσ1e2σ2−(x−μ)2
其中,μ是x的均值,σ是x的方差.本质上,x,μ都是空间中的坐标,x是卷积核内任一点的坐标,μ是卷积核中心的坐标.
由于每次计算时,都是以当前计算点为原点(中心点就是原点),因此均值μ等于0.所以公式进一步简化为:
f
(
x
)
=
1
2
π
σ
e
−
x
2
2
σ
2
f(x)=\frac{1}{\sqrt{2 \pi} \sigma } e^{\frac{-x^{2} }{2 \sigma ^ 2}}
f(x)=2πσ1e2σ2−x2
其函数曲线如下图所示:

可以看到其是一钟形曲线,σ决定了分布的形状或者说表征了钟的宽度,σ越小形状越瘦高,σ越大越矮胖
二维高斯函数
在计算机视觉中,图像是二维的,因此引入下面的二维高斯函数.
二维高斯函数为X,Y两个方向的一维高斯函数的乘积:
f
(
x
,
y
)
=
f
(
x
)
f
(
y
)
=
1
2
π
σ
x
e
−
(
x
−
μ
x
)
2
2
σ
x
2
1
2
π
σ
y
e
−
(
x
−
μ
y
)
2
2
σ
y
2
f(x, y)=f(x) f(y)=\frac{1}{\sqrt{2 \pi} \sigma_{x}} e^{-\frac{\left(x-\mu_{x}\right)^{2}}{2 \sigma_{x}^{2}}} \frac{1}{\sqrt{2 \pi} \sigma_{y}} e^{-\frac{\left(x-\mu_{y}\right)^{2}}{2 \sigma_{y}^{2}}}
f(x,y)=f(x)f(y)=2πσx1e−2σx2(x−μx)22πσy1e−2σy2(x−μy)2
同样,在图像滤波中,一般情况下
μ
x
=
μ
y
=
0
\mu_x=\mu_y=0
μx=μy=0,因此二维高斯函数可表示如下:
f
(
x
,
y
)
=
f
(
x
)
f
(
y
)
=
1
2
π
σ
2
e
−
x
2
+
y
2
2
σ
2
f(x, y)=f(x) f(y)=\frac{1}{2 \pi \sigma^{2}} e^{-\frac{x^{2}+y^{2}}{2 \sigma^{2}}}
f(x,y)=f(x)f(y)=2πσ21e−2σ2x2+y2
其中,(x,y)为点的坐标,在图像处理中,其为整数.
其函数曲线如下图所示:

从函数曲线可以看到,在整个定义域内,高斯函数值都是非负的,
f
(
x
,
y
)
>
0
f(x, y)>0
f(x,y)>0成立,这也决定了高斯核中所有元素的值均为正值.
高斯滤波过程
高斯核求解
要想得到一个高斯核,可以对高斯函数进行离散化,得到的高斯函数值作为高斯核的元素.例如:要产生一个3x3的高斯核,以高斯核的中心位置为坐标原点进行离散取样, 那么高斯核中心的8邻域坐标为:

将各个位置的坐标代入到高斯函数中,得到的值就是初步的高斯核:

假设σ=1,则上面的高斯核求解结果如下:

上面初步计算3x3高斯核的权重和为0.7794836.考虑这样一个问题,假若某一邻域内所有像素的灰度值为255,那么通过该高斯核进行卷积之后,模板中心像素的灰度值为0.7794836×255=198.77 < 255,偏离了实际的灰度值,使得图像亮度相比原图偏暗,产生了误差.因此有必要对该高斯核进行归一化处理,保证权重和为1以保证图像的均匀灰度区域不受影响.
归一化的原因更加正确的表述应该为:对灰度级为常数的图像区域,高斯模板的响应该为1.这样才能确保灰度级为常数的图像区域经过高斯模板处理之后,依旧为其本身,而不是被改变为其他灰度级.
将求得的高斯核中各权重值除以权重和进行归一化后如下:

作为对比,在matlab中,
z = fspecial('gaussian', [3 3], 1);得到的结果和上面结果一致.
上面归一化后求解的高斯核为小数形式的.
除了小数形式,高斯核也可以写为整数形式.只用对求得的初始高斯核进行取整处理,就能得到整数形式的高斯核.从高斯函数图像可以看到:1)从曲线中心位置到两端,高斯函数值是单调递减的;2)曲线位于x轴上方,其值总是正的.因此高斯核中距离中心最远的位置(如高斯核左上角)的元素总是最小的,如果进行取整,那么左上角元素的最小值也要保证≥1.所以对求解整数形式的高斯核过程如下:
1). 高斯核左上角的值归一化为1.即高斯核中所有元素均除以左上角的元素.在本例中,左上角的元素为0.058549833,归一化后高斯核为:

2).取整(对于取整方式,未查找到具体的原则.有文章选择了选择向下取整的方式,也许有向上取整,或者四舍五入等方式,但是从不同取整方式的结果来看,四舍五入的取整方式更接近于小数形式的结果).
3).取整后,高斯核所有元素的和明显大于1,为了保证图像的均匀灰度区域不受影响,因此需要进行权重归一化,给高斯核一系数,以保证高斯和所有元素的和与系数的乘积为1.显然,该系数为高斯核和的倒数,该例中取整、归一化后高斯核为:

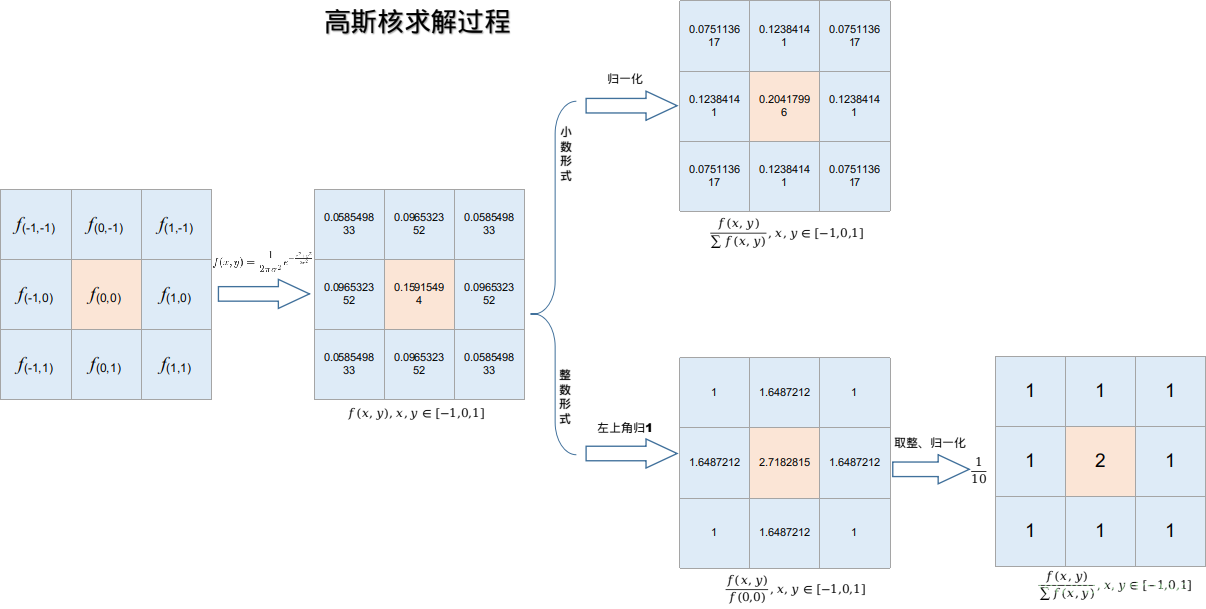
总结高斯核求解过程图示如下:

利用高斯核滤波
滤波计算过程和CNN中的单通道卷积过程一致,只是此处滤波时的步长为1,滤波核为单通道,而CNN中卷积步长可以指定为1,2等值.
有了高斯核,就可以对图像进行高斯滤波了.具体滤波过程和其他滤波方法一致.以一个3x3数据为例,利用上面求解的高斯核进行滤波.
其中心点的高斯滤波过程如下:

图中中心像素值为50,经过滤波后其值仍为50,这只是由于数字选择的原因导致其凑巧在数值上相等而已.如果将中心像素值修改为52,其滤波后值也为50.
在边界附近的点,其邻域内没有足够的点进行滤波处理,因此在滤波之前需要进行上下、左右边界扩充操作,各边界扩充的宽度为滤波半径大小.具体的边界扩充类型可以参考OpenCV中BorderTypes指定的类型进行.
考虑此,对上述3x3输入进行滤波的过程如下:

易计算得滤波前输入像素的和为450,滤波后输出矩阵各元素相加后的和仍为450,即图像的亮度在经过该高斯核滤波前后没有发生变化.
高斯滤波步骤
按照上面的流程,可以归纳高斯滤波的步骤如下:
1.生成高斯核.根据选择的滤波半径以及标准差,确定高斯核邻域内各点到中心点的距离,代入二维高斯函数,求解高斯核各位置值,然后进行归一化等处理;
2.边界扩充.根据高斯核大小对输入图像进行扩充边界操作;
3.卷积.针对图像矩阵中的某个元素P,把高斯核的中心和待处理元素P空间对齐,将高斯核中各权值和P的邻域内元素相乘后相加,作为P的输出值;
4.对图像中的每个元素(不包含边界扩充的元素)进行步骤3的操作,得到的结果就是高斯滤波的结果.
从上面的步骤可以看到,高斯滤波仅考虑了图像中各元素空间位置之间的关系,没有将像素值之间的关系考虑进去. 而之前讲到的双边滤波就不仅考虑像素空间之间的关系,同时考虑像素值之间的关系,它是空间域和像素值域之间的综合结果.并且空间域和像素值域的求解都是套用高斯函数公式得到的.只是f(x,y)中x,y,μ的含义不同:针对空间域,它和这里的高斯核是一样的,x,y,μ表示的是空间位置,而μ=0;针对值域,x,y表示每一点的像素值,μ表示中心的像素值.所以它不光考虑了像素在空间中位置远近程度的影响,还考虑了像素亮度相近程度的影响.从这个角度来看,双边滤波就很好理解了.
高斯滤波实现
根据上面的滤波步骤,可以比较方便的实现高斯滤波代码.
高斯滤波标准差与窗口大小的换算
如下图所示为高斯函数的分布特点.一般3σ外的数值已接近于0,可忽略.数值分布在(μ—3σ,μ+3σ)中的概率为0.997,或者说以均值为中心,半径为3σ的范围内已经包含了高斯函数99.7%以上的信息。如果高斯核的尺寸大,那么相应的标准差σ也更大;相对应,如果σ大,那么意味着高斯核的尺寸也要相应的进行增加.因此当我们知道高斯核的大小后,可以推断出标准差的值.

我们大概可以感受到高斯核的半径大约为3σ的大小.据此,在OpenCV中,有下面公式:
σ
=
0.3
∗
(
k
s
i
z
e
2
−
1
)
+
0.8
\sigma = 0.3*(\frac{ksize}{2}-1)+0.8
σ=0.3∗(2ksize−1)+0.8
推导标准差的取值.公式中0.3比较好理解,但0.8的来历并不是很清楚.
当知道标准差而不知道高斯核尺寸时,同样可以由上式进行反向求解,得到高斯核尺寸,公式如下:
k
s
i
z
e
=
[
2
∗
(
3
σ
)
+
1
]
∣
1
ksize = [2*(3\sigma) + 1 ] | 1
ksize=[2∗(3σ)+1]∣1
公式为先取整,然后和1进行按位或运算,以保证高斯核尺寸为奇数.
OpenCV中该部分代码如下:

代码中半径为σ的3或4倍.
4倍的来源不明,无资料说明
实现
常规实现
常规实现过程按照上面的公式计算即可.其中高斯核或标准差的计算按上节公式实现.
代码如下:
#include <iostream>
#include <chrono>
#include <opencv2/opencv.hpp>
#include <numeric>
/*!
* 生成小数形式的二维高斯核
* @param ksize 高斯核大小,奇数.当ksize<=0,并且sigma>0时,自动根据sigma计算ksize
* @param sigma 高斯滤波标准差.当sigma<=0,并且ksize>0为奇数时,自动根据ksize计算sigma
* @return 小数形式的高斯核.CV_32FC1.尺寸:ksize * ksize
* @author liheng
*/
cv::Mat GetGaussianKernel( int ksize, float sigma)
{
//根据sigma自动计算ksize
if( ksize <= 0 && sigma > 0 )
ksize = cvRound((sigma*3)*2 + 1)|1;// | 1操作以保证ksize为奇数
//校验ksize
CV_Assert( ksize > 0 && ksize % 2 == 1);
//未设定sigma值时,根据窗口大小进行计算
sigma = (sigma>0 ? sigma : 0.3f*((ksize-1)*0.5f - 1) + 0.8f);
auto sigma2_inverse = 1.0/(2*sigma*sigma);// 1/(2*sigma^2)
cv::Mat kernel(ksize, ksize,CV_32FC1);
const int center = ksize/2;//高斯核中心坐标
for(int row=0;row<ksize;++row)
{
int y=row-center; //以center为中心,第row行的 y坐标
auto y2 = y*y;//y^2
for(int col=0;col<ksize;++col)
{
int x=col-center; //以center为中心,第col列的x坐标
//float f_xy = 1.0/(2*CV_PI*sigma*sigma) * std::exp( -(x*x+y*y)/(2*sigma*sigma) );
float f_xy = std::exp(-(x*x+y2)*sigma2_inverse );//减少不必要计算;系数在后面归一化时会被消去;
kernel.at<float>(row,col) = f_xy;
}
}
//小数形式高斯核
auto sum = cv::sum(kernel)[0];
kernel /= sum;
整数形式高斯核
左上角系数归一化为1
//kernel /= kernel.at<float>(0,0);
向下取整
//kernel.convertTo(kernel,CV_32SC1);//向上取整?
//kernel.convertTo(kernel,CV_32FC1);//系数未计算
return kernel;
}
/*!
* 利用卷积核对输入图像进行二维卷积(滤波)
* @param src 输入.CV_8UC1
* @param dst 输出.CV_8UC1
* @param kernel 卷积核(相关核).CV_32FC1. kernel.size()需要为奇数
* @note 该函数在OpenCV中的对应函数:cv::filter2D(...)
* @author liheng
*/
void Filter2D(const cv::Mat& src,cv::Mat& dst,const cv::Mat& kernel)
{
CV_Assert( kernel.cols % 2 == 1 && kernel.rows % 2 == 1);
//边界填充
int border_lr = kernel.cols/2;//左右填充宽度
int border_tb = kernel.rows/2;//上下填充宽度
cv::Mat borderedSrc;
cv::copyMakeBorder(src,borderedSrc,border_tb,border_tb,border_lr,border_lr,cv::BORDER_REFLECT);
dst.create(src.size(),src.type());
//对图像中各元素(不包含填充元素)分别进行滤波
int rows = borderedSrc.rows;
int cols = borderedSrc.cols;
for(int row=border_tb; row<rows-border_tb; ++row)
{
for(int col=border_lr; col<cols-border_lr; ++col)
{
//遍历卷积核邻域求加权和作为该点输出值
float sum = 0;
for(int y=-border_tb; y<=border_tb; ++y)//邻域高度:2*border_tb+1
{
for(int x=-border_lr;x<=border_lr; ++x)//邻域宽度:2*border_lr+1
sum += kernel.at<float>(y+border_tb,x+border_lr)*borderedSrc.at<uchar>(row+y,col+x);//权重与元素相乘
}
//输出
dst.at<uchar>(row-border_tb,col-border_lr) = cv::saturate_cast<uchar>(sum);
}
}
}
/*!
* 自定义实现高斯滤波.原始版本,未采用分离卷积进行加速
* @param src 输入.CV_8UC1
* @param dst 输出.CV_8UC1
* @param ksize 高斯核大小,奇数.当ksize<=0,并且sigma>0时,自动根据sigma计算ksize
* @param sigma 高斯滤波标准差.当sigma<=0,并且ksize>0为奇数时,自动根据ksize计算sigma
* @author liheng
*/
void MyGaussianFilter(const cv::Mat& src,cv::Mat& dst,int ksize,float sigma)
{
//生成二维高斯核
cv::Mat kernel = GetGaussianKernel(ksize,sigma);
//滤波
Filter2D(src,dst,kernel);
}
int main(int argc, char *argv[])
{
cv::Mat kernel = GetGaussianKernel(3,1);
std::cout<<"二维高斯核:"<<std::endl;
std::cout<<kernel<<std::endl;
cv::Mat data = (cv::Mat_<uchar>(3,3)<<
10,20,30,
40,50,60,
70,80,90);
//
cv::Mat dst;
MyGaussianFilter(data,dst,3,1);
std::cout<<"自定义实现结果::"<<std::endl;
std::cout<<dst<<std::endl;
cv::Mat dst2;
cv::filter2D(data,dst2,CV_8UC1,kernel,cv::Point(-1,-1),0,cv::BORDER_REFLECT);
std::cout<<"filter2D结果::"<<std::endl;
std::cout<<dst2<<std::endl;
cv::GaussianBlur(data,data,cv::Size(3,3),1,1,cv::BORDER_REFLECT);
std::cout<<"cv::GaussianBlur结果::"<<std::endl;
std::cout<<data<<std::endl;
//输出结果如下:
/**
二维高斯核:
[0.075113609, 0.1238414, 0.075113609;
0.1238414, 0.20417996, 0.1238414;
0.075113609, 0.1238414, 0.075113609]
自定义实现结果::
[ 21, 28, 35;
43, 50, 57;
65, 72, 79]
filter2D结果::
[ 21, 28, 35;
43, 50, 57;
65, 72, 79]
cv::GaussianBlur结果::
[ 21, 28, 35;
43, 50, 57;
65, 72, 79]
**/
return 0;
}
可以参考上面图片中流程以辅助理解.
上面的滤波过程,其循环次数为row*col*(ksize*ksize),其中row,col为图像的尺寸.其时间复杂度为
O
(
N
2
)
O(N^2)
O(N2),随着高斯核尺寸的增加而呈平方增长,当高斯核尺寸较大时,其运算效率比较低.为了提高运算速度,可以将二维的高斯核进行拆分,然后分别进行滤波.
分离实现高斯滤波
从二维高斯函数的公式可以看到,其为两个一维高斯函数的乘积.因此二维高斯核具有可分离性,可以将高斯核分为两个一维高斯核的乘积,如下图所示:

同样,利用高斯函数进行卷积(高斯滤波)的过程也具有可分离性. 其示意图如下:

证明过程如下.
高斯滤波函数如上面所示的
f
(
x
,
y
)
f(x,y)
f(x,y),输入图像为
I
(
x
,
y
)
I(x,y)
I(x,y),两者进行卷积运算,记边界索引为
a
=
n
−
1
2
a=\frac{n-1}{2}
a=2n−1,则两者卷积过程表示如下:
两者之间为 离散二维卷积.下面公式即为离散二维卷积的定义.
f
(
x
,
y
)
∗
I
(
x
,
y
)
=
∑
i
=
−
a
a
∑
j
=
−
a
a
f
(
i
,
j
)
I
(
x
−
i
,
y
−
j
)
=
∑
i
=
−
a
a
∑
j
=
−
a
a
I
(
x
−
i
,
y
−
j
)
1
2
π
σ
2
e
−
i
2
+
j
2
2
σ
2
=
∑
i
=
−
a
a
[
1
2
π
σ
e
−
i
2
2
σ
2
∗
[
∑
j
=
−
a
a
I
(
x
−
i
,
y
−
j
)
∗
1
2
π
σ
e
−
j
2
2
σ
2
]
]
(1)
\begin{aligned} f(x,y)*I(x,y) &= \sum_{i=-a}^{a} \sum_{j=-a}^{a}f(i,j)I(x-i,y-j) \\ &= \sum_{i=-a}^{a} \sum_{j=-a}^{a} I(x-i,y-j) \frac{1}{2 \pi \sigma^{2}} e^{-\frac{i^{2}+j^{2}}{2 \sigma^{2}}} \\ &= \sum_{i=-a}^{a} \left[ \frac{1}{\sqrt{2 \pi} \sigma } e^{\frac{-i^{2} }{2 \sigma ^ 2}} * \left[ \sum_{j=-a}^{a} I(x-i,y-j)*\frac{1}{\sqrt{2 \pi} \sigma } e^{\frac{-j^{2} }{2 \sigma ^ 2}} \right] \right] \\ \end{aligned} \tag{1}
f(x,y)∗I(x,y)=i=−a∑aj=−a∑af(i,j)I(x−i,y−j)=i=−a∑aj=−a∑aI(x−i,y−j)2πσ21e−2σ2i2+j2=i=−a∑a[2πσ1e2σ2−i2∗[j=−a∑aI(x−i,y−j)∗2πσ1e2σ2−j2]](1)
记
f
(
y
)
=
1
2
π
σ
e
−
y
2
2
σ
2
f(y)=\frac{1}{\sqrt{2 \pi} \sigma } e^{\frac{-y^{2} }{2 \sigma ^ 2}}
f(y)=2πσ1e2σ2−y2,则上面第2个中括号部分整理如下:
∑
j
=
−
a
a
I
(
x
−
i
,
y
−
j
)
∗
1
2
π
σ
e
−
j
2
2
σ
2
=
f
(
y
)
∗
I
(
x
−
i
,
y
)
(2)
\begin{aligned} \sum_{j=-a}^{a} I(x-i,y-j)*\frac{1}{\sqrt{2 \pi} \sigma } e^{\frac{-j^{2} }{2 \sigma ^ 2}} = f(y)*I(x-i,y) \end{aligned} \tag{2}
j=−a∑aI(x−i,y−j)∗2πσ1e2σ2−j2=f(y)∗I(x−i,y)(2)
可视为图像I与f(y)之间的卷积运算.
记
f
(
x
)
=
1
2
π
σ
e
−
x
2
2
σ
2
f(x)=\frac{1}{\sqrt{2 \pi} \sigma } e^{\frac{-x^{2} }{2 \sigma ^ 2}}
f(x)=2πσ1e2σ2−x2,同时将公式(2)代入公式(1)整理:
f
(
x
,
y
)
∗
I
(
x
,
y
)
=
∑
i
=
−
a
a
[
1
2
π
σ
e
−
i
2
2
σ
2
∗
[
f
(
y
)
∗
I
(
x
−
i
,
y
)
]
]
=
f
(
x
)
∗
(
f
(
y
)
∗
I
(
x
,
y
)
)
(3)
\begin{aligned} f(x,y)*I(x,y) &= \sum_{i=-a}^{a} \left[ \frac{1}{\sqrt{2 \pi} \sigma } e^{\frac{-i^{2} }{2 \sigma ^ 2}} * \left[ f(y)*I(x-i,y) \right] \right] \\ &= f(x)*\left( f(y)*I(x,y) \right) \\ \end{aligned} \tag{3}
f(x,y)∗I(x,y)=i=−a∑a[2πσ1e2σ2−i2∗[f(y)∗I(x−i,y)]]=f(x)∗(f(y)∗I(x,y))(3)
在上面推导过程中,f(y),f(x)并不代表具体的行列顺序,f(x)可以表示行方向,也可以代表列方向,f(y)同理.因此公式(3)可整理为:
f
(
x
,
y
)
∗
I
(
x
,
y
)
=
f
(
x
)
∗
(
f
(
y
)
∗
I
(
x
,
y
)
)
=
I
(
x
,
y
)
∗
f
(
y
)
∗
f
(
x
)
=
I
(
x
,
y
)
∗
f
(
x
)
∗
f
(
y
)
(4)
\begin{aligned} f(x,y)*I(x,y) &= f(x)*\left( f(y)*I(x,y) \right) \\ &= I(x,y)*f(y)*f(x) \\ &= I(x,y)*f(x)*f(y) \end{aligned} \tag{4}
f(x,y)∗I(x,y)=f(x)∗(f(y)∗I(x,y))=I(x,y)∗f(y)∗f(x)=I(x,y)∗f(x)∗f(y)(4)
从而:高斯函数进行卷积(高斯滤波)的过程同样具有可分离性得证.
上面结论可以进行推广.如果卷积核kernel是可分离的,并且
k
e
r
n
e
l
=
k
e
r
n
e
l
1
∗
k
e
r
n
e
l
2
kernel=kernel1*kernel2
kernel=kernel1∗kernel2,则对图像I进行卷积有:
I
∗
k
e
r
n
e
l
=
I
∗
(
k
e
r
n
e
l
1
∗
k
e
r
n
e
l
2
)
=
(
I
∗
k
e
r
n
e
l
1
)
∗
k
e
r
n
e
l
2
\begin{aligned} I*kernel &= I*(kernel1*kernel2) \\ &= (I*kernel1)*kernel2 \end{aligned}
I∗kernel=I∗(kernel1∗kernel2)=(I∗kernel1)∗kernel2
需要注意的是,上面的卷积核kernel为一维水平方向和一维垂直方向共2个卷积核的全卷积,这2个卷积核是满足交换律的,但是对于多个卷积核的全卷积,其并不满足交换律.
对于均值滤波,其卷积核也是可分离的,如下:
1
9
[
1
1
1
1
1
1
1
1
1
]
=
1
3
[
1
1
1
]
∗
1
3
[
1
1
1
]
\frac{1}{9}\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right]=\frac{1}{3}\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right] * \frac{1}{3}\left[\begin{array}{lll} 1 & 1 & 1 \end{array}\right]
91⎣⎡111111111⎦⎤=31⎣⎡111⎦⎤∗31[111]
用于边缘检测的Sobel卷积核也是可分离的,如下:
[
−
1
0
1
−
2
0
2
−
1
0
1
]
=
[
1
2
1
]
×
[
−
1
0
1
]
\left[\begin{array}{lll} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right]=\left[\begin{array}{l} 1 \\ 2 \\ 1 \end{array}\right] \times\left[\begin{array}{lll} -1 & 0 & 1 \end{array}\right]
⎣⎡−1−2−1000121⎦⎤=⎣⎡121⎦⎤×[−101]
CNN中非对称卷积
(Asymmetric Convolution)/空间可分离卷积(Spatial Separable Convolution)的思想和这里有点相似.
按照公式的推导结论,可对原始高斯滤波进行优化,改写为可分离卷积的形式.
为方便,上一小节代码同样拷贝到该代码中.
#include <iostream>
#include <chrono>
#include <opencv2/opencv.hpp>
#include <numeric>
/*!
* 生成小数形式的二维高斯核
* @param ksize 高斯核大小,奇数.当ksize<=0,并且sigma>0时,自动根据sigma计算ksize
* @param sigma 高斯滤波标准差.当sigma<=0,并且ksize>0为奇数时,自动根据ksize计算sigma
* @return 小数形式的高斯核.CV_32FC1.尺寸:ksize * ksize
* @author liheng
*/
cv::Mat GetGaussianKernel( int ksize, float sigma)
{
//根据sigma自动计算ksize
if( ksize <= 0 && sigma > 0 )
ksize = cvRound((sigma*3)*2 + 1)|1;// | 1操作以保证ksize为奇数
//校验ksize
CV_Assert( ksize > 0 && ksize % 2 == 1);
//未设定sigma值时,根据窗口大小进行计算
sigma = (sigma>0 ? sigma : 0.3f*((ksize-1)*0.5f - 1) + 0.8f);
auto sigma2_inverse = 1.0/(2*sigma*sigma);// 1/(2*sigma^2)
cv::Mat kernel(ksize, ksize,CV_32FC1);
const int center = ksize/2;//高斯核中心坐标
for(int row=0;row<ksize;++row)
{
int y=row-center; //以center为中心,第row行的 y坐标
auto y2 = y*y;//y^2
for(int col=0;col<ksize;++col)
{
int x=col-center; //以center为中心,第col列的x坐标
//float f_xy = 1.0/(2*CV_PI*sigma*sigma) * std::exp( -(x*x+y*y)/(2*sigma*sigma) );
float f_xy = std::exp(-(x*x+y2)*sigma2_inverse );//减少不必要计算;系数在后面归一化时会被消去;
kernel.at<float>(row,col) = f_xy;
}
}
//小数形式高斯核
auto sum = cv::sum(kernel)[0];
kernel /= sum;
整数形式高斯核
左上角系数归一化为1
//kernel /= kernel.at<float>(0,0);
向下取整
//kernel.convertTo(kernel,CV_32SC1);//向上取整?
//kernel.convertTo(kernel,CV_32FC1);//系数未计算
return kernel;
}
/*!
* 利用卷积核对输入图像进行卷积(滤波)
* @param src 输入.CV_8UC1
* @param dst 输出.CV_8UC1
* @param kernel 卷积核(相关核).CV_32FC1. kernel.size()需要为奇数
* @note 该函数在OpenCV中的对应函数:cv::filter2D(...)
* @author liheng
*/
void Filter2D(const cv::Mat& src,cv::Mat& dst,const cv::Mat& kernel)
{
CV_Assert( kernel.cols % 2 == 1 && kernel.rows % 2 == 1);
//边界填充
int border_lr = kernel.cols/2;//左右填充宽度
int border_tb = kernel.rows/2;//上下填充宽度
cv::Mat borderedSrc;
cv::copyMakeBorder(src,borderedSrc,border_tb,border_tb,border_lr,border_lr,cv::BORDER_REFLECT);
dst.create(src.size(),src.type());
//对图像中各元素(不包含填充元素)分别进行滤波
int rows = borderedSrc.rows;
int cols = borderedSrc.cols;
for(int row=border_tb; row<rows-border_tb; ++row)
{
for(int col=border_lr; col<cols-border_lr; ++col)
{
//遍历卷积核邻域求加权和作为该点输出值
float sum = 0;
for(int y=-border_tb; y<=border_tb; ++y)//邻域高度:2*border_tb+1
{
for(int x=-border_lr;x<=border_lr; ++x)//邻域宽度:2*border_lr+1
sum += kernel.at<float>(y+border_tb,x+border_lr)*borderedSrc.at<uchar>(row+y,col+x);//权重与元素相乘
}
//输出
dst.at<uchar>(row-border_tb,col-border_lr) = cv::saturate_cast<uchar>(sum);
}
}
}
/*!
* 自定义实现高斯滤波.原始版本,未采用分离卷积进行加速
* @param src 输入.CV_8UC1
* @param dst 输出.CV_8UC1
* @param ksize 高斯核大小,奇数.当ksize<=0,并且sigma>0时,自动根据sigma计算ksize
* @param sigma 高斯滤波标准差.当sigma<=0,并且ksize>0为奇数时,自动根据ksize计算sigma
* @author liheng
*/
void MyGaussianFilter(const cv::Mat& src,cv::Mat& dst,int ksize,float sigma)
{
//生成二维高斯核
cv::Mat kernel = GetGaussianKernel(ksize,sigma);
//滤波
Filter2D(src,dst,kernel);
}
//
/*!
* 生成小数形式的 "一维" 高斯核
* @param ksize 高斯核大小,奇数.当ksize<=0,并且sigma>0时,自动根据sigma计算ksize
* @param sigma 高斯滤波标准差.当sigma<=0,并且ksize>0为奇数时,自动根据ksize计算sigma
* @return 小数形式的高斯核.CV_32FC1.尺寸: 1 * ksize
* @author liheng
*/
cv::Mat GetSingleDimGaussianKernel( int ksize, double sigma)
{
//根据sigma自动计算ksize
if( ksize <= 0 && sigma > 0 )
ksize = cvRound((sigma*3)*2 + 1)|1;// | 1操作以保证ksize为奇数
//校验ksize
CV_Assert( ksize > 0 && ksize % 2 == 1);
//未设定sigma值时,根据窗口大小进行计算
sigma = (sigma>0 ? sigma : 0.3f*((ksize-1)*0.5f - 1) + 0.8f);
auto sigma2_inverse = 1.0/(2*sigma*sigma);// 1/(2*sigma^2)
cv::Mat kernel(1, ksize,CV_32FC1);
const int center = ksize/2;//高斯核中心坐标
for(int col=0;col<ksize;++col)
{
int x=col-center; //以center为中心,第col列的 x坐标
//float f_x = 1.0/(std::sqrt(2*CV_PI)*sigma) * std::exp( -(x*x)/(2*sigma*sigma) );
float f_x = std::exp( -(x*x)*sigma2_inverse );//减少不必要计算;系数在后面归一化时会被消去;
kernel.at<float>(0,col) = f_x;
}
auto sum = cv::sum(kernel)[0];
kernel /= sum;
return kernel;
}
/*!
* 自定义实现高斯滤波.改进版.利用高斯函数的可分离性以加速卷积过程
* @param src 输入.CV_8UC1
* @param dst 输出.CV_8UC1
* @param ksize 高斯核大小,奇数.当ksize<=0,并且sigma>0时,自动根据sigma计算ksize
* @param sigma 高斯滤波标准差.当sigma<=0,并且ksize>0为奇数时,自动根据ksize计算sigma
* @author liheng
*/
void separateGaussianFilter(const cv::Mat& src,cv::Mat& dst,int ksize,float sigma)
{
//获取水平和竖直高斯核
cv::Mat kernelX = GetSingleDimGaussianKernel(ksize,sigma);
cv::Mat kernelY = kernelX.t();
cv::Mat Z;//中间变量.存储水平方向高斯滤波后结果.
//水平方向高斯滤波
Filter2D(src,Z,kernelX);
//对水平方向滤波后结果进行竖直方向高斯滤波
Filter2D(Z,dst,kernelY);
}
int main(int argc, char *argv[])
{
cv::Mat kernel = GetGaussianKernel(3,1);
std::cout<<"二维高斯核:"<<std::endl;
std::cout<<kernel<<std::endl;
cv::Mat data = (cv::Mat_<uchar>(3,3)<<
10,20,30,
40,50,60,
70,80,90);
//
cv::Mat dst;
MyGaussianFilter(data,dst,3,1);
std::cout<<"自定义实现结果::"<<std::endl;
std::cout<<dst<<std::endl;
cv::Mat dst1;
separateGaussianFilter(data,dst1,3,1);
std::cout<<"自定义分离实现结果::"<<std::endl;
std::cout<<dst1<<std::endl;
cv::Mat dst2;
cv::filter2D(data,dst2,CV_8UC1,kernel,cv::Point(-1,-1),0,cv::BORDER_REFLECT);
std::cout<<"filter2D结果::"<<std::endl;
std::cout<<dst2<<std::endl;
cv::GaussianBlur(data,data,cv::Size(3,3),1,1,cv::BORDER_REFLECT);
std::cout<<"cv::GaussianBlur结果::"<<std::endl;
std::cout<<data<<std::endl;
//输出结果如下:
/**
二维高斯核:
[0.075113609, 0.1238414, 0.075113609;
0.1238414, 0.20417996, 0.1238414;
0.075113609, 0.1238414, 0.075113609]
自定义实现结果::
[ 21, 28, 35;
43, 50, 57;
65, 72, 79]
自定义分离实现结果::
[ 21, 28, 35;
43, 50, 57;
65, 72, 79]
filter2D结果::
[ 21, 28, 35;
43, 50, 57;
65, 72, 79]
cv::GaussianBlur结果::
[ 21, 28, 35;
43, 50, 57;
65, 72, 79]
**/
return 0;
}
从代码可以看到,其实现原理还是比较简单的.首先得到一维的高斯核,在卷积(滤波)的过程中,保持行不变,列变化,在水平方向上做卷积运算;接着在上述得到的结果上,保持列不边,行变化,在竖直方向上做卷积运算. 这样分解开来,算法的时间复杂度为
O
(
N
)
O(N)
O(N),运算量和高斯核的尺寸呈线性增长.
利用该分离性,卷积复杂度大大降低,并且我们也不需要生成二维卷积核,而只要生成一维核即可,这也减少了计算量.在实际应用中,甚至还可以直接存储常用维数的高斯核数值来提升性能.在OpenCV的源码中就存储了ksize=1,3,5,7这4中高斯核的权值,当ksize<=7时直接取存储的值而不必单独计算一遍高斯核.
总结
高斯函数性质
高斯函数具有五个重要的性质,这些性质使得它在早期图像处理中特别有用.这些性质表明,高斯平滑滤波器无论在空间域还是在频率域都是十分有效的低通滤波器,且在实际图像处理中得到了工程人员的有效使用.高斯函数具有五个十分重要的性质,它们是:
1).二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的.一般来说,一幅图像的边缘方向是事先不知道的,因此,在滤波前是无法确定一个方向上比另一方向上需要更多的平滑.旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向.
2).高斯函数是单值函数.这表明,高斯滤波器用像素邻域的加权均值来代替该点的像素值,而每一邻域像素点权值是随该点与中心点的距离单调增减的.这一性质是很重要的,因为边缘是一种图像局部特征,如果平滑运算对离算子中心很远的像素点仍然有很大作用,则平滑运算会使图像失真.
3).高斯函数的傅立叶变换频谱是单瓣的.如下图所示,这一性质是高斯函数傅立叶变换等于高斯函数本身这一事实的直接推论.图像常被不希望的高频信号所污染(噪声和细纹理).而所希望的图像特征(如边缘),既含有低频分量,又含有高频分量.高斯函数傅立叶变换的单瓣意味着平滑图像不会被不需要的高频信号所污染,同时保留了大部分所需信号.
高斯函数傅立叶变换等于高斯函数本身的证明可自行查找资料

4).高斯滤波器宽度(决定着平滑程度)是由参数σ表征的,而且σ和平滑程度的关系是非常简单的.σ越大,高斯滤波器的频带就越宽,平滑程度就越好.通过调节平滑程度参数σ,可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(欠平滑)之间取得折衷.
5).由于高斯函数的可分离性,较大尺寸的高斯滤波器可以得以有效地实现.二维高斯函数卷积可以分两步来进行,首先将图像与一维高斯函数进行卷积,然后将卷积结果与方向垂直的相同一维高斯函数卷积.因此,二维高斯滤波的计算量随滤波模板宽度成线性增长而不是成平方增长.
高斯滤波应用
高斯滤波后图像被平滑的程度取决于标准差.它的输出是领域像素的加权平均,同时离中心越近的像素权重越高.因此,相对于均值滤波(mean filter)它的平滑效果更柔和,而且边缘保留的也更好.
高斯滤波被用作为平滑滤波器的本质原因是因为它是一个低通滤波器(其频谱图如上节所示).而且,大部份基于卷积平滑滤波器都是低通滤波器.
参考资料
1.图像滤波之高斯滤波介绍
2.图像处理基础(4):高斯滤波器详解
3.简单易懂的高斯滤波
4.线性滤波、非线性滤波区别
5.如何确定高斯滤波的标准差和窗口大小
6.二维图像处理中的可分离卷积核
7.可分离卷积的运算量比较与分析(一维、二维卷积)
8.关于高斯滤波的一些理解
附录
高斯函数及频谱绘图代码
绘制高斯函数曲线代码:
一维高斯函数:
from matplotlib import pyplot as plt
import numpy as np
def gaussian(x, mu, sig):
a = 1 / (np.sqrt(2 * np.pi) * sig)
return a*np.exp(-np.power(x - mu, 2.) / (2 * np.power(sig, 2.)))
x_values = np.linspace(-11, 11, 120)
for mu, sig in [(0, 1), (0, 2), (0, 3)]:
plt.plot(x_values, gaussian(x_values, mu, sig),label='σ={}'.format(sig))
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='best')
plt.grid(linestyle='--')
plt.show()
二维高斯函数:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x,y = np.meshgrid(np.arange(-5,5,0.1),np.arange(-5,5,0.1))
sigma = 1
z = 1/(2 * np.pi * (sigma**2)) * np.exp(-(x**2+y**2)/(2 * sigma**2))
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow',alpha = 0.9)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
# plt.title("二维高斯分布")
plt.show()
绘制高斯傅里叶变换频谱:
# Reference:https://www.cnblogs.com/jingsupo/p/9989559.html
import numpy as np#导入一个数据处理模块
import pylab as pl#导入一个绘图模块,matplotlib下的模块
def gaussian(x, mu, sig):
a = 1 / (np.sqrt(2 * np.pi) * sig)
return a*np.exp(-np.power(x - mu, 2.) / (2 * np.power(sig, 2.)))
sampling_rate = 8000#采样频率为8KHz
fft_size = 8000 #FFT处理的取样长度
t = np.arange(0, 4.0, 1.0/sampling_rate)#np.arange(起点,终点,间隔)产生4s长的取样时间
x = gaussian(t,0,1)
xs = x[:fft_size]# 从波形数据中取样fft_size个点进行运算
xf = np.fft.rfft(xs)# 利用np.fft.rfft()进行FFT计算,rfft()是为了更方便对实数信号进行变换,由公式可知/fft_size为了正确显示波形能量
xf = xf / len(xf)
# rfft函数的返回值是N/2+1个复数,分别表示从0(Hz)到sampling_rate/2(Hz)的分.
#于是可以通过下面的np.linspace计算出返回值中每个下标对应的真正的频率:
freqs = np.linspace(0, sampling_rate/2, fft_size//2+1)#频率
xfp = np.abs(xf)#幅值
#绘图显示结果
pl.figure(figsize=(8,4))
pl.subplot(211)
pl.plot(t, x)
pl.xlim(0,)
pl.ylim(0,)
pl.xlabel('t')
pl.title('Gaussias\'s WaveForm And Freq')
pl.subplot(212)
freqs = freqs[:100]
xfp = xfp[:100]
_range = np.max(xfp) - np.min(xfp)
xfp=(xfp - np.min(xfp)) / _range
pl.plot(freqs, xfp)
pl.xlim(0,)
pl.ylim(0,)
pl.xlabel('Freq/Hz')
pl.ylabel('Amplitude')
pl.subplots_adjust(hspace=0.4)
pl.show()

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容








所有评论(0)