【计算机视觉----相机标定】
相机标定是计算机视觉中的一个重要问题,它的目的是确定相机的内部参数和外部参数,以建立从相机到图像的映射关系。相机标定的算法通常分为两个步骤:第一步是检测棋盘格角点并计算相机的内部参数,第二步是计算相机的外部参数。第一步:检测棋盘格角点并计算相机的内部参数棋盘格标定法是一种常用的相机标定方法,它基于在棋盘格上已知的角点坐标和实际测量的角点在图像中的位置,通过最小化重投影误差来求解相机的内部参数。具体
相机标定
相机标定内容
相机标定是计算机视觉中的一个重要问题,它的目的是确定相机的内部参数和外部参数,以建立从相机到图像的映射关系。相机标定的算法通常分为两个步骤:第一步是检测棋盘格角点并计算相机的内部参数,第二步是计算相机的外部参数。
第一步:检测棋盘格角点并计算相机的内部参数
棋盘格标定法是一种常用的相机标定方法,它基于在棋盘格上已知的角点坐标和实际测量的角点在图像中的位置,通过最小化重投影误差来求解相机的内部参数。具体步骤如下:
- 选择一个棋盘格图案,并测量棋盘格的大小和格点数量。
- 在不同的方向、距离和角度下拍摄多张包含棋盘格的图片,并将图片转换为灰度图。
- 对每张图片中的棋盘格进行角点检测,得到角点的像素坐标。
- 将每张图片中的角点像素坐标与棋盘格中的角点物理坐标对应起来,得到相机的内部参数矩阵和畸变系数。
- 使用Levenberg-Marquardt算法最小化重投影误差,得到相机的内部参数矩阵和畸变系数的最优解。
第二步:计算相机的外部参数
在得到相机的内部参数后,可以使用PnP算法计算相机的外部参数。PnP算法是一种基于3D-2D点对的相机姿态估计算法,根据已知的3D点和它们在图像中的对应2D点,计算相机的旋转向量和平移向量,即相机的外部参数。具体步骤如下:
- 确定一组已知的3D点和它们在图像中的对应2D点。
- 根据相机的内部参数矩阵和畸变系数,将2D点坐标转换为归一化相机坐标系下的坐标。
- 使用PnP算法求解相机的旋转向量和平移向量,即相机的外部参数。
在实际应用中,相机标定通常需要采集多张图像,并进行角点检测和匹配,然后使用标定算法计算相机的内部参数和外部参数。OpenCV中提供了相机标定的函数,可以方便地实现相机标定功能。例如,cv2.calibrateCamera()函数可以根据一组已知的3D点和它们在图像中的对应2D点,计算相机的内部参数和畸变系数,同时也可以计算相机的外部参数。
相机标定原理
基本原理
相机标定的原理是利用相机成像的知识,通过对多张已知场景的图片进行分析,从而估算出相机的内部参数矩阵和畸变系数,进而估算出相机的外部参数。
相机的内部参数矩阵包含了相机的焦距、光心位置、像素宽高比等参数,是一个3×3的矩阵,可以表示为:
fx 0 cx
0 fy cy
0 0 1
其中,fx和fy表示相机在x轴和y轴方向上的焦距,cx和cy表示相机光心的像素坐标。当相机的内部参数矩阵确定后,就可以通过将3D场景中的点投影到2D图像平面上,计算出它在图像中的像素坐标。
相机的畸变系数包括径向畸变和切向畸变两个部分。径向畸变是由于相机镜头的物理结构而导致的,使得图像中心和边缘的像素不在同一平面上,从而引起图像中心处的放大和边缘处的收缩,表现为图像中心向外凸出。切向畸变是由于相机镜头和图像平面不平行而产生的,表现为图像中心处的像素不在同一水平线上。
相机标定的基本原理是通过拍摄多张包含已知场景的图片,对每张图片中的角点进行检测和匹配,然后利用这些角点的图像坐标和3D场景中的物理坐标,求解相机的内部参数矩阵和畸变系数。
在确定相机的内部参数之后,可以使用PnP算法计算相机的外部参数。PnP算法是一种基于3D-2D点对的相机姿态估计算法,根据已知的3D点和它们在图像中的对应2D点,计算相机的旋转向量和平移向量,进而得到相机的外部参数。同时,也可以使用双目视觉或多目视觉等技术,通过多个相机之间的匹配,计算出相机的外部参数和场景的三维结构。
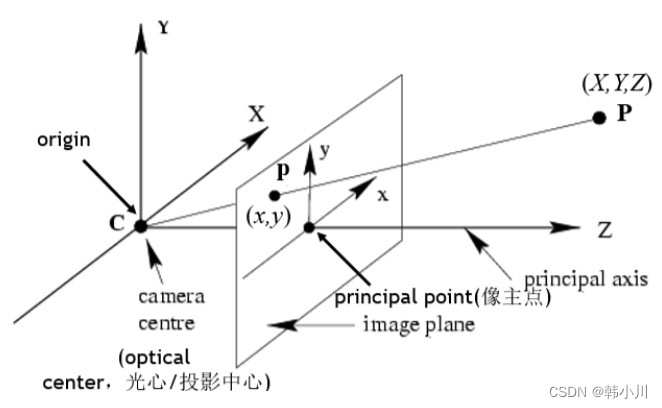
针孔相机成像原理其实就是利用投影将真实的三维世界坐标转换到二维的相机坐标上去,其模型示意图如下图所示:

从图中我们可以看出,在世界坐标中的一条直线上的点在相机上只呈现出了一个点,其中发生了非常大的变化,同时也损失和很多重要的信息,这正是我们3D重建、目标检测与识别领域的重点和难点。实际中,镜头并非理想的透视成像,带有不同程度的畸变。理论上镜头的畸变包括径向畸变和切向畸变,切向畸变影响较小,通常只考虑径向畸变。
相机标定的作用
(1)一个是由于每个镜头的在生产和组装过程中的畸变程度各不相同,通过相机标定可以校正这种镜头畸变,生成矫正后的图像——矫正透镜畸变;
(2)另一个是根据标定后的到的相机参数建立相机成像几何模型,由获得的图像重构出三维场景。具体来说:当我们用摄像机拍照时,从照片里得到一些空间信息(比如距离,尺寸等),是要利用二维图像得到三维信息。我们拍照的时候把空间物体信息通过摄像机变成了二维图像,这个过程本来是不可逆的。但如果我们可以找到一个摄像机的数学模型,就可以 :从二维图像+模型逆推得到原来三维信息。标定就是在找这个模型。

相机标定实际应用
- 相机在出厂之前都需要进行相机标定,用软件的方法校正生成的图像,避免拍摄出的图像产生桶形和枕形畸变;

- 根据相机成像的几何模型,将世界坐标系中的3D物体映射到2D成像平面上;
- 求解多个相机对之间的映射关系。
相机标定后结果
- 相机的内参矩阵 A ( d x , d y , r , u , v , f ) A(dx, dy, r, u, v, f) A(dx,dy,r,u,v,f),外参矩阵 [ R ∣ T ] [R|T] [R∣T]、畸变系数 [ k 1 , k 2 , k 3 , p 1 , p 2 ] [k1, k2, k3, p1, p2] [k1,k2,k3,p1,p2]。
- 内参矩阵各元素意义:一个像素的物理尺寸 d x dx dx和 d y dy dy,焦距 f f f,图像物理坐标的扭曲因子 r r r,图像原点相对于光心成像点的的纵横偏移量 u u u和 v v v(像素为单位)。
- 外参矩阵: 世界坐标系转换到相机坐标系的旋转 R R R和平移 T T T矩阵。
- 畸变系数: 包括相机的径向畸变系数
k
1
,
k
2
,
k
3
k1, k2, k3
k1,k2,k3和相机的切向畸变系数
p
1
,
p
2
p1, p2
p1,p2。

张正友黑白棋盘格标定法(Zhang’s calibration method)
张正友黑白棋盘格标定法是一种基于棋盘格的相机标定方法,由张正友教授在1999年提出。这种方法通过使用黑白相间、大小固定的棋盘格来检测相机的内部参数和畸变系数,具有简单易行、精度高等优点。
棋盘格标定法的基本原理是在已知棋盘格的物理坐标和图像坐标的情况下,利用相机的内部参数和畸变系数,建立从物理坐标到图像坐标的映射关系。
张正友标定法利用黑白棋盘格标定板,在得到一张标定板的图像之后,用Harris角点检测算法得到每一个角点的像素坐标 ( u , v ) (u,v) (u,v)。
张正友标定法将世界坐标系固定于棋盘格上,则棋盘格上任一点的物理坐标W=0,由于标定板的世界坐标系是人为事先定义好的,标定板上每一个格子的大小是已知的,我们可以计算得到每一个角点在世界坐标系下的物理坐标 ( U , V , W = 0 ) (U,V,W=0) (U,V,W=0)。
我们将利用这些信息:每一个角点的像素坐标、每一个角点在世界坐标系下的物理坐标,来进行相机的标定,获得相机的内外参矩阵、畸变参数。
算法步骤
单应性矩阵H
单应性:在计算机视觉中被定义为一个平面到另一个平面的投影映射。首先确定,图像平面与标定物棋盘格平面的单应性。
设三维世界坐标的点为
X
=
[
X
,
Y
,
Z
,
1
]
T
X=[X, Y, Z, 1]^T
X=[X,Y,Z,1]T,二维相机平面像素坐标为
m
=
[
u
,
v
,
1
]
T
m=[u, v,1]^T
m=[u,v,1]T,所以标定用的棋盘格平面到图像平面的单应性关系为:
s
0
m
=
K
[
R
∣
T
]
X
s_0m=K[R|T]X
s0m=K[R∣T]X (其中,
K
K
K为相机的内参矩阵,
R
R
R为外部参数矩阵(旋转矩阵),
T
T
T为平移向量。令:
K
=
[
α
γ
u
0
0
β
v
0
0
0
1
]
\begin{equation} K={\left[ \begin{array}{ccc} \alpha & \gamma & u_0\\ 0 & \beta & v_0\\ 0 & 0 & 1 \end{array} \right ]} \end{equation}
K=
α00γβ0u0v01
Z
=
0
Z=0
Z=0的平面,定义旋转矩阵
R
R
R的第
i
i
i列为
r
i
r_i
ri, 则有:
s
[
u
v
1
]
=
K
[
r
1
r
2
r
3
t
]
[
X
Y
0
1
]
=
K
[
r
1
r
2
t
]
[
X
Y
1
]
\begin{equation} s{\left[ \begin{array}{ccc} u \\ v \\ 1 \end{array} \right ]}=K{\left[ \begin{array}{ccc} r_1 & r_2 & r_3 & t \end{array} \right ]}{\left[ \begin{array}{ccc} X \\ Y \\ 0 \\ 1 \end{array} \right ]}= K{\left[ \begin{array}{ccc} r_1 & r_2 & t \end{array} \right ]}{\left[ \begin{array}{ccc} X \\ Y \\ 1 \end{array} \right ]} \end{equation}
s
uv1
=K[r1r2r3t]
XY01
=K[r1r2t]
XY1
于是空间到图像的映射可改为:
H
=
λ
K
[
r
1
r
2
t
]
H=λK{\left[ \begin{array}{ccc}r_1&r_2&t\end{array} \right ]}
H=λK[r1r2t]。其中
H
H
H是描述
H
o
m
o
g
r
a
p
h
i
c
Homographic
Homographic矩阵,可通过最小二乘,从角点世界坐标到图像坐标的关系求解。
内参数矩阵
根据步骤1中的式子,令
H
H
H为
H
=
[
h
1
h
2
h
3
]
H ={\left[ \begin{array}{ccc}h_1&h_2&h_3\end{array} \right ]}
H=[h1h2h3],则
[
h
1
h
2
h
3
]
=
λ
K
[
r
1
r
2
t
]
{\left[ \begin{array}{ccc}h_1&h_2&h_3\end{array} \right ]}=λK{\left[ \begin{array}{ccc}r_1&r_2&t\end{array} \right ]}
[h1h2h3]=λK[r1r2t],再根据正交和归一化的约束可以得到等式:
h
1
T
A
−
T
A
−
1
h
2
=
0
\ h_1^TA^{-T}A^{-1}h_2=0
h1TA−TA−1h2=0
h
1
T
A
−
T
A
−
1
h
1
=
h
2
T
A
−
T
A
−
1
h
2
\ h_1^TA^{-T}A^{-1}h_1=h_2^TA^{-T}A^{-1}h_2
h1TA−TA−1h1=h2TA−TA−1h2
即每个单应性矩阵能提供两个方程,而内参数矩阵包含5个参数,要求解,至少需要3个单应性矩阵。为了得到三个不同的单应性矩阵,我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到三个不同的图片。为了方便计算,我们定义:
B
=
A
−
T
A
−
1
=
[
B
11
B
21
B
31
B
12
B
22
B
32
B
13
B
23
B
33
]
=
[
1
α
2
−
γ
α
2
β
v
0
γ
−
u
0
β
α
2
β
−
γ
α
2
β
γ
α
2
β
2
+
1
β
2
−
γ
(
v
0
γ
−
u
0
β
)
α
2
β
2
−
v
0
2
β
2
v
0
γ
−
u
0
β
α
2
β
−
γ
(
v
0
γ
−
u
0
β
)
α
2
β
2
−
v
0
2
β
2
(
v
0
γ
−
u
0
β
)
2
α
2
β
2
+
v
0
2
β
2
+
1
]
\begin{equation} B= A^{-T}A^{-1}={\left[ \begin{array}{ccc} B_{11} & B_{21} & B_{31}\\ B_{12} & B_{22} & B_{32}\\ B_{13} & B_{23} & B_{33} \end{array} \right ]}={\left[ \begin{array}{ccc} \frac{1} {\alpha^2} & -\frac{\gamma} {\alpha^2\beta} & \frac{v_0\gamma-u_0\beta} {\alpha^2\beta}\\ -\frac{\gamma} {\alpha^2\beta} &\frac{\gamma} {\alpha^2\beta^2}+\frac{1} {\beta^2} &- \frac{\gamma(v_0\gamma-u_0\beta)} {\alpha^2\beta^2}-\frac{v_0^2} {\beta^2}\\ \frac{v_0\gamma-u_0\beta} {\alpha^2\beta}& -\frac{\gamma(v_0\gamma-u_0\beta)} {\alpha^2\beta^2}-\frac{v_0^2} {\beta^2}&\frac{(v_0\gamma-u_0\beta)^2} {\alpha^2\beta^2}+\frac{v_0^2} {\beta^2}+1 \end{array} \right ]} \end{equation}
B=A−TA−1=
B11B12B13B21B22B23B31B32B33
=
α21−α2βγα2βv0γ−u0β−α2βγα2β2γ+β21−α2β2γ(v0γ−u0β)−β2v02α2βv0γ−u0β−α2β2γ(v0γ−u0β)−β2v02α2β2(v0γ−u0β)2+β2v02+1
B
B
B中的未知量可表示为
6
D
6D
6D向量
b
b
b,
b
=
[
B
11
B
12
B
22
B
13
B
23
B
33
]
T
b={\left[ \begin{array}{ccc}B_{11}&B_{12}&B_{22}&B_{13}&B_{23}&B_{33}\end{array} \right ]}^T
b=[B11B12B22B13B23B33]T
设
H
H
H中的第
i
i
i列为
h
i
h_i
hi,
h
i
=
[
h
i
1
h
i
2
h
i
3
]
T
h_i ={\left[ \begin{array}{ccc}h_{i1}&h_{i2}&h_{i3}\end{array} \right ]}^T
hi=[hi1hi2hi3]T,根据b的定义,可以推导出公式:
h
i
B
h
j
=
v
i
j
T
b
h_iBh_j=v_{ij}^Tb
hiBhj=vijTb,
v
i
j
=
[
h
i
1
h
j
1
h
i
1
h
j
2
+
h
i
2
h
j
1
h
i
2
h
j
2
h
i
3
h
j
1
+
h
i
1
h
j
3
h
i
3
h
j
2
+
h
i
2
h
j
3
h
i
3
h
j
3
]
T
v_{ij}={\left[ \begin{array}{ccc}h_{i1}h_{j1}&h_{i1}h_{j2}+h_{i2}h_{j1}&h_{i2}h_{j2}&h_{i3}h_{j1}+h_{i1}h_{j3}&h_{i3}h_{j2}+h_{i2}h_{j3}&h_{i3}h_{j3}\end{array} \right ]}^T
vij=[hi1hj1hi1hj2+hi2hj1hi2hj2hi3hj1+hi1hj3hi3hj2+hi2hj3hi3hj3]T
最后推导出
[
v
12
T
(
v
11
−
v
12
)
T
]
b
=
0
{\left[ \begin{array}{ccc} v_{12}^T \\ (v_{11}-v_{12})^T \end{array} \right ]}b=0
[v12T(v11−v12)T]b=0,通过上式,我们可知当观测平面
n
≥
3
n ≥ 3
n≥3时,即至少3幅棋盘格图像,可以得到
b
b
b的唯一解,求得相机内参数矩阵
K
K
K。
外参数矩阵
外部参数可通过 H o m o g r a p h y Homography Homography求解,由 H = [ h 1 h 2 h 3 ] = λ A [ r 1 r 2 t ] H ={\left[ \begin{array}{ccc}h_1&h_2&h_3\end{array} \right ]}= λA{\left[ \begin{array}{ccc}r_1&r_2&t\end{array} \right ]} H=[h1h2h3]=λA[r1r2t],可推出 r 1 = λ A − 1 h 1 r_1=λA^{-1}h_1 r1=λA−1h1, r 2 = λ A − 1 h 2 r_2=λA^{-1}h_2 r2=λA−1h2, r 3 = r 1 ∗ r 2 r_3=r_1*r_2 r3=r1∗r2, t = λ A − 1 h 3 t=λA^{-1}h_3 t=λA−1h3
最大似然估计
上述的推导结果是基于理想情况下而言,但由于可能存在一些其他干扰,所以使用最大似然估计进行优化。假设拍摄了n张棋盘格图像,每张图像有m个角点。最终获得的最大似然估计公式为:
∑
i
=
1
n
∑
j
=
1
m
∣
∣
m
i
j
−
m
^
(
A
,
R
i
,
t
i
,
M
j
)
∣
∣
2
\sum_{i=1}^n\sum_{j=1}^m||m_{ij}-\hat{m}(A,R_i,t_i,M_j)||^2
i=1∑nj=1∑m∣∣mij−m^(A,Ri,ti,Mj)∣∣2
实验过程
实验步骤
- 取材:打印一张棋盘格,把它贴在一个平面上,作为标定物,通过调整标定物或摄像机 的方向,为标定物拍摄一些不同方向的照片。
- 从照片中提取棋盘格角点。
- 估算理想无畸变的情况下,五个内参和六个外参。
- 应用最小二乘法估算实际存在径向畸变下的畸变系数。
- 极大似然法,优化估计,提升估计精度。
实验数据

实验代码
import cv2
import numpy as np
import glob
# 设置寻找亚像素角点的参数,采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# 获取标定板角点的位置
objp = np.zeros((4*4, 3), np.float32)
objp[:, :2] = np.mgrid[0:4, 0:4].T.reshape(-1, 2) # 将世界坐标系建在标定板上,所有点的Z坐标全部为0,所以只需要赋值x和y
obj_points = [] # 存储3D点
img_points = [] # 存储2D点
images = glob.glob(r"/Users/hanjingliu/workspace/daily/course/computer_vision/xiangjibiaoding/*.jpg")
# print(images)
i = 0
for fname in images:
# print(fname)
img = cv2.imread(fname)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
size = gray.shape[::-1]
ret, corners = cv2.findChessboardCorners(gray, (4, 4), None)
# print(corners)
if ret:
obj_points.append(objp)
corners2 = cv2.cornerSubPix(gray, corners, (1, 1), (-1, -1), criteria) # 在原角点的基础上寻找亚像素角点
#print(corners2)
if [corners2]:
img_points.append(corners2)
else:
img_points.append(corners)
cv2.drawChessboardCorners(img, (4, 4), corners, ret) # 记住,OpenCV的绘制函数一般无返回值
i += 1
cv2.imwrite('conimg'+str(i)+'.jpg', img)
cv2.waitKey(4000)
print(len(img_points))
cv2.destroyAllWindows()
# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)
print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist) # 畸变系数 distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs) # 旋转向量 # 外参数
print("tvecs:\n", tvecs) # 平移向量 # 外参数
print("-----------------------------------------------------")
img = cv2.imread(images[10])
print(images[10])
h, w = img.shape[:2]
# 获取新的相机矩阵和ROI
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w, h), 1, (w, h)) # 显示更大范围的图片(正常重映射之后会删掉一部分图像)
print(newcameramtx)
print("------------------使用undistort函数-------------------")
# 进行畸变校正
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)
x, y, w, h = roi
dst1 = dst[y:y+h, x:x+w]
# 保存校正后的图片
cv2.imwrite('calibresult1.jpg', dst1)
print("dst的大小为:", dst1.shape)
实验运行结果
12
ret: 3.731461151302655
mtx:
[[1.96480060e+03 0.00000000e+00 7.60254618e+02]
[0.00000000e+00 2.17238853e+03 6.18328246e+02]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
dist:
[[-7.17465676e-01 1.77558904e+01 -2.87353021e-02 -8.53489073e-03
-1.02909372e+02]]
rvecs:
(array([[0.60476237],
[0.09121906],
[0.59630672]]), array([[-5.69794620e-01],
[-1.38765746e-06],
[ 3.60910567e-02]]), array([[-0.48821515],
[-0.62488527],
[-1.51741133]]), array([[-0.87227468],
[-0.27566804],
[-0.9381464 ]]), array([[-0.41077245],
[ 0.80494707],
[ 1.57063136]]), array([[-0.5147985 ],
[-0.57966852],
[ 0.13310587]]), array([[ 0.28565288],
[-0.43624729],
[ 0.72698007]]), array([[-0.78497379],
[-0.07024525],
[-0.00114507]]), array([[-0.82910917],
[-0.29652805],
[-0.68373933]]), array([[-0.2162998 ],
[-0.60518062],
[-1.5425057 ]]), array([[-0.43803419],
[ 0.57275538],
[ 0.39879017]]), array([[-0.15128549],
[ 0.03192674],
[-0.00145978]]))
tvecs:
(array([[ 2.34189354],
[-0.09515954],
[13.86982558]]), array([[-1.12291722],
[-1.12916636],
[15.28226729]]), array([[-2.60274398],
[ 1.23832444],
[14.98524274]]), array([[-1.58071137],
[-0.94452542],
[16.11396534]]), array([[ 2.7992926 ],
[-2.53093362],
[15.80095039]]), array([[-1.19873162],
[-1.64378981],
[28.55703926]]), array([[-0.83237304],
[-0.385658 ],
[14.64918988]]), array([[-2.28757939],
[-2.3488313 ],
[15.76002841]]), array([[-2.71934002],
[-0.91544196],
[14.27312879]]), array([[-3.29920121],
[ 0.22711141],
[23.66953694]]), array([[-4.0087668 ],
[-3.74323286],
[24.92407857]]), array([[-2.27554136],
[-0.33247034],
[12.63636645]]))
-----------------------------------------------------
/Users/hanjingliu/workspace/daily/course/computer_vision/xiangjibiaoding/3.jpg
[[1.11144873e+03 0.00000000e+00 4.30060960e+02]
[0.00000000e+00 1.31612244e+03 1.04604358e+03]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
------------------使用undistort函数-------------------
dst的大小为: (1022, 723, 3)

实验结果分析
* 可以标定出相机的畸变参数,内参矩阵,外参矩阵对相机进行参数调整,从而完成畸变校正。
+ 畸变参数:计算机在径向和切向的畸变程度
+ 内参矩阵:一个像素的物理尺寸dx和dy,焦距 f,图像物理坐标的扭曲因子r,图像原点相对于光心成像点的的纵横偏移量u和 v。
+ 外参矩阵:世界坐标转换成相机坐标系的旋转和平移矩阵。
* 把打印的棋盘纸张贴在平板上,拍出来的照片和显示图像及物理点和世界点存在的误差才会理想,找一个光线较暗不会造成拍摄反光的地方对图片进行拍摄,可以有效减小误差。
* 从实验结果可以看出,mtx为内参矩阵,dist为畸变系数,外参数为rvecs(旋转向量)和tvecs(平移向量)。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)