相机标定是获得目标工件精准坐标信息的基础。首先，必须进行相机内参标定，构建一个模型消除图像畸变；其次，需要对相机和机器人的映射关系进行手眼标定，构建一个模型将图像坐标系上的点映射到世界坐标系。主要分为背景知识、相机内外参模型推导、编程代码实现三个部分。

1 背景知识

        在讨论相机模型标定之前，我们应当先了解几何里面关于2D、3D空间里面几种几何变换形式。主要包括欧式变换、相似变换、仿射变换和透视变换，相机标定的过程，就是一个透视变换矩阵求解的过程。

参考来源：北京邮电大学鲁鹏老师的课件

1.1 2D平面上的变换

1.1.1 欧式变换

        所谓欧式变换，即只有平移加旋转的变换，例如在2D平面上有一个正方形，经过变换后正方形的尺寸没有发生改变，但中心点会发生改变，并且偏转了一定的角度。自由度为三个，即xy方向的平移和旋转的角度theta。

1.1.2 相似变换

        所谓的相似变换，即在欧式变换的基础上，附加一个均匀伸缩变换。经过变换后，在相似变换的基础上对原有的尺寸进行了放缩。但保证线与线之间的角度、长度的比值和面积的比值不变。自由度为四个：即xy方向的平移和旋转的角度再加一个放缩系数。

 1.1.3 仿射变换

        所谓的仿射变换，即在相似变换的基础上再增加了两个自由度。由上图的相似变换矩阵可以得知，决定矩阵数值的值主要有s、θ、X0、Y0。我们可以看到s、θ两个参数决定了矩阵里面的四个数值，假设这四个参数完全由a、b、c、d四个独立的变量进行控制，即仿射变换一共有六个自由度。变换前后线与线之间的平行性、平行线段长度的比值和面积的比值不变。

1.1.3 透视变换

        所谓的透视变换，即在仿射变换的基础上再次增加两个自由度，由仿射变换的矩阵我们可以看到，其第三行两个数值都为0，假设其不为0，分别为V1、V2。因此，透视变换一共有八个自由度，变换前后只有四共线的交比保持不变，即交比不变性。

1.2 3D空间上的变换

1.2.1 欧式变换

        所谓欧式变换，即只有平移加旋转的变换。当其在三维空间里面时，旋转共有绕三个轴xyz的旋转，平移也是发生在三维空间。同时在此基础上附加一个放缩系数s，其一共有七个自由度，变换前后不变量：点变换到点、线变换到线；保持点的共线性、线的共面性；保持直线与直线、直线与平面、平面与平面的平行性不变；保持线的夹角不变。

三维空间旋转平移变换可参考：机器人学导论

 1.2.2 仿射变换

        三维空间的仿射变换，在上面欧式变换的基础上进一步增加自由度。由欧式变换的上图可知，其中R旋转矩阵由绕三个XYZ轴旋转的角度决定的。R矩阵是一个3×3的矩阵，当里面九个参数互相独立时，就是三维空间的仿射变换。其一共有12个自由度，变换前后的不变量：保持无穷远平面不变（无穷远点变换到无穷远点），保持直线与直线、直线与平面、平面与平面的平行性不变。

 1.2.3 透视变换

        三维空间的透视变换，可以看到上面仿射变换矩阵主要由矩阵A、向量t、向量0和1组成。因为A为一个3×3的矩阵，所以向量0是一个三维向量。如果这个向量不为0，为三个独立的数值构成的向量。则透视变换矩阵在仿射变换矩阵的基础上再次增加了三个自由度，其一共有十五个自由度，变换前后的不变量有：点变换到点、线变换到线，保持点的共线性和线的共面性。

        综上所述，经过透视变换后，线的平行性不再保持，这也引申出影消点和影消线的概念，即在实际空间中，互相平行的铁轨，变换到图像里，会相交于一点。由这些点组成的线就是影消线。

基于影消线和影消点，可以实现三维重建，这里不再赘述。

鲁鹏老师三维重建课程之单视图重建https://blog.csdn.net/beyond951/article/details/122265206?spm=1001.2014.3001.5501

2 相机内外参模型推导

2.1 相机外参

        在三维空间中，准确描述执行器的状态，需要包括执行器的位置信息和姿态信息。齐次变换矩阵在机器人学中描述一个坐标系到另一个坐标系变换关系的矩阵，包括位姿的旋转分量和平移分量。

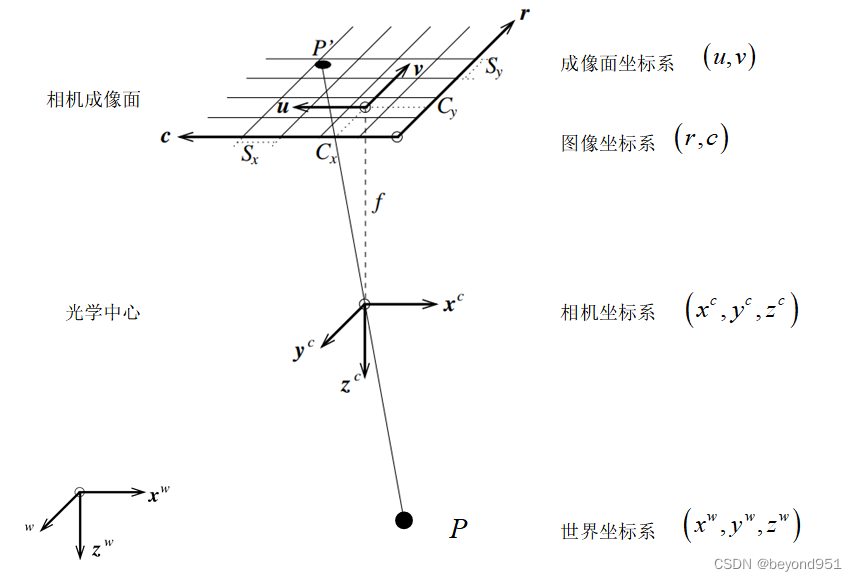
         相机小孔成像模型

        如图上图所示，显示了针孔相机成像的透视投影模型。世界点P通过透镜的光学中心投射到像面上的点P'，点位于光学中心后面距离(焦距)f处。基于该投影模型，可以描述物体在世界坐标系中的点映射到图像平面和相应的相机参数。

        世界坐标系变换到相机坐标系

       如图上图所示，先确定点 P是在世界坐标系WCS中，为确定世界坐标系映射到图像坐标系的关系，需要先转换成相机坐标系CCS。定义CCS，使其x轴和y轴分别平行于图像的c轴和r轴，z轴垂直于图像平面。其可以用位姿进行描述，也可以用齐次变换矩阵cwH表示。因此，相机坐标系点Pc(Xc,Yc,Zc)可由世界坐标系Pw(Xw,Yw,Zw)变换得到：

 2.2 相机内参

        假设成像面位于光心前面距离为f的位置，如下图所示。

        接下来，将相机坐标系CCS的点(Xc,Yc,Zc)投影到图像坐标系。对于针孔相机模型，投影为透视投影，由此可得：

        对于远心相机模型，透视为平行投影，此时，没有焦距，f近似于无穷远，由此可得：

 （1）畸变矫正

        相机在加工过程中，由于各类非线性因素的影响，会存在一定的误差，从而造成镜头畸变。导致视觉系统获取的图像与实际图像之间产生差别。不同相机产生的畸变情况也会有差异，在制造装配过程中产生的误差，造成图像径向畸变比较严重。

        坐标点投影到成像面后，畸变会造成成像面上的点qc(u,v)偏移至qc'(u',v')。其效果图如下图所示，如果没有畸变存在的情况下，成像面上P‘应投影在点P和光学中心延长线与成像面的交点处。相机畸变的存在造成P在不同的位置。相机畸变是一种可以单独在图像平面上建模的变换，畸变可以用出发模型或多项式模型来建模。

        除法模型使用一个参数k来模拟径向变形。基于除法模型，通过下面的方程表示相机的畸变模型。

        这些方程可以通过解析的方法进行反求，如果采用除法模型，则会得到下列方程，将未有畸变的坐标转化为畸变的坐标，其解析解如下：

        参数k用来模拟径向变形的大小。如果k为负，则扭曲为桶形，而k为正，则扭曲为枕形。其变形如图所示。

        多项式模型使用三个参数（K1,K2,K3）来模拟径向畸变，两个参数（P1,P2）来模拟扭转变形。下面的多项式模型可以将失真的像平面坐标转换为未失真的像平面坐标。

        该模型不能用解析法进行反求。因此，失真图像平面坐标必须从未失真图像平面坐标数值计算出来。综上考虑，本文采用多项式模型对相机获取的图像进行矫正，最终可以得到5个畸变参数K1,K2,K3,P1,P2。

编程代码实现

基于Halcon标定

        基于halcon标定主要是采集完图像后运用halcon的标定助手对相机内外参进行标定。采集到的图像如下图所示：

标定后的内外参为：

标定后的外参为：

基于OpenCV标定

用于标定的图像：

标定的程序代码：

void Cam_Calib()
{
	Creat_CalibImg_Path();
	vector<string> Img_Vec;
	char dir[64];
	char fileNames[64];
	ofstream fout(calibrationResult);  //保存标定结果的文件
	// 利用dir命令将当前目录下的.bmp文件名写入names.txt
	sprintf(dir, "%s%s%s%s%s%s", "dir ", chess_boardImage_path, "*.bmp", " /a /b >", chess_boardImage_path, "names.txt");
	system(dir);
	char name[64] = "";
	// 打开文件读取其中的文件名
	sprintf(fileNames, "%s%s", chess_boardImage_path, "names.txt");
	FILE* fp = fopen(fileNames, "r");

	if (NULL == fp)
	{
		printf("error,cannot open the name list");
	}
	while (fgets(name, 64, fp) != NULL)
	{
		char subname[64];
		sscanf(name, "%[^\n]%s", subname);
		string image_name;
		stringstream stream;
		stream << subname;
		image_name = stream.str();
		Img_Vec.push_back(image_name.substr(0, image_name.length() - 4));
	}

	//角点提取
	cout << "角点提取………………" << endl;
	vector<Mat>  image_Seq;                  //检测到角点图片
	vector<vector<Point2f>>  corners_Seq;    //保存检测到的所有角点
	int Num = Img_Vec.size();
	for (int i = 0; i < Num; i++)
	{
		cout << "图像 #" << Img_Vec[i] << "..." << endl;
		string imageFileName;
		imageFileName = Img_Vec[i];     //图像的文件名
		imageFileName += ".bmp";       //图像的文件名.bmp
		Mat image = imread(chess_boardImage_path + imageFileName);
		vector<Point2f> corners1 = Api.Get_Conners(image, Conner_Size, chess_boardCorner_path + Img_Vec[i], 0);
		if (corners1.size() == Conner_Size.width*Conner_Size.height)
		{
			corners_Seq.push_back(corners1);
			image_Seq.push_back(image);
			cout << "Frame corner #" << Img_Vec[i] << "success" << endl;
		}
		else
		{
			cout << "can not find chessboard corners!\n";
		}
	}
	if (image_Seq.size() <= 0)  return;
	cout << "共提取" << image_Seq.size() << "张图像角点！\n";

	//摄像机标定
	cout << "开始标定………………" << endl;
	vector<vector<Point3f>>  object_Points = Api.Get_CalibCoord_Points(Real_Size, image_Seq.size(), Conner_Size);

	calibrateCamera(object_Points, corners_Seq, image_Seq[0].size(), intrinsic_matrix, distortion_coeffs, rotation_vectors, translation_vectors, CV_CALIB_FIX_K3, cv::TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 50, 1e-6));  //CV_CALIB_FIX_K3
	cout << "标定完成！\n";
	cout << "每幅图像的标定误差：" << endl;
	double total_err = 0.0;                   //所有图像的平均误差的总和	

	for (int i = 0; i < image_Seq.size(); i++)
	{
		double err = Api.Calib_Error(object_Points[i], corners_Seq[i], intrinsic_matrix, distortion_coeffs, rotation_vectors[i], translation_vectors[i]);
		total_err += err /= object_Points[i].size();
		cout << "图 " << Img_Vec[i] << " 的平均误差：" << err << "像素" << endl;
		fout << "图 " << Img_Vec[i] << " 的平均误差：" << err << "像素" << endl;
	}
	cout << "总体平均误差：" << total_err / image_Seq.size() << "像素" << endl;
	fout << "总体平均误差：" << total_err / image_Seq.size() << "像素" << endl << endl;
	cout << "评价完成！" << endl;

	//保存标定结果
	cout << "开始保存标定结果………………" << endl;
	Mat rotation_matrix = Mat(3, 3, CV_32FC1, Scalar::all(0)); //保存每幅图像的旋转矩阵
	fout << "相机内参数矩阵：" << endl;
	fout << intrinsic_matrix << endl;
	fout << "畸变系数：\n";
	fout << distortion_coeffs << endl;

	File_Help.SaveCameraParams(calibration_file_path, intrinsic_matrix, distortion_coeffs);

	for (int i = 0; i < image_Seq.size(); i++)
	{
		fout << "图 " << Img_Vec[i] << " 的旋转向量：" << endl;
		fout << rotation_vectors[i] << endl;

		//将旋转向量转换为相对应的旋转矩阵
		Rodrigues(rotation_vectors[i], rotation_matrix);
		fout << "图 " << Img_Vec[i] << " 的旋转矩阵：" << endl;
		fout << rotation_matrix << endl;
		fout << "图 " << Img_Vec[i] << " 的平移向量：" << endl;
		fout << translation_vectors[i] << endl;

		File_Help.Save_RT_Params(".\\image\\source\\" + Img_Vec[i] + ".xml", rotation_matrix, translation_vectors[i]);
	}
	cout << "完成保存...." << endl;
	fout << endl;
	cout << "保存矫正图像....." << endl;
	for (int i = 0; i < image_Seq.size(); i++)
	{
		Mat Correted_Img = Api.Correct_Img(image_Seq[i], intrinsic_matrix, distortion_coeffs);
		imwrite(chess_boardCorner_path + Img_Vec[i] + "_d.bmp", Correted_Img);
	}
	cout << "保存结束....." << endl;
}

标定结果：

 标定结果影响因素：