实验目的

1. 掌握分治法思想。
2. 学会最近点对问题求解方法。

实验内容与结果

实验要求

1. 对于平面上给定的N个点，给出所有点对的最短距离，即，输入是平面上的N个点，输出是N点中具有最短距离的两点。

2. 要求随机生成N个点的平面坐标，应用蛮力法编程计算出所有点对的最短距离。

3. 要求随机生成N个点的平面坐标，应用分治法编程计算出所有点对的最短距离。

4. 分别对N=100000—1000000，统计算法运行时间，比较理论效率与实测效率的差异，同时对蛮力法和分治法的算法效率进行分析和比较。

5. 如果能将算法执行过程利用图形界面输出，可获加分。

分治法思想：将一个难以直接解决的大问题，分割成规模较小的相同问题。

具体的说：

1.将待求解的较大规模的问题分割为k个小规模的问题。

2.对这k个子问题分别求解。

3.如果子问题的规模仍然不够小，接着分割，直到问题规模小到可以直接求出解为止。

最近点对问题：对平面上给定的n个点，从所有点对中找出最短距离，即，输入是平面上的n个点，输出是n点中具有最短距离的两点。

1.暴力法

n个点存在n(n-1)/2个点对，逐一查阅各个点对，找出最小的值。

伪代码如下：

时间复杂度：
因为需要遍历n(n-1)/2种情况来找出最小值，最好、最坏、平均情况的时间复杂度都相同，为O(n) = T(n(n-1)/2) = O(n2)

空间复杂度：
因为需要一个变量来存储最小值，所以空间复杂度为O(1)。

运行时间

可以看出，理论时间和实际时间基本吻合，实际时间略小于理论时间；随着数据量的增加，运行时间急剧上升。

2.分治法

1.  预处理：根据输入点集S中的x轴和y轴坐标进行排序，得到X和Y,很显然此时X和Y中的点就是S中的点。

2.  点数较少时的情形

当点数较少时，可以直接进行计算。

3.  点数|S|>3时，将平面点集S分割成为大小大致相等的两个子集SL和SR，选取一个垂直线L作为分割直线，如何以最快的方法尽可能均匀平分？注意这个操作如果达到θ(n^2)效率，将导致整个算法效率达到θ(n^2)。

当点数较多时，应采取分治法，将平面分割，此时存在三种情况：
[1] 最短点对p1，p2均在左侧。
[2] 最短点对p1在左侧，p2在右侧
[3] 最短点对p1，p2均在右侧。

4.  两个递归调用，分别求出SL和SR中的最短距离为dl和dr。
对于情况[1]和情况[3]，运用递归可以简便的解决，难点在于情况[2]。

5.  取d=min(dl, dr)，在直线L两边分别扩展d，得到边界区域Y，Y’是区域Y中的点按照y坐标值排序后得到的点集（为什么要排序？），Y'又可分为左右两个集合Y’L和Y’R

对于中间的部分，按y进行排序，方便后面进行点的比较。

6.  对于Y’L中的每一点，检查Y’R中的点与它的距离，更新所获得的最近距离，注意这个步骤的算法效率，请务必做到线性效率，并在实验报告中详细解释为什么能做到线性效率？

由中线左边和中线右边的点对距离不小于d可知，若有距离小于d的点对，一定是一个点在左边，一个点在右边。

并且，因为距离小于d，那这两点一定是在一个长宽分别为2d和d的矩形内，且分别位于两边的边长为d的正方形内。

由鸽笼定理知每个小正方形最多有4个点，那两个小正方形就有8个点，又因为有2个点重合，故只需要比较6个点。

换而言之，若比较排序好后的6个点还没找到比d小的距离值，那这个点一定不会是最近点对中的点，那么接下来取下一个点为基准点进行比较。

伪代码如下：

 
时间复杂度：
递归算法复杂度为2T(n/2)，递归前的排序算法时间复杂度为O(nlog n)，
总算法复杂度T(n) = 2T(n/2) + O(nlog n)，
由主定理法及该算法a=b=2，nlog n = f(n) > nlogb a = n，
则该算法时间复杂度T(n)=O(f(n)) = O(nlog n)。

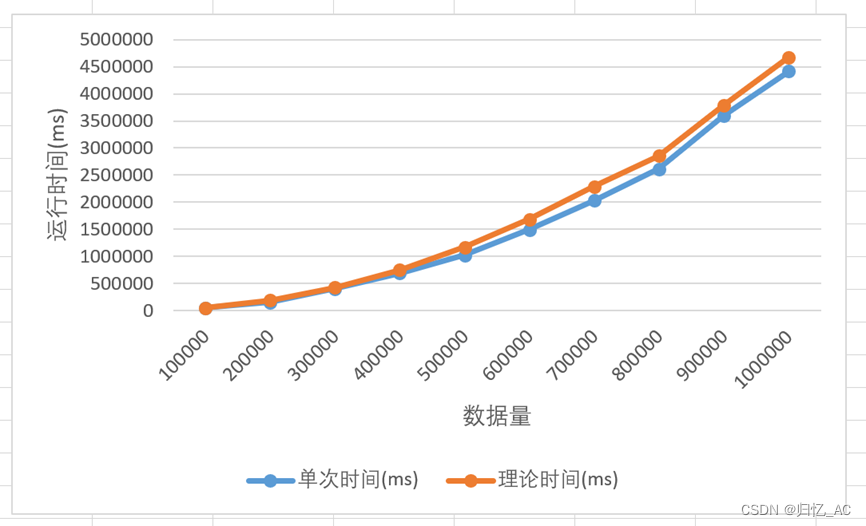
运行时间

 
可以看出，理论时间和实际时间基本一致，之所以会有细微的差别，是因为有一些代码耗时较小而在理论计算中被忽略。

可以明显的看出，分治法所用时间较少，运行速度较快。
 

实验总结

由实验数据和图像可知，在大数据量的处理过程中，分治法耗时远远小于暴力法，效率较高。因此，在处理大量数据时，应当选用分治法。

分治算法的核心思想就是将大的问题分割成小的问题来解决，以此达到提高运行效率的目的。

在本实验分治算法的合并中，很关键的一步就是判断出只需要最多比较6个点，极大地提高了算法效率，降低了运行时间。

实验伪代码

for i=0 to n-1			//i的范围0~n-1 
	for j=i to n-1		//j的范围i~n-1
		if(dist(d[i],d[j])<min)	//如果小于min则更新min 
			min=dist(d[i],d[j])
			
divide(l,r) //divide分治进行递归 
	if(l==r)//只有一个点时 
		return max
	if(l+1==r)//只有两个点时 
		retuen dist(d[l],d[r])
				
	mid=(l+r)/2	//分治递归 
	juli1=divide(l,mid)
	juli2=divide(mid+1,r)
	
	juli=min(juli1,juli2)//取小值 
	
	midd[]=d[mid.x+-juli]//取中间部分 
	sort(midd)			//排序 
	for i=0 to geshu-1  //比较 
		for j=i+1&&j<i+6
			if(dist(midd[i],midd[j])<juli)
				juli=dist(midd[i],midd[j])

 

实验代码 

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;

# define MAX 999999

int n;//点的个数，十万到一百万
double final;//最近点对距离

struct dian
{
	double x, y;
	dian() { x = y = -1; };
	dian(double xx, double yy)
	{
		x = xx; y = yy;
	}
}; 
dian* dians;//存储全部点集
dian* middians;//存储中间部分点集
dian d1, d2;//最终最近的两点

double dist(dian d1, dian d2)//求两点间距离
{
	return sqrt(pow(d1.x - d2.x, 2)+pow(d1.y - d2.y, 2));
}

bool cmpxy(dian a, dian b)//按先x后y排序
{
	if(a.x!=b.x)
		return a.x < b.x;
	return a.y < b.y;
}

bool cmpy(dian a, dian b)//按y排序
{
	return a.y < b.y;
}

void baoli()//暴力解法
{
	int i, j;
	for(i=0;i<n;i++)
		for (j = i + 1; j < n; j++)
		{
			double juli = dist(dians[i], dians[j]);
			if (juli < final)
			{
				final = juli;
				d1 = dians[i];
				d2 = dians[j];
			}
		}
}

double divide(int l, int r)//分治法
{
	double juli = MAX;

	if (l == r)//只有一个点时
		return juli;

	if (l + 1 == r)//只有两个点时
	{
		juli = dist(dians[l], dians[r]);
		if (juli < final)
		{
			juli = final;
			d1 = dians[l];
			d2 = dians[r];
		}
		
		//此处按y大小对二者进行排序 ，则之后就不需要按y大小sort中间部分 。将时间复杂度从O(nlog n)变为O(n) 
		if(dians[l].y>dians[r].y)
			swap(dians[l],dians[r]);
		return juli;
	}

	int mid = (l + r) / 2;//分治递归
	double juli1 = divide(l, mid);
	double juli2 = divide(mid + 1, r);

	juli = min(juli1, juli2);//取左右两部分中最小的和final比较，若小于final则更新final
	if (juli < final)
	{
		final = juli;
		if (juli == juli1)
		{
			d1 = dians[l];
			d2 = dians[mid];
		}
		else
		{
			d1 = dians[mid + 1];
			d2 = dians[r];
		}
	}

	int i, j, k=0;//k在循环中做标记，循环结束后为数组长度
	for (i = l; i < r; i++)//以mid为轴，将其左右长度各为dist的点存入数组middians中
	{
		if (fabs(dians[mid].x - dians[i].x) <= juli)
			middians[k++] = dians[i];
	}

	//sort(middians, middians + k, cmpy);//按y进行排序 见第74行 

	for(i=0;i<k;i++)
		for (j = i + 1; j<k&&j<i+6&&middians[j].y-middians[i].y<juli; j++)//由鸽笼原理知只需比较6个点，以此达到线性效率
		{
			double juli3 = dist(middians[i], middians[j]);
			if (juli3 < juli)
			{
				juli = juli3;
				if (juli < final)
				{
					final = juli;
					d1 = middians[i];
					d2 = middians[j];
				}
			}
		}
	return juli;
}

void show()
{
	cout << "最近的点对为以下两点" << endl;
	cout << "(" << d1.x << "," << d1.y << ")" << endl;
	cout << "(" << d2.x << "," << d2.y << ")" << endl;
	cout << "最近距离大小为" << final << endl;
}


int main()
{
	int i,k;
	for (k = 1; k <= 10; k++)//从十万到一百万
	{
		n = k*100000;
		cout << "点的个数n= " << n << endl;
		dians = new dian[n];//动态分配数组
		middians = new dian[n];

		srand(time(0));

		for (i = 0; i < n; i++)	//分配随机数
		{
			double y = rand() /	(double)RAND_MAX * n;
			double x = rand() / (double)RAND_MAX * n;
			dians[i]=dian(x, y);
		}

		sort(dians, dians + n, cmpxy);//按先x后y进行排序

		/*
		for (i = 0; i < n; i++)	//输出随机生成的点对
			cout << dians[i].x << " " << dians[i].y << endl;
		cout << endl;
		*/

		int qi, zhi;
		
		final = MAX;
		qi = clock();//记录运行时间
		baoli();
		zhi = clock();
		cout << "暴力法结果如下" << endl;
		show();
		cout << "耗时为" << zhi-qi << "ms" << endl << endl;
		

		final = MAX;
		qi = clock();
		divide(0, n - 1);
		zhi = clock();
		cout << "分治法结果如下" << endl;
		show();
		cout << "耗时为" << zhi-qi << "ms" << endl << endl;
	}
}

（by 归忆）