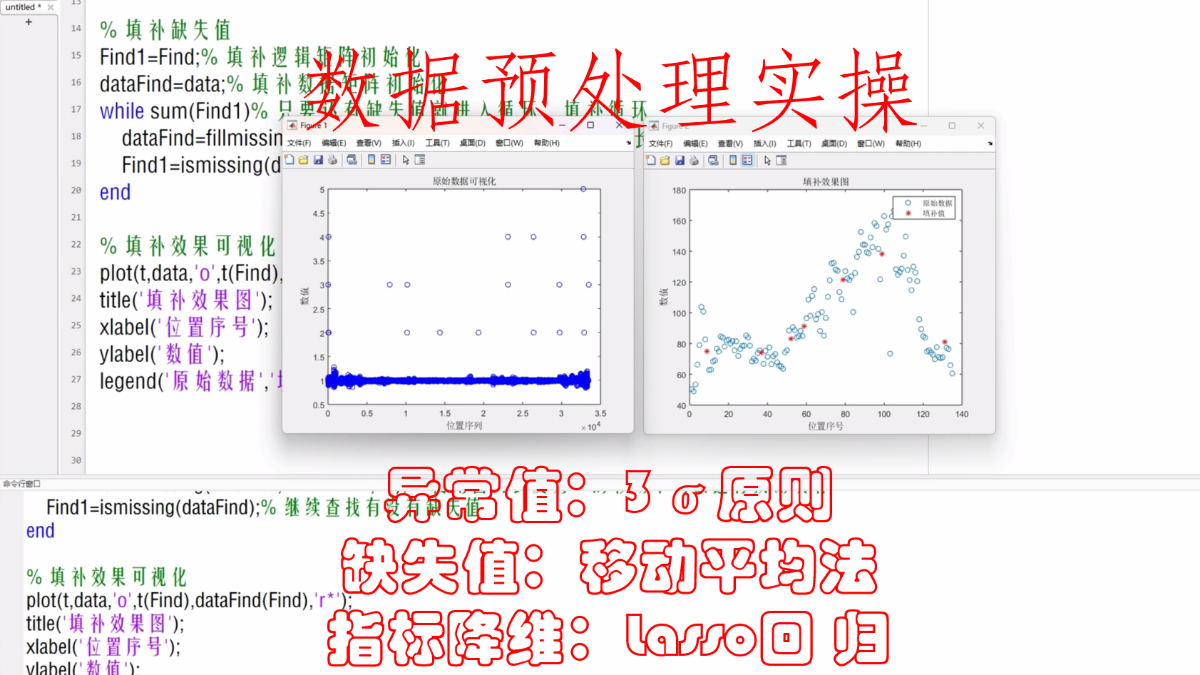
数模实操演示|数据预处理:异常值、缺失值、指标降维
本文将从异常值、缺失值、指标降维这三个方面分别进行实操演示。对于三个方面涉及的算法(方法)分别为:3σ原则、简单移动平均法、Lasso回归。所有的数据图片和代码在网盘可自行下载。链接:https://pan.baidu.com/s/1dio2TCMqgtZy3lyT7B6i7g?pwd=p5pu提取码:p5pu本文是作操作演示,不对原理进行解释。目录摘要一、3σ原则剔除异常值1、3σ原则方法简介2
摘要
无论是运筹优化还是数据挖掘,对数据进行预处理都是必不可少的一项进程。本文将从异常值、缺失值、指标降维这三个方面分别进行实操演示。对于三个方面涉及的算法(方法)分别为:3σ原则、简单移动平均法、Lasso回归。所有的数据图片和代码在网盘可自行下载。
链接:https://pan.baidu.com/s/1dio2TCMqgtZy3lyT7B6i7g?pwd=p5pu
提取码:p5pu
本文是作操作演示,不对原理进行解释。
目录
一、3σ原则剔除异常值
1、3σ原则方法简介
在统计学中,如果一个变量服从正态分布,且它的均值是,标准差是
,那么数据将服从如下分布:

因此在题目没有说明异常值类型的时候,使用3σ原则剔除离群点是一种较为简单且方便的方法。源码如下:
2、3σ剔除异常值MATLAB源码
clear;clc
data=xlsread("剔除数据演示.xlsx");
n=length(data);
t1=1:n;
figure(1)
plot(t1,data,'bo')
title('原始数据可视化举例');
xlabel('位置序列');
ylabel('数值');
ave=sum(data)/n% 平均值
std=std(data)% 标准差
p1=ave-3*std;% 上界
p2=ave+3*std;% 下界
index=[]% 索引矩阵
cnt=1;
for i=1:n
if data(i)<p1 | data(i)>p2% 3sigma原则
index(cnt)=i;
cnt=cnt+1;
end
end
m=length(index);
data(index(1:m),:)=[];% 离群点剔除
t2=1:length(data);
derta_num=n-length(data)
disp(['第一维度剔除异常值共:', num2str(derta_num) '个']);
figure(2);
plot(t2,data,'*')
title('剔除数据可视化举例');
xlabel('位置序列');
ylabel('数值');3、结果可视化
原始数据可视化如下:

剔除异常值后的数据可视化如下:

二、 简单移动平均法填补缺失值
1、简单移动平均法简介
移动平均法是用一组最近的实际数据值来预测未来一期或几期内数据的一种常用方法。移动平均法预测的期数不宜过多,因此选择来插值较为适合。当数据走向趋势较为平稳,且不存在季节性因素时,移动平均法能有效地消除预测中的随机波动,是非常有用的。移动平均法根据预测时使用的各元素的权重不同,可以分为:简单移动平均和加权移动平均。本文只使用简单移动平均法。
2、简单移动平均法填补数据源码
clear;clc
data=xlsread("填补数据演示.xlsx")% 加载数据
n=length(data);
disp(['共有数据:' num2str(n) '个']);
% 寻找缺失值
t=1:n;% 生成位置序号
Find=ismissing(data);% 查找缺失值,Find是逻辑矩阵,缺失值在Find中表示为1
plot(t,Find,'*')
title("缺失值位置");
xlabel("位置序号");
ylabel("是否为缺失值");
% data(Find) % 显示缺失值位置
disp(['缺失值个数为:' num2str(sum(Find))]);
% 填充缺失值
Find1 = Find;% 填补逻辑矩阵初始化
dataFind = data;% 填补数据矩阵初始化
while sum(Find1) % 如果还存在缺失值就继续插补
dataFind = fillmissing(dataFind,'movmean',30); % 使用窗口长度为 30 的移动均值法填充缺失数据。
Find1=ismissing(dataFind);% 更新逻辑矩阵
end
% 填补效果可视化
plot(t,data,'o',t(Find),dataFind(Find),'rx')
title('填补效果图')
xlabel('位置序号');
ylabel('数值');
legend('原始数据','填补值')
3、结果可视化
填补效果图如下:

三、Lasso回归对指标进行降维
1、Lasso回归简介
Lasso回归是一种收缩估计方法,其基本思想是在回归系数的绝对值之和小于一个常数的约束条件下,使残差平方和最小化,从而能够产生某些严格等于0的回归系数,进一步得到可以解释的模型。由于数据中往往有多个指标,为减少问题的复杂性以及避免出现完全多重共线性,对指标降维是一项非常重要的步骤。
2、Lasso演示
本文给出的诸多指标不需要搞清楚,你只需要知道成交量股这个指标是因变量,我们从剩下的指标中去提取关键指标即可。Lasso回归需要使用Stata软件进行操作。这里的lopt命令是为了找到一个使得均方误差最小,seed是随机种子数,可自行设定,目的是使结果具有可重复性,默认k等于10,即10折交叉验证。
输入命令:
cvlasso 成交量股 前收盘价 开盘价 最高价 最低价 收盘价 成交金额元 涨跌 涨跌幅,lopt seed(500)
结果如下图所示:

即可将前收盘价、最高价和成交金额作为关键指标。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)