基于MATLAB的MIMO预编码设计：优化迫零算法（附完整代码与分析）

图中“RFChain” 全称为RadioFrequencyChain，代表射频链路。此MIMO预编码包含了基带预编码W（改变幅度和相位）和射频预编码F（改变相位）。用户k端收到的信号为：上式中代表基站到用户的信道矩阵，F代表射频预编码，W代表基带预编码，s代表发射信号向量，代表加性高斯白噪声。发射流的最大数量为K，则：用户k端受到的信干噪比（SINR）为：上式子中P代表基站的发射功率。其他参数的意

唠嗑！

6089人浏览 · 2023-02-24 22:04:02

唠嗑！ · 2023-02-24 22:04:02 发布

一.介绍

二. 对比本方案优化后的迫零算法与原始的迫零算法

一.介绍

图中“RF Chain” 全称为Radio Frequency Chain，代表射频链路。

此MIMO预编码包含了基带预编码W（改变幅度和相位）和射频预编码F（改变相位）。用户k端收到的信号为：

上式中 $h^H_k$ 代表基站到用户的信道矩阵，F代表射频预编码，W代表基带预编码，s代表发射信号向量， $n_k$ 代表加性高斯白噪声。

发射流的最大数量为K，则：

$||FW||^2_F=K$

用户k端受到的信干噪比（SINR）为：

上式子中P代表基站的发射功率。其他参数的意义上面已解释。

系统的总频谱效率为：

上式中E[]代表求数学期望。其他参数的意义上面已解释。

依据基础的迫零算法进行改进，将K个射频链路输出与 $N_t$ 个发射天线进行耦合，仅仅进行相位控制，然后在基带上进行低维多流处理，最终降低用户间的干扰，本方案创新性提出相位-迫零算法（Phased-ZF)，优点：

•极大降低计算复杂度；

•性能逼近原始ZF（迫零）算法；

对该预编码的两步，总结来看为如下：

二. 对比本方案优化后的迫零算法与原始的迫零算法

三. 源代码

一共八个文件，两个主运行文件，六个函数文件。注意最后的两个文件为实际产生图像的代码部分。

（1）

%  BD precoder design subfunction r = CalBDPrecoder(G, K) --%
%  Input:  H, K*Nr x Nt,  aggregate channel, 
%          NsUE, # streams per user, K x 1
%  Output: r, Nt x K*Lr BD precoder

function r = CalBDPrecoder(H, NsUE) % no waterfilling
if nargin <= 1
    NsUE = ones(size(H,1)); % essentially ZF precoding with column normalization
end
[NR, Nt] = size(H);
K = length(NsUE);
Nr = NR/K;
F = [];% BD precoder initialization

%***** Standard BD design based on paper "ZF methods for DL spatial multiplexing..." ***%
for iK = 1 : K
    Gj = H(((iK-1)*Nr+1):(iK*Nr),:);
    G_tilde = H;
    G_tilde(((iK-1)*Nr+1):(iK*Nr),:) = []; % Delete iK-user's channel, G_tilde
    [U, S, V] = svd(G_tilde);
    rv = rank(G_tilde);
    
    Htmp = Gj*V(:, (rv + 1):Nt );
    Lr = rank(Htmp);% # of data streams accommodated by iK user
    [Ut, St, Vt] = svd(Htmp);
    Ftmp = V( : , (rv + 1):Nt)*Vt(: , 1:NsUE(iK));
    F = [F Ftmp];
end
r = F;

（2）

% Function to calculate achievable rates
% r = CalRate(H, W, K);
% Input: H, channel instantialization, (KNr) x Nt
%        W, precoding matrix, column normalized, Nt x Ns
%        NsUE, a vector showing # streams of each UE, K x 1
%        Incov, input covariance, i.e., power allocation, Ns x Ns
% Output: r, achievable rate

function r = CalRate(Incov, H, W, NsUE)
Incov = diag(Incov); % vectorize
if nargin <= 3 
    NsUE = ones(size(W,2), 1);% set default, single stream per user
end

K = length(NsUE);% # of users
Nr = size(H, 1)/K;% # antenna per user, assuming equal
Ns = sum(NsUE);% total # data streams

rate = 0;
for iK = 1 : K
        
    st = sum(NsUE(1:(iK-1)))+1;
    ed = sum(NsUE(1:iK));
    
    Hj = H( (Nr*(iK-1)+1) : (Nr*iK), :);% user channel of i
    Wj = W(:, st:ed);% precoder for user i
    covj = diag(Incov(st:ed));
    Pj = Hj*Wj*covj*(Hj*Wj)'; % signal power term
    
    Wintf = W;% precoder for interferers
    covtp = Incov;
    
    Wintf(:, st:ed) = [];
    covtp(st:ed) = [];
    cov_intf = diag(covtp);
    Pintf = (Hj*Wintf)*cov_intf*(Hj*Wintf)';% interference power term
    
    rate = rate + log2(det( eye(Nr) + inv( eye(Nr) + Pintf ) * Pj ));
end

r = rate;

（3）

% expintn exponential intergral of the order n
% r = expintn(x, n) gives integral from 1 to inf of (exp(-xt)/t^n)dt, for x > 0

function r = expintn_noMaple(x, n)

if n >= 2
    sum = 0;
    for m = 0 : (n-2)
        sum = sum + (-1)^m*factorial(m)/x^(m+1);
    end

    minuend = x^(n-1) * (-1)^(n+1)/factorial(n-1) * expint(x);
    subtractor = x^(n-1) * (-1)^(n+1)/factorial(n-1) * exp(-x) * sum;
    r = minuend - subtractor;
else
    r = expint(x);
end

（4）

% expintn(x, n) is an an exponential integral of order n with input x,
% computed using maple

function r = expintn(x, n)

cmd_str = sprintf('evalf[16](Ei(%d, %g));', n, x);
r = double(maple(cmd_str));

（5）

% Generate a simplified MU-MIMO channel based on uniform linear array (ULA)
% "The capacity optimality of beam steering in large mmWave MIMO channels"
% [H, Gain, At] = GenChannelSimp (Nt, K, Ncls)
% Input: Nt, number of TX antennas
%        K, number of single-antenna UEs
%        Ncls, number of clusters, single path per cluster
%        d, normalized antenna spacing
% Output: H, generated MU-MIMO channel
%         Gain, complex gain of each path
%         At, concatenation of array response vectors

function [H, Gain, At] = GenChannelSimp(Nt, K, Ncls, d)
if nargin <= 3
    d = 1/2;
end

% spread = pi/12;% [-15, 15]
spread = pi;
ang = (2*rand(Ncls, K)-1)*spread; % generated path angles, uniform distribution
Gain = (randn(Ncls, K) + j*randn(Ncls, K))/sqrt(2);

At = zeros(Nt, Ncls, K);
H = zeros(K, Nt);
for ik = 1 : K
    tmp = 0 : (Nt-1);
    tmp = tmp(:);
    kron1 = j*2*pi*d*tmp;
    kron2 = sin(ang(:, ik));
    kron2 = kron2.';
    kronr = kron(kron1, kron2);
    
    At(:, :, ik) = 1/sqrt(Nt) * exp(kronr);
    H(ik, :) = sqrt(Nt/Ncls) * Gain(:, ik).' * At(:, :, ik)';
end

（6）

% Quant(B, W) quantizes phases of each element in W up to B bits of precision

function r = Quant(B, W)
delta = 2*pi/2^B; % quantization interval
r = zeros(size(W, 1), size(W, 2));% ininitialize quantized matrix

for i1 = 1 : size(W, 1)
    for i2 = 1 : size(W, 2)
        ph = phase(W(i1, i2)); % ph in [-pi, pi]
        phq = floor(ph/delta)*delta +(mod(ph, delta) > delta/2)*delta ;% quantized phase
        r(i1, i2) = exp(j*phq);
    end
end
r = 1/sqrt(size(W, 1)) * r;
end

（7）

%   Massive MU-MIMO under chain limitations, single-antenna UE
%   Hybrid precoding with ZF at baseband and phase reversal at analog
%   Compare full-complexity ZF (FC-ZF) vs Hybrid

tic; clear; clc

Nt = 8;
K = 2; % UE number
B1 = 1; % quantized analog beamforming, up to B bits of precision
B2 = 2;

SNR = 0 : 5 : 30; 
nSNR = length(SNR);
channNum = 1e3;

rateZF = zeros(nSNR, 1); % FC-ZF
rateZFA = zeros(nSNR, 1);
rateHyb = zeros(nSNR, 1);% W = ZF at baseband, F = PR at analog
rateHybA = zeros(nSNR, 1);
rateQHyb1 = zeros(nSNR, 1);% Quantized PR, ZF at baseband
rateQhyb2 = zeros(nSNR, 1);

for isnr = 1 : nSNR
    
    P = 10^(SNR(isnr)/10);
    
    % ====================================================================
    % ===================== Analytical result ============================
    % ====================================================================
    % ==========  ZF analytical results =============
    s = 0;
    for k = 1 : (Nt)
        rho = P/K;
        s = s + exp(1/rho)*log2(exp(1)) * expintn_noMaple(1/rho, k); % use maple for expintn()
        % s = s + exp(1/rho)*log2(exp(1)) * expintn_noMaple(1/rho, k); % if no maple installed
    end    
    rateZFA(isnr) = K*s;
    
    % ========= Hybrid precoding analytical results  ==========
    rateHybA(isnr) = K*log2(1 + (pi/4) * (P*Nt)/K );
    
    % ====================================================================
    % ===================== Simulation result ============================
    % ====================================================================   
    for ichannel = 1 : channNum
        
        H = (randn(K, Nt) + j*randn(K, Nt))/sqrt(2);
        
        %   =============  ZF preocidng, numerical  ================ 
        WtZF = H'*inv(H*H');
        WZF = WtZF*inv(sqrt(diag(diag(WtZF'*WtZF)))); % normalized columns
        rateZF(isnr) = rateZF(isnr) + CalRate(P/K*eye(K), H, WZF);
        
        %   ============ Hybrid, numerical ===============
        F = 1/sqrt(Nt)*exp(j.*angle(H))';
        Fb = CalBDPrecoder(H*F);% baseband, same as inverse with column normalization
        wt = F*Fb;% aggregate precoder
        WPR = wt*inv(sqrt(diag(diag(wt'*wt))));   
        rateHyb(isnr) = rateHyb(isnr) + CalRate((P/K)*eye(K), H, WPR);% ZF-PRP
        
        %   ============= Quantized ZF-PR precoding ============
        FQPR1 = Quant(B1, F);% analog RF
        wt = FQPR1*CalBDPrecoder(H*FQPR1);
        WQPR1 = wt*inv(sqrt(diag(diag(wt'*wt))));
        rateQHyb1(isnr) = rateQHyb1(isnr) + CalRate((P/K)*eye(K), H, WQPR1);
        
        WtQPR2 = Quant(B2, F);
        wt = WtQPR2*CalBDPrecoder(H*WtQPR2);
        WQPR2 = wt*inv(sqrt(diag(diag(wt'*wt))));
        rateQhyb2(isnr) = rateQhyb2(isnr) + CalRate((P/K)*eye(K), H, WQPR2);      
    end
    isnr   
end

rateZF = rateZF/channNum;
rateHyb = rateHyb/channNum;
rateQHyb1 = rateQHyb1/channNum;
rateQhyb2 = rateQhyb2/channNum;

LineWidth = 1.5;
MarkerSize = 6;
figure
plot(SNR, abs(rateZF), 'k-x', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold on
plot(SNR, abs(rateZFA), 'bo', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize);
hold on
plot(SNR, abs(rateHyb),'r-*', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold on
plot(SNR, abs(rateHybA), 'gd', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold on
plot(SNR, abs(rateQHyb1), 'b-^', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold on
plot(SNR, abs(rateQhyb2), 'b-v', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold off
legend('FC-ZF, simulation', 'FC-ZF, analytical', ...
    'PZF, simulation', 'PZF, analytical', ...
    'Quantized PZF, B = 1','Quantized PZF, B = 2');
xlabel('SNR (dB)')
ylabel('Spectral Efficiency (bps/Hz)')
title(sprintf('Nt = %d, K = %d', Nt, K))
grid
% saveas(gcf, sprintf('MassiveCompareScheme-Nt%d-K%d', Nt, K)); 
% saveas(gcf, sprintf('MassiveCompareScheme-Nt%d-K%d-PhaseOfZf', Nt, K));

toc

（8）

% DESCRIPTION
%   mmWave massive MU-MIMO under chain limitations, single-antenna UE
%   Hybrid precoding with ZF at baseband and Phase Reversal (PR) Preocidng at analog
%   Compare full-complexity ZF (FC-ZF), Hybrid, QHybrid, and B-MIMO numerically

tic; clear all; clc

Nt = 128;
K = 4; % UE number
Np = 10; % number of paths per user
B1 = 1; % quantized analog beamforming, up to B bits of precision
B2 = 2;

SNR = -30 : 5 : 0; 
nSNR = length(SNR);
channNum = 1e3;

rateZF = zeros(nSNR, 1); % FC-ZF
rateHyb = zeros(nSNR, 1);% W = ZF at baseband, F = PR at analog
rateHybQ1 = zeros(nSNR, 1);% Quantized hybrid precoding
rateHybQ2 = zeros(nSNR, 1);
rateBMIMO = zeros(nSNR, 1);% Multiuser beamspace MIMO precoder (BMIMO)

for isnr = 1 : nSNR
    
    P = 10^(SNR(isnr)/10);
    
    for ichannel = 1 : channNum
        
        [H, Gain, At] = GenChannelSimp(Nt, K, Np, 0.5); % mmWave channel
        % H = K x Nt, Gain = Np x K, At = Nt x Np x K
        
        %   =============  ZF preocidng, numerical  ================ 
        WtZF = H'*inv(H*H');
        WZF = WtZF*inv(sqrt(diag(diag(WtZF'*WtZF)))); % normalized columns
        rateZF(isnr) = rateZF(isnr) + CalRate(P/K*eye(K), H, WZF);
        
        %   ============ Hybrid precoding, numerical ===============
        for ik = 1 : K
            ph = - phase(H(ik,:));
            ph = ph(:);
            F(:,ik) =1/sqrt(Nt)* exp(j.*ph); % analog RF preprocessing
        end
        Fb = CalBDPrecoder(H*F);% digital baseband, same as inverse with column normalization
        wt = F*Fb;% aggregated precoder
        WPR = wt*inv(sqrt(diag(diag(wt'*wt))));   
        rateHyb(isnr) = rateHyb(isnr) + CalRate((P/K)*eye(K), H, WPR);% ZF-PRP
        
        %   ============= Quantized hybrid precoding ============
        FQPR1 = 1/sqrt(Nt) * Quant(B1, F);% analog RF
        wt = FQPR1*CalBDPrecoder(H*FQPR1);
        WQPR1 = wt*inv(sqrt(diag(diag(wt'*wt))));
        rateHybQ1(isnr) = rateHybQ1(isnr) + CalRate((P/K)*eye(K), H, WQPR1);
        
        WtQPR2 = 1/sqrt(Nt) * Quant(B2, F);
        wt = WtQPR2*CalBDPrecoder(H*WtQPR2);
        WQPR2 = wt*inv(sqrt(diag(diag(wt'*wt))));
        rateHybQ2(isnr) = rateHybQ2(isnr) + CalRate((P/K)*eye(K), H, WQPR2);

        % =========== Multiuser Beamspace MIMO precoder (B-MIMO) ============== %
        D = dftmtx(Nt);
        Hf = H*D;
        [maxVal, maxInd] = sort(diag(Hf'*Hf), 'descend'); % sort column with decreasing magnitude
        FBMIMO = D(:, maxInd(1:K));
        FbBMIMO = pinv(H*FBMIMO);
        Wt = FBMIMO*FbBMIMO;% analog x baseband precoding
        WBMIMO = Wt*inv(sqrt(diag(diag(Wt'*Wt))));
        rateBMIMO(isnr) = rateBMIMO(isnr) + CalRate((P/K)*eye(K), H, WBMIMO);
    end
    isnr   
end

rateZF = rateZF/channNum;
rateHyb = rateHyb/channNum;
rateHybQ1 = rateHybQ1/channNum;
rateHybQ2 = rateHybQ2/channNum;
rateBMIMO = rateBMIMO/channNum;

LineWidth = 1.5;
MarkerSize = 6;
figure
plot(SNR, abs(rateZF), 'k-o', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold on
plot(SNR, abs(rateHyb),'r-*', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold on
plot(SNR, abs(rateHybQ1), 'b-^', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold on
plot(SNR, abs(rateHybQ2), 'b-v', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold on
plot(SNR, abs(rateBMIMO), 'm-s', 'LineWidth', LineWidth, 'MarkerSize', MarkerSize)
hold off
legend('FC-ZF Precoding', 'Hybrid Precoding', 'Quantized Hybrid Precoding, B = 1',...
    'Quantized Hybrid Precoding, B = 2', 'B-MIMO Preocoding');
xlabel('SNR (dB)')
ylabel('Spectral Efficiency (bps/Hz)')
% title(sprintf('Nt = %d, K = %d,  Np = %d',Nt, K, Np))
grid

saveas(gcf, sprintf('MainCompareScheme-Nt%d-K%d-Np%d', Nt, K, Np)); % save current figure to file
toc

四. 运行结果及分析

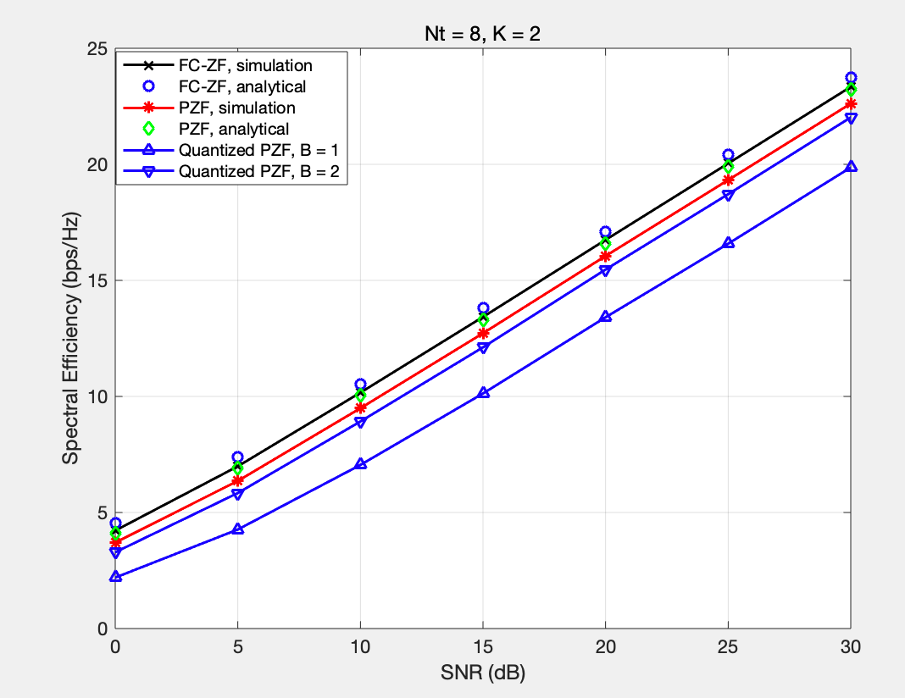
4.1 天线数为8

ZF: Zero Forcing 迫零算法 SNR： Signal Noise Ratio 信噪 PZF：Phased-Zero Forcing

对比三种算法性能：原始ZF算法，PZF算法，量化后的PZF算法。

横向对比：三种算法均满足，随着SNB从0增加到30dB，频谱效率从2.166增大到23.75 bps/HZ，符合正常逻辑；

纵向对比：在同一SNR下，性能从最优到最劣，理论ZF值、实际ZF仿真值、理论PZF值、实际PZF仿真值、精度到两位比特的PZF值、精度到1位比特的PZF值；

方案对比：本方案PZF比原始ZF性能略差（相差约0.7bps/Hz），但计算复杂性低得多，更具有实用价值；

量化对比：在PZF方案基础上，进一步约算，取近似比特可进一步形成Quantized PZF. 随着近似比特精度取值从1到2，频谱效率也会增大（约2.07bps/Hz）。性能降低但计算复杂度会更一步降低，增加应用价值；

4.2 天线数为128

图中B-MIMO 全称为Beamspace MIMO 代表的意义是波束空间MIMO

天线数 $N_t$ 为128:

横向对比：当SNR从-30增加到0dB，频谱效率整体上从0增加到19.63bps/Hz;

纵向对比：从最优到最劣：原始ZF预编码、本论文的混合预编码、比特近似精度取2的混合预编码、比特精度取1的混合预编码、波束空间MIMO方案；

以牺牲不足1bps/Hz的频谱效率，却能极大降低计算复杂度，降低MIMO对射频硬件的要求；

MATLAB代码运行时间：天线数为4时运行3秒左右，天线数为128时运行50.199667秒；

在信噪比为0dB时，本方案PZF频谱效率为18.35bps/Hz。设定4G基站采用4根天线，平均频谱效率为2.9 bps/Hz。设定5G基站天线数为64，平均频谱效率为10 bps/Hz【数据来源《物联网智库》】。

开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

“小满”安全车控操作系统正式在AtomGit开源

10月24日，由中国汽车工业协会指导，普华基础软件股份有限公司主办的“小满”安全车控操作系统开源发布会暨共建计划说明会成功举行。普华基础软件宣布将安全车控操作系统“小满”（简称“小满”）V24.10源代码正式在开放原子开源基金会（简称“基金会”）旗下AtomGit开源协作平台开源，并在AtomGit平