一、基本概念

• 1.人工智能研究的主要问题

    知识的获取，知识的表示，知识的运用
  

• 2.请简述知识、数据、信息之间的联系和区别

  数据、信息和知识是知识工作者对客观事物感知和认识的3个连贯的阶段。
  数据即事实，信息是事实的载体，知识是人对信息的加工、吸收、提取、评价的结果
  

• 3.盲目搜索和启发式搜索的异同点

  	描述
  盲目搜索	无需信息即可搜索	按预定的控制策略进行搜索，在搜索过程中获得的中间信息并不改变控制策略
  启发式搜索	信息搜索	在搜索中加入了与问题有关的启发性信息，用于指导搜索朝着最有希望的方向前进

• 4.简要解释回归、分类和聚类概念

  首先，根据训练数据是否有标记信息，将学习任务分为“监督学习”和“无监督学习”。其中分类和回归是前者的代表，聚类是后者的代表。
  其次，三者都是针对预测问题。如果预测的值是离散的，称为“分类”，如果是连续的，称为“回归”，如果事先没有标记信息（或者说训练集没有标准答案），那么就称为“聚类”。

  回归方法是一种对数值型连续随机变量进行预测和建模的监督学习算法。使用案例一般包括房价预测、股票走势或测试成绩等连续变化的案例。回归任务的特点是标注的数据集具有数值型的目标变量。也就是说，每一个观察样本都有一个数值型的标注真值以监督算法。

  分类方法是一种对离散型随机变量建模或预测的监督学习算法。使用案例包括邮件过滤、金融欺诈和预测雇员异动等输出为类别的任务。许多回归算法都有与其相对应的分类算法，分类算法通常适用于预测一个类别（或类别的概率）而不是连续的数值。

  聚类是一种无监督学习任务，该算法基于数据的内部结构寻找观察样本的自然族群（即集群）。使用案例包括细分客户、新闻聚类、文章推荐等。因为聚类是一种无监督学习（即数据没有标注），并且通常使用数据可视化评价结果。如果存在「正确的回答」（即在训练集中存在预标注的集群），那么分类算法可能更加合适。

• 5.简要回答个体、群体、染色体、基因、适应性这些生物遗传概念分别对应遗传算法中的哪些应用？

  生物遗传概念	遗传算法中的应用
  个体	解
  群体	根据适应度值选定的一组解（解的个数为群体的规模）
  染色体	解的编码（字符串，向量等）
  婚配	交叉选择两个染色体进行交叉产生一组新的染色体
  基因	解的编码中每一分量
  变异	编码的某一分量发生变化的过程
  适应性	适应度函数值
  适者生存	目标值比较大的解被选择的可能性大

• 6.知识的谓词表示

  • 1 有人喜欢打篮球，有人喜欢跑步，有人既喜欢打篮球也喜欢跑步

    P(x)：x是人
    L(x,y)：x喜欢y； 其中，y的个体域是{打篮球，跑步}。
    将知识用谓词表示为
    （∃x）(P(x)→L(x,打篮球)∨L(x,跑步)∨(L(x,打篮球)∧L(x,跑步)))

  • 2 新型计算机速度又快， 存储容量又大；
    解：定义谓词
    NC(x)：x是新型计算机
    F(x)：x速度快
    B(x)：x容量大
    将知识用谓词表示为(∀ x)(NC(x)→F(x)∧B(x))

  • 有人每天下午都去打篮球；
    解：定义谓词
    P(x)：x是人
    B(x)：x打篮球
    A(y)：y是下午
    将知识用谓词表示为：
    (∃x)(∀y)(A(y)→B(x)∧P(x))

  • 凡是喜欢编程序的人都喜欢计算机；
    解：定义谓词
    P(x)：x是人
    L(x,y)：x喜欢y
    将知识用谓词表示为：
    (∀x)(P(x)∧L(x, pragramming)→L(x,computer))

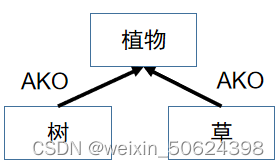
• 7. 语义网络表示
     AKO（A-Kind-Of）表示某个事物是另一个事物的一种类型
     AMO（A-Member-Of）表示某个事物是另一个事物的成员
     ISA（Is-A）表示某个事物是另一个事物的实例
     但不局限于这几个关系

  • 1 树和草都是植物
    

  • 2 树和草都有叶和根
    

  • 3 中国乒乓球队4:0战胜日本队
    

  • 4 高老师从7月到8月给计算机系学生讲《计算机网络》 课
    

• 8. 框架表示
  • 1 某人的基本情况，比如：包括姓名，年龄，身高，工作等等
    例如：
    框架名：〈教师-1〉
    姓名：夏冰年龄：36
    性别：女
    职称：副教授
    部门：计算机系软件教研室住址：〈adr-1〉
    工资：〈sal-1〉
    开始工作时间：1988，9
    截止时间：1996，7
  • 2 假设有以下一段天气预报： “北京地区今天白天晴， 偏北风3级， 最高气温12℃， 最低气温-2℃，体感温度5℃， 降水概率15%。 ”
    解：
    框架名：<天气预报>
    地域：北京
    时段：今天白天
    天气：晴
    风向：偏北
    风力：3级
    气温：最高：12℃
    最低：-2℃
    体感：5℃
    降水概率：15%

• 9.产生式推理，会根据规则库里面的规则推理给定事实所表示的动物，写出推理过程。比如：
  

  推理过程：

  第一步：检查规则库 IF 有奶 THEN 哺乳动物，其前件可以与事实库中的r16有奶匹配，执行该产生式，产生“哺乳动物”的新事实； 向事实库中添加 r21：哺乳动物；

  第二步：再次检查规则库 r7: IF 哺乳动物 AND 有蹄 THEN 有蹄类动物动物； 向事实库中添加 r22：有蹄类动物动物；

  第三步：再次检测规则库 r11: IF 有蹄类动物动物 AND 长脖子 AND 长腿 AND 暗斑点 THEN 长颈鹿；

  至此，得到明确分类结论，推理结束；

  事实库：

  r16：有奶
  r17：有蹄
  r18：长脖子
  r19：长腿
  r20：暗斑点
  r21：哺乳动物
  r22：有蹄类动物动物
  r23：长颈鹿

二、计算

• 1 计算向量X = (1, 1, 0, 1), Y = (1, 1, 1, 0)的余弦相似度，欧几里德距离，曼哈顿距离？
  余弦相似度：
  =(1+1+0+0)/(√3*√3)=2/3
  欧几里得距离公式：=√2
  曼哈顿距离公式：=2

• 2 搜索

  • 请使用深度优先搜索方法和宽度优先搜索方法找到从节点S到节点R的一条解路径（注意，不是搜索路径，例如，S->O->P->R就是一条解路径）。假设初始时OPEN = {1}， CLOSE = {}，给出访问每个节点时OPEN表和CLOSE表的变化。
    
    解：深度优先搜索：
    
    找到一条解路径：S => D => L => R
    这条路径不是最优解路径，最优解路径是S=>O=>R
    
  • 2
    
    解：
    
    不扩展的，{8,5,3},8达到深度限制，不能再扩展，关闭；5只有到8的路径，也不再扩展，关闭；3继续扩展。

• 3 用启发式搜索算法求解“八数码问题”，寻找从初始状态到目标状态的解路径，并给出每个状态的估价函数值。初始状态为S0，目标状态为Sg。
  

  解：
  

三、设计题

• 具有3个属性{A,B,C}和两个类别{C1,C2}的数据集，请利用朴素贝叶斯分类的方法预测记录（A=1,B=0,C=1）的类别标签，请给出具体的计算过程。
  
  理解朴素贝叶斯
  解：根据表中所给出的信息，可以得到属于类别C1和C2的概率分别为：
  P(Y=C1)=6/10, P(Y=C2)=4/10,
  同时，可以得到条件概率：
  P(A=0|Y=C1)=3/6, P(A=1|Y=C1)=3/6, P(A=0|Y=C2)=0, P(A=1|Y=C2)=1
  P(B=0|Y=C1)=4/6, P(B=1|Y=C1)=2/6, P(B=0|Y=C2)=2/4, P(B=1|Y=C2)=2/4
  P(C=0|Y=C1)=2/6, P(C=1|Y=C1)=4/6, P(C=0|Y=C2)=3/4, P(C=1|Y=C2)=1/4
  那么，
  记录（A=1,B=0,C=1）属于类别C1的概率为：
  P(A=1,B=0,C=1) = P(Y=C1)·P(A=1|Y=C1)·P(B=0|Y=C1)·P(C=1|Y=C1)
  = 6/10×3/6×4/6×4/6=2/15
  属于类别C2的概率为：
  P(A=1,B=0,C=1) = P(Y=C2)·P(A=1|Y=C2)·P(B=0|Y=C2)·P(C=1|Y=C2)
  = 4/10×1×2/4×1/4=1/20

  2/15>1/20，故属于类别C1