目录

 前言

设计思路

一、课题背景与意义

二、算法理论原理

2.1 注意力机制

2.2 模型优化算法

三、检测的实现

最后

---

 前言

       📅大四是整个大学期间最忙碌的时光,一边要忙着备考或实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。

        🚀对毕设有任何疑问都可以问学长哦!

         选题指导:

        最新最全计算机专业毕设选题精选推荐汇总

        大家好,这里是海浪学长毕设专题,本次分享的课题是

        🎯基于深度学习的天气状况预测系统 

设计思路

一、课题背景与意义

       天气状况对人们的日常生活、农业、交通运输、能源供应等方面都有着重要影响。准确预测天气状况对于提前采取相应的措施、合理安排活动、做好资源调配等具有重要意义。传统的天气预报方法主要基于数值模型和统计方法，但这些方法在处理复杂的天气现象和变化模式时存在一定的局限性。而深度学习作为一种强大的机器学习方法，具有自动学习特征和处理大规模数据的能力，被广泛应用于各个领域，包括天气预测。

二、算法理论原理

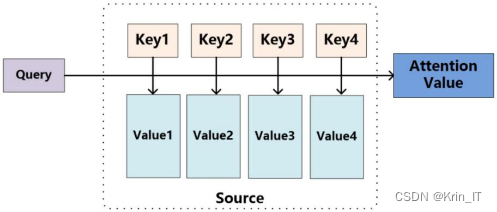
2.1 注意力机制

       提升 LSTM 模型性能的利器：注意力机制在保留中间输出的同时，有选择性地学习输入信号，并与输出信号关联。虽然引入注意力机制会增加计算量，但能显著提高模型性能。此外，注意力机制还能更好地理解输入顺序对结果的影响，深入探究模型的内在工作机理，并帮助排除特定输入-输出的故障。

       软注意力机制和硬注意力机制是两种不同的注意力机制，主要区别在于是否可微分。软注意力机制考虑了所有对象的全部特征，并对它们进行加权计算，权重范围在[0, 1]之间。它不会舍弃任何信息，即使某些信息对输出影响较小。相反，硬注意力机制的权重为0或1，只关注对输出有价值的对象，舍弃其他不重要的信息。

       软注意力机制通过神经网络模型提取特征向量，并使用加权求和计算加权特征向量。该过程是平滑且可微的，其中softmax层用于计算权重。此外，软注意力机制还根据上一时刻的隐藏信息决定下一时刻的注意力机制，对下一时刻编码器输出的隐藏信息进行调整。

2.2 模型优化算法

       为了优化模型，提高训练效率和预测精度，并充分发挥长短时记忆网络模型的优势，可以采用以下步骤：

• 网格搜索（Grid Search）与交叉验证（Cross Validation）结合：通过网格搜索尝试不同的超参数组合，如学习率、隐藏层大小等，以找到最佳的模型超参数组合。交叉验证用于评估每个超参数组合的性能，通过将训练数据划分为多个子集进行训练和验证，以准确评估模型的性能并避免过拟合。
• Adam优化算法：使用Adam优化算法来确定模型的最优权重和偏置。Adam是一种自适应学习率优化算法，结合了动量法和自适应学习率的优点。它能够根据每个参数的历史梯度和动量来调整学习率，从而更有效地更新模型参数。

       Adam算法是一种优化算法，用于调整模型中权重和偏置的更新值。它利用梯度的一阶矩估计和二阶矩估计来动态调整每个参数的学习率。Adam算法的流程如下：

• 计算梯度的一阶矩估计和二阶矩估计。
• 修正一阶矩估计和二阶矩估计的偏差。
• 根据修正后的一阶矩和二阶矩计算权重和偏置的修正量。
• 根据步长（学习率）和修正量更新模型的权重和偏置。

       通过使用Adam算法，可以自适应地调整学习率，从而更有效地更新模型的参数。它结合了动量法和自适应学习率的优点，能够在训练过程中平衡速度和稳定性，提高模型的训练效率和预测精度。

相关代码示例：

# 初始化参数
m = 0  # 一阶矩估计的初始值
v = 0  # 二阶矩估计的初始值
beta1 = 0.9  # 一阶矩估计的指数衰减率
beta2 = 0.999  # 二阶矩估计的指数衰减率
epsilon = 1e-8  # 用于数值稳定性的小值

# 在每个迭代步骤中更新权重和偏置
for t in range(num_iterations):
    # 计算梯度 g

    # 更新一阶矩估计
    m = beta1 * m + (1 - beta1) * g

    # 更新二阶矩估计
    v = beta2 * v + (1 - beta2) * (g ** 2)

    # 修正一阶矩估计的偏差
    m_hat = m / (1 - beta1 ** t)

    # 修正二阶矩估计的偏差
    v_hat = v / (1 - beta2 ** t)

    # 计算权重和偏置的修正量
    delta = -learning_rate * m_hat / (np.sqrt(v_hat) + epsilon)

    # 更新权重和偏置
    weights += delta

三、检测的实现

       由于缺乏现有适用的数据集，我决定亲自收集数据并创建一个全新的数据集，专门用于天气预测系统的研究。数据来源为成都市气象局公布的深成都日数据，包括2020年至2023年的最低湿度、最低气压、最高气温、最高气压、最大风速和最低气温等天气条件指标。为了进一步分析这些指标，采用了EMD方法进行逐个指标的分解。在选择变量后，使用LSTM网络结合三种不同的注意力机制进行了对比实验，以实现多变量的预测。

相关代码示例：

# 对每个指标进行EMD分解
emd = EMD()
X_emd = []
for i in range(X.shape[2]):
    imf = emd(X[:, :, i])
    X_emd.append(imf)

# 将分解后的数据集进行重构，形状为 (样本数, 时间步长, 特征数)
X_emd = np.array(X_emd).transpose((1, 2, 0))

# 划分训练集和测试集
train_size = int(0.8 * X_emd.shape[0])
X_train = X_emd[:train_size]
y_train = y[:train_size]
X_test = X_emd[train_size:]
y_test = y[train_size:]

# 创建LSTM模型
model = Sequential()
model.add(LSTM(units=64, input_shape=(X_train.shape[1], X_train.shape[2]), return_sequences=True))
model.add(Attention())  # 添加注意力机制
model.add(Dense(units=1))

        观察每年各个指标的月度数据分布后发现它们具有明显的相关性和季节趋势。为了进一步研究它们之间的相关性，进行了KMO相关性检验，结果显示相关系数大于0.6，表明这些变量之间存在一定的相关性。为了消除季节趋势，采用了EMD方法对数据进行分解，得到了平稳性序列。这些分析方法可以帮助我们更好地理解各个指标之间的关系，并为进一步预测和分析提供基础。

       数据采集统计了2020年1月1日至2023年6月30日的深圳每日天气特征数据，约有1640条数据，其中缺失数据仅占不到2%。观察成都市天气数据特征发现，每天的各天气指标特征与前一天的天气特征数据差别及变化起伏不明显。基于这一观察，针对有缺失值的数据，可以使用前一天的数据进行填充。这样的处理方法可以有效地填补个别缺失数据，并且考虑到了天气数据的稳定性和连续性。

模型利用超参数优化算法（Adam算法）来确定最优的迭代次数。

相关代码示例：

# 定义超参数和迭代次数的范围
learning_rates = [0.001, 0.01, 0.1]
n_iterations = [10, 20, 30]

best_mse = float('inf')
best_lr = None
best_n_iterations = None

# 遍历超参数的组合
for lr in learning_rates:
    for n_iter in n_iterations:
        # 创建模型
        model = Sequential()
        model.add(Dense(units=64, activation='relu', input_dim=X.shape[1]))
        model.add(Dense(units=1))

        # 编译模型
        optimizer = Adam(lr=lr)
        model.compile(optimizer=optimizer, loss='mean_squared_error')

        # 训练模型
        model.fit(X, y, epochs=n_iter, batch_size=32, verbose=0)

        # 在训练集上进行预测
        y_pred = model.predict(X)

        # 计算均方误差
        mse = mean_squared_error(y, y_pred)

        # 更新最优参数
        if mse < best_mse:
            best_mse = mse
            best_lr = lr
            best_n_iterations = n_iter

# 打印最优超参数和迭代次数
print("Best Learning Rate:", best_lr)
print("Best Number of Iterations:", best_n_iterations)

创作不易,欢迎点赞、关注、收藏。

毕设帮助，疑难解答，欢迎打扰！

最后