【brainpy学习笔记】突触可塑性模型2——Hebb学习律、Oja法则与BCM法则

在生物体中，神经元之间的连接强度会随着时间变化，这种性质被称为突触可塑性。也就是说，刺激的时间不同，即使刺激的类型的强度相同，也会在突触后膜上产生不同的电流效应。根据连接强度变化维持的时长，将突触可塑性分为短时程可塑性与长时程可塑性。本文介绍了Hebb学习律、Oja法则和BCM法则。

Fellyhosn

1707人浏览 · 2023-05-11 16:20:12

Fellyhosn · 2023-05-11 16:20:12 发布

参考书目：《神经计算建模实战——基于brainpy》吴思

书接上文：

【brainpy学习笔记】突触可塑性模型1——STP/STDP模型_Fellyhosn的博客-CSDN博客https://blog.csdn.net/Fellyhosn/article/details/130594605?spm=1001.2014.3001.5501

2.3 Hebb学习律

Hebb学习法则由加拿大心理学家Hebb提出：当神经元A向神经元B产生持续重复的刺激时，A和B的连接强度将增加。

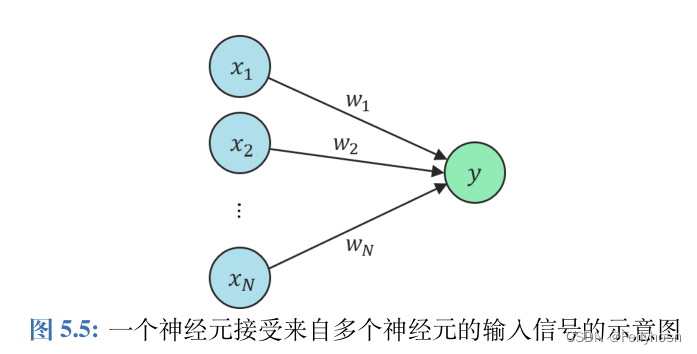
假设有N个神经元和目标神经元连接，其受到第i个神经元的输入为 $x_i$ ，且该神经元对所有输入的相应y可以视为这些输入的线性叠加： $y=\displaystyle\sum_{i=1}^Nw_ix_i$ 。用矩阵形式表示： $y=x^Tw$ ，根据Hebb学习法则，连接权重w的改变量表示为： $\frac{dw}{dt}=\eta x y$ ，η表示学习率。

Hebb学习律指出神经元之间的连接可以通过无监督的方式习得，只要两个相连神经元的输入在时间上具有统计一致性，这两个神经元的连接自然会增强。其缺陷在于不稳定性，w可能会无限增长。其实现代码如下：

class Hebb(bp.dyn.TwoEndConn):
    def __init__(self, pre, post, conn, eta=0.05, delay_step=0, method='exp_auto', **kwargs):
        super(Hebb, self).__init__(pre=pre, post=post, conn=conn, **kwargs)
        self.eta = eta
        self.delay_step = delay_step
        self.pre_ids, self.post_ids = self.conn.require('pre_ids', 'post_ids')
        num = len(self.pre_ids)
        self.w = bm.Variable(bm.random.uniform(size=num) * 2. / bm.sqrt(num))
        self.w_max = bm.Variable(bm.ones(num)*5)
        self.delay = bm.LengthDelay(self.pre.r, delay_step)  # 延迟处理器
        self.integral = bp.odeint(self.derivative, method=method)

    def derivative(self, w, t, x, y):
        dwdt = self.eta * y * x
        return dwdt

    def update(self, tdi):
        t, dt = tdi.t, tdi.dt
        delayed_pre_r = self.delay(self.delay_step)
        self.delay.update(self.pre.r)  # 突触前信号延迟delayed_pre_r时长
        weight = bm.pre2syn(delayed_pre_r, self.pre_ids) * self.w  # 计算每个突触对应突触后神经元反应
        post_r = bm.syn2post_sum(weight, self.post_ids, self.post.num)  # 每个突触后神经元i对yi求和
        self.post.r.value += post_r
        self.w.value = self.integral(self.w, t, self.pre.r[self.pre_ids], self.post.r[self.post_ids], dt)

2.4 Oja法则

在Hebb学习律的基础上，保留了原方程的第五项和第六项，其数学表达式为： $\frac{dw}{dt}=\eta y (x-yw)$ 。为了解决w无限增长的问题，Oja法则在每次更新时对w进行标准化操作，使得 $\|w\|=1$ 。当神经元学习达到稳定时 $\frac{dw}{dt}=0$ ，此时w会成为 $xx^T$ 的最大特征值对应的标准化特征向量，即神经元学习到了输入信号的主成分分量。

用brainpy实现Oja法则：

class Oja(bp.dyn.TwoEndConn):
    def __init__(self,pre,post,conn,eta=0.05,delay_step=0,method='exp_auto',**kwargs):
        super(Oja,self).__init__(pre=pre,post=post,conn=conn,**kwargs)
        self.eta = eta
        self.delay_step = delay_step
        self.pre_ids,self.post_ids = self.conn.require('pre_ids','post_ids')
        num = len(self.pre_ids)
        self.w = bm.Variable(bm.random.uniform(size=num)*2./bm.sqrt(num))
        self.delay = bm.LengthDelay(self.pre.r,delay_step) #延迟处理器
        self.integral = bp.odeint(self.derivative,method=method)
    def derivative(self,w,t,x,y):
        dwdt = self.eta*y*(x-y*w)
        return dwdt
    def update(self,tdi):
        t,dt = tdi.t,tdi.dt
        delayed_pre_r = self.delay(self.delay_step)
        self.delay.update(self.pre.r)#突触前信号延迟delayed_pre_r时长
        weight = bm.pre2syn(delayed_pre_r,self.pre_ids)*self.w #计算每个突触对应突触后神经元反应
        post_r = bm.syn2post_sum(weight,self.post_ids,self.post.num) #每个突触后神经元i对yi求和
        self.post.r.value += post_r
        self.w.value = self.integral(self.w,t,self.pre.r[self.pre_ids],self.post.r[self.post_ids],dt)

在使用Hebb学习法则和Oja法则时，突触前和突触后的模型采用的是发放率模型而不是脉冲神经元模型，这里是简单的发放率模型的实现：

class FR(bp.dyn.NeuGroup):
    def __init__(self,size,**kwargs):
        super(FR,self).__init__(size=size,**kwargs)
        self.r = bm.Variable(bm.zeros(self.num))
        self.input = bm.Variable(bm.zeros(self.num))
    def update(self,tdi):
        self.r.value = self.input
        self.input[:] = 0.

模拟时设定32个突触前神经元，观察w模长变化以及w与x夹角变化，并观察w与x的主成分分量夹角变化：

import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt
import numpy as np

class Oja(bp.dyn.TwoEndConn):
    def __init__(self,pre,post,conn,eta=0.05,delay_step=0,method='exp_auto',**kwargs):
        super(Oja,self).__init__(pre=pre,post=post,conn=conn,**kwargs)
        self.eta = eta
        self.delay_step = delay_step
        self.pre_ids,self.post_ids = self.conn.require('pre_ids','post_ids')
        num = len(self.pre_ids)
        self.w = bm.Variable(bm.random.uniform(size=num)*2./bm.sqrt(num))
        self.delay = bm.LengthDelay(self.pre.r,delay_step) #延迟处理器
        self.integral = bp.odeint(self.derivative,method=method)
    def derivative(self,w,t,x,y):
        dwdt = self.eta*y*(x-y*w)
        return dwdt
    def update(self,tdi):
        t,dt = tdi.t,tdi.dt
        delayed_pre_r = self.delay(self.delay_step)
        self.delay.update(self.pre.r)#突触前信号延迟delayed_pre_r时长
        weight = bm.pre2syn(delayed_pre_r,self.pre_ids)*self.w #计算每个突触对应突触后神经元反应
        post_r = bm.syn2post_sum(weight,self.post_ids,self.post.num) #每个突触后神经元i对yi求和
        self.post.r.value += post_r
        self.w.value = self.integral(self.w,t,self.pre.r[self.pre_ids],self.post.r[self.post_ids],dt)

class Hebb(bp.dyn.TwoEndConn):
    def __init__(self, pre, post, conn, eta=0.05, delay_step=0, method='exp_auto', **kwargs):
        super(Hebb, self).__init__(pre=pre, post=post, conn=conn, **kwargs)
        self.eta = eta
        self.delay_step = delay_step
        self.pre_ids, self.post_ids = self.conn.require('pre_ids', 'post_ids')
        num = len(self.pre_ids)
        self.w = bm.Variable(bm.random.uniform(size=num) * 2. / bm.sqrt(num))
        self.w_max = bm.Variable(bm.ones(num)*5)
        self.delay = bm.LengthDelay(self.pre.r, delay_step)  # 延迟处理器
        self.integral = bp.odeint(self.derivative, method=method)

    def derivative(self, w, t, x, y):
        dwdt = self.eta * y * x
        return dwdt

    def update(self, tdi):
        t, dt = tdi.t, tdi.dt
        delayed_pre_r = self.delay(self.delay_step)
        self.delay.update(self.pre.r)  # 突触前信号延迟delayed_pre_r时长
        weight = bm.pre2syn(delayed_pre_r, self.pre_ids) * self.w  # 计算每个突触对应突触后神经元反应
        post_r = bm.syn2post_sum(weight, self.post_ids, self.post.num)  # 每个突触后神经元i对yi求和
        self.post.r.value += post_r
        self.w.value = self.integral(self.w, t, self.pre.r[self.pre_ids], self.post.r[self.post_ids], dt)
       # mask = (self.w > self.w_max)
       # self.w = bm.where(mask, self.w_max, self.w)

class FR(bp.dyn.NeuGroup):
    def __init__(self,size,**kwargs):
        super(FR,self).__init__(size=size,**kwargs)
        self.r = bm.Variable(bm.zeros(self.num))
        self.input = bm.Variable(bm.zeros(self.num))
    def update(self,tdi):
        self.r.value = self.input
        self.input[:] = 0.
def run_FR(syn_model,I_pre,dur,ax,label,**kwargs):
    num_pre = I_pre.shape[1]
    pre = FR(num_pre)
    post = FR(1)
    syn = syn_model(pre,post,conn=bp.conn.All2All(),**kwargs)
    net = bp.dyn.Network(pre=pre,post=post,syn=syn)
    runner = bp.dyn.DSRunner(net,inputs=[('pre.input',I_pre,'iter')],monitors=['pre.r','post.r','syn.w'])
    runner(dur)
    plt.sca(ax)
    plt.plot(runner.mon.ts,np.sqrt(np.sum(np.square(runner.mon['syn.w']),axis=1)),label=label)
    return runner
def visualize_cos(ax,x,w,step,label,linestyle='.-'):#计算夹角
    a2 = np.sum(x*x,axis=1)
    b2 = np.sum(w*w,axis=1)
    cos_m = np.sum(x*w,axis=1)/np.sqrt(a2*b2)
    plt.sca(ax)
    plt.plot(step,np.abs(cos_m),linestyle,label=label)
    plt.xlabel('time steps')
bm.random.seed(299)
n_pre = 32
num_sample = 20#挑选20个点可视化
dur = 100.
n_steps = int(dur/bm.get_dt())
I_pre = bm.random.normal(scale=0.1,size=(n_steps,n_pre))+bm.random.uniform(size=n_pre)
step_m = np.linspace(0,n_steps-1,num_sample).astype(int)
x = np.asarray(I_pre)[step_m]
_,(ax1,ax2)=plt.subplots(1,2,figsize=(12,4))

runner = run_FR(Hebb,I_pre,dur,ax1,'Hebb learning',eta=0.003)
w = runner.mon['syn.w'][step_m]
visualize_cos(ax2,x,w,step_m,'cos($x,w$) - Hebb learning')

runner = run_FR(Oja,I_pre,dur,ax1,'Oja\'rule',eta=0.003)
w = runner.mon['syn.w'][step_m]
visualize_cos(ax2,x,w,step_m,'cos($x,w$) - Oja\'rule')

C = np.dot(x.T,x)
eigvals,eigvecs = np.linalg.eig(C)
#特征值与特征向量
eigvals,eigvecs = eigvals.real,eigvecs.T.real
largest = eigvecs[np.argsort(eigvals)[-1]]
visualize_cos(ax2,x,np.ones((num_sample,n_pre))*largest,step_m,'cos($x,v_1$)',linestyle='--')
ax1.set_xlabel('t(ms)')
ax1.set_ylabel('$||w||$')
ax1.legend()
ax2.legend()
plt.tight_layout()
plt.show()

结果如下：

左图表示w的模长，可以看出，Oja法则中w的模长始终在1附近，而Hebb学习律的w模长呈现指数增长。右图是两种模型中w和x夹角随时间步长变化，w与x的夹角不断接近0，v1为学习到的主成分，Oja模型下稳定后cos(x,w)与cos(x,v1)十分接近，说明Oja法则确实学习到了x的主成分。

因此，Oja法则可以作为Hebb学习律的一种改进。

2.5 BCM法则

BCM法则保留了更多的高阶项同时实现突触权重增强与抑制，其基于Hebb学习法则，但是可以模拟LTP与LTD，并且LTP和LTD的界限是根据神经元的整体发放频率动态调整的。其数学表达式如下： $\frac{dw}{dt}=\eta y (y-\theta_M)x-\epsilon w$ ，其中 $\theta_M = E^p[y/y_o]$ 表示一个阈值，它根据突触后神经元的响应来决定连接是被增强还是被抑制。 $-\epsilon w$ 为衰减项，用来避免w的发散。p为指数， $y_o$ 为y的缩放系数， $\frac{dw}{dt}$ 随y的变化如下图：

取 $p=1,y_o=1,\epsilon=0$ ， $E^p[y/y_o]$ 的计算方法为取前一段时间的平均发放频率。模拟突触前两个神经元交替发放，且第一个神经元的发放率高于第二个神经元，brainpy实现代码如下：

import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt
import numpy as np

class BCM(bp.dyn.DynamicalSystem):
    def __init__(self,num_pre,num_post,eta=0.01,eps=0.,p=1,y_o=1.,
                 w_max=2.,w_min=-2.,method='exp_auto'):
        super(BCM,self).__init__()
        self.eta = eta
        self.eps = eps
        self.p = p
        self.y_o = y_o
        self.w_max = w_max
        self.w_min = w_min
        self.pre = bm.Variable(num_pre)
        self.post = bm.Variable(num_post)
        self.post_mean = bm.Variable(self.post.value) #突触后平均发放率
        self.w = bm.Variable(bm.ones((num_pre,num_post)))
        self.theta_M = bm.Variable(num_post)
        self.integral = bp.odeint(f=self.derivative,method=method)
    def derivative(self,w,t,x,y,theta):
        dwdt = self.eta*y*(y-theta)*bm.reshape(x,(-1,1)) - self.eps*w
        return dwdt
    def update(self,tdi):
        t,dt,i = tdi.t,tdi.dt,tdi.i
        w = self.integral(self.w,t,self.pre,self.post,self.theta_M,dt)
        w = bm.where(w>self.w_max,self.w_max,w)
        w = bm.where(w<self.w_min,self.w_min,w)
        #w限制范围
        self.w.value = w
        self.post.value = self.pre @ self.w
        self.post_mean.value = (self.post_mean*(i+1)+self.post)/(i+2)
        self.theta_M.value = bm.power(self.post_mean,self.p)
I1,dur = bp.inputs.constant_input([(1.5,20.),(0.,20.)]*5)
I2,_ = bp.inputs.constant_input([(0.,20.),(1.,20.)]*5)
I_pre = bm.stack((I1,I2)).T
model = BCM(num_pre=2,num_post=1,eps=0.)
def f_input(tdi):model.pre.value = I_pre[tdi.i]
runner = bp.dyn.DSRunner(model,inputs=f_input,monitors=['pre','post','w','theta_M'],
                         fun_monitors={'w':lambda tdi:model.w.flatten()})
runner.run(dur)

fig, gs = bp.visualize.get_figure(9, 1, 0.5, 6.)
ax = fig.add_subplot(gs[0:3, 0])
plt.plot(runner.mon.ts, runner.mon['pre'][:,0], label='pre0', color='r')
plt.plot(runner.mon.ts, runner.mon['pre'][:,1], label='pre1', color='k',linestyle='--')
plt.legend(loc='upper right')
plt.title('BCM model')
plt.xticks([])
ax.spines['top'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['right'].set_visible(False)
ax = fig.add_subplot(gs[3:6, 0])
plt.plot(runner.mon.ts, runner.mon['post'][:,0], label='post0', color='g')
plt.plot(runner.mon.ts, runner.mon['theta_M'], label='theta_M', color='b',linestyle='--')
plt.legend(loc='upper right')
plt.xticks([])
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax = fig.add_subplot(gs[6:9, 0])
plt.plot(runner.mon.ts, runner.mon['w'][:,0], label='w0', color='r')
plt.plot(runner.mon.ts, runner.mon['w'][:,1], label='w1', color='k',linestyle='--')
plt.legend(loc='upper right')
plt.xticks([])
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.xlabel('Time [ms]')
plt.show()

模拟结果如下：

由于两个神经元交替兴奋，当突触前第0号神经元pre0强烈兴奋时，突触后神经元（post0）活动高于平均历史活动theta_M，学习规则呈现长时程增强；当突触前第一号神经元pre1微弱兴奋时，突触后神经元的活动低于平均历史活动，学习规则呈现长时程减弱，使得w1逐渐降低。

在BCM法则中，连接权重的增减并不是因为神经元的发放频率达到某一阈值，而是取决于其发放频率是否超过过去一段时间的平均发放频率，体现了BCM法则的适应性。

3 总结

突触可塑性模型使得神经元的连接强度发生变化（即连接权重w动态变化），根据维持的时间分为短时程可塑性STP和长时程可塑性LTP。STP主要由突触前神经元内部暂时的变化引起，而LTP的产生需要在生化层面发生变化。目前模拟LTP现象的模型大都是从其现象入手，而非内部的产生机制，例如STDP模型、Hebb学习罚则、Oja法则、BCM法则等。