实验六 ：DBSCAN聚类方法

一、实验目的

掌握DBSCAN聚类方法的基本理论，通过编程对实例进行聚类。

二、实验任务

对DBSCAN聚类方法进行编码计算，实例如下：

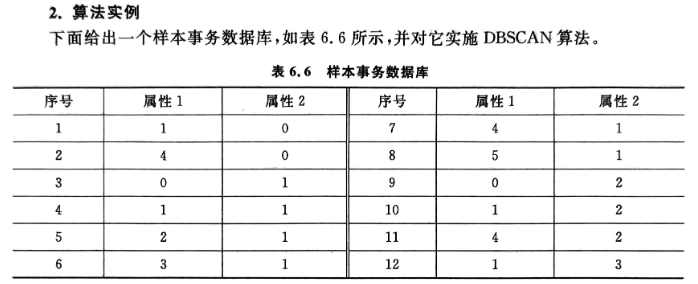
三、实验过程

1.DBSCAN聚类模型介绍：

2.具体步骤介绍：

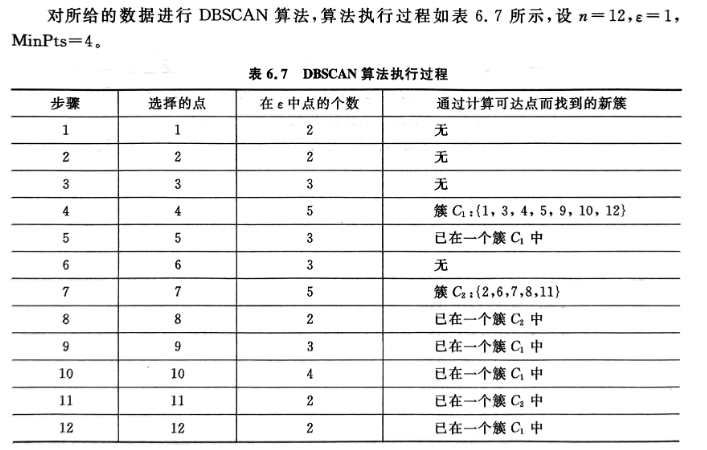
四、实验结果

实现平台：Matlab 2022A

实验代码：

% 示例数据
data = [
    1, 0;
    4, 0;
    0, 1;
    1, 1;
    2, 1;
    3, 1;
    4, 1;
    5, 1;
    0, 2;
    1, 2;
    4, 2;
    1, 3;
];

% 设置参数
epsilon = 1;
minPts = 4;

% 调用DBSCAN算法
result_clusters = dbscan(data, epsilon, minPts);

% 显示结果
fprintf('DBSCAN聚类结果：\n');
for i = 1:length(result_clusters)
    fprintf('簇 %d：\n', i);
    disp(result_clusters{i});
end

% 定义DBSCAN算法函数
function clusters = dbscan(data, epsilon, minPts)
    n = size(data, 1); % 数据库中数据对象的数量
    labels = zeros(n, 1); % 初始化标签为0，表示未分类
    cluster_id = 0; % 初始化簇ID
    
    % 计算距离矩阵
    D = pdist2(data, data);
    
    % 遍历每个点
    for i = 1:n
        if labels(i) ~= 0 % 如果该点已经分类，跳过
            continue;
        end
        
        % 找到epsilon范围内的所有点
        neighbors = find(D(i, :) <= epsilon);
        
        if numel(neighbors) < minPts % 如果邻居数量少于minPts，将其标记为噪声
            labels(i) = -1;
            continue;
        end
        
        % 形成一个新簇
        cluster_id = cluster_id + 1;
        labels(i) = cluster_id;
        
        % 处理该簇的所有邻居点
        j = 1;
        while j <= numel(neighbors)
            neighbor_idx = neighbors(j);
            
            if labels(neighbor_idx) == -1 % 如果邻居点是噪声点，将其归为当前簇
                labels(neighbor_idx) = cluster_id;
            end
            
            if labels(neighbor_idx) == 0 % 如果邻居点未分类
                labels(neighbor_idx) = cluster_id;
                
                % 找到邻居点的新邻居
                new_neighbors = find(D(neighbor_idx, :) <= epsilon);
                if numel(new_neighbors) >= minPts
                    neighbors = [neighbors, new_neighbors]; % 将新的邻居加入到邻居列表中
                    neighbors = unique(neighbors, 'stable'); % 去重并保持顺序
                end
            end
            
            j = j + 1;
        end
    end
    
    % 将结果转换为簇的格式
    clusters = arrayfun(@(c) data(labels == c, :), unique(labels(labels > 0)), 'UniformOutput', false);
end

实验结果：

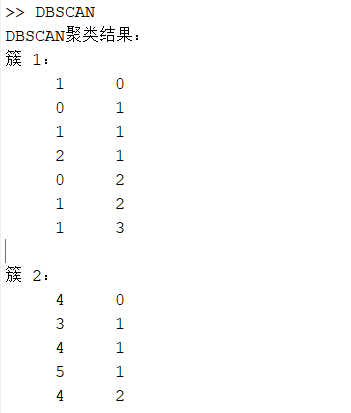
五、个人总结

1.对DBSCAN聚类方法的理解

和传统的K-Means算法相比，DBSCAN最大的不同就是不需要输入类别数k，最大的优势是可以发现任意形状的聚类簇，而不是像K-Means，一般仅仅使用于凸的样本集聚类。同时它在聚类的同时还可以找出异常点，这点和BIRCH算法类似。一般来说，如果数据集是稠密的，并且数据集不是凸的，那么用DBSCAN会比K-Means聚类效果好很多。如果数据集不是稠密的，则不推荐用DBSCAN来聚类。

（1）DBSCAN的优点：

1） 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

2） 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

（2）DBSCAN的缺点：

1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

2） 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

3） 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响

2.对编码实现过程的回顾

一开始编写这个代码的时候，完全按着书上的逻辑走，我写了很多循环，重复计算了很多次欧氏距离等，导致整个代码的效率很低下，十几分钟也没能跑出来。后来对代码进行了优化，采用矩阵运算来替换循环，也简化了聚类的生成过程，避免一些不必要的循环操作。同时采用标签数组进行簇的标记，更清晰和高效。neighbors和new_neighbors要做水平拼接避免矩阵维度不一致。可以使用 unique 函数的 stable选项确保删除重复值的同时保持原有顺序。