进行模逆运算(python，欧几里得算法，Stein算法)

欧几里得算法的关键在于，利用这一性质不断迭代，直到a' % b' = 0时，对应的b'即为a与b的最大公约数。

the_universe_

1295人浏览 · 2024-07-09 11:18:15

the_universe_ · 2024-07-09 11:18:15 发布

一、欧几里得

1、欧几里得算法求最大公约数

欧几里得算法的关键在于gcd(a, b) = gcd(b, a%b)，利用这一性质不断迭代，直到a' % b' = 0时，对应的b'即为a与b的最大公约数

设a = b * k + r
gcd(a, b) = gcd(b*k+r, b)
        = gcd(r, b)
        = gcd(a%b, b)

代码

def gcd(x, y):
    while y:
        t = x % y
        x = y
        y = t 
    return x
    
# Example usage:
a = random.randint(1, 5000000)
m = random.randint(1, 5000000)
print(gcd(a, m))

2、扩展欧几里得算法求逆元

求v模u的逆元即求令v*s + u*t =1 的s

扩展欧几里得算法求逆元本质还是利用欧几里得算法，欧几里得算法中参数只有u, v我们现在再增加四个参数，令

 (x1, x2, x3) = (1, 0, v)

  (y1, y2, y3) = (0, 1, u)

满足等式:

  x1*v + x2*u = x3                           (1)

  y1*v + y2*u = y3                           (2)

然后还是执行欧几里得算法的迭代过程，令v' = u 即 x3' = y3，u' = v%u 即 y3' = x3 - [x3 / y3] * y3

为保证等式(1)，(2)的成立，所以对于x1, x2执行与x3同样的操作，对于y1, y2执行与y3同样的操作

最后结束迭代的条件与欧几里得算法略有差别，由于我们要找到令v*s + u*t =1 的 s所以临界条件

为y3 = 1此时y1*v + y2*u = 1所以所求逆元即为y1

当然如果不存在y3 = 1直接得到y3 = 0则说明v与u不互质，也就不存在逆元了

代码

import random


def inverse(v, u):
    x1, x2, x3 = 1, 0, v
    y1, y2, y3 = 0, 1, u
    while 1:
        if y3 == 0:
            return -1
        elif y3 == 1:
            return y1 % u
        q = x3 // y3
        t1, t2, t3 = (x1 - q * y1), (x2 - q * y2), (x3 - q * y3)
        x1, x2, x3 = y1, y2, y3
        y1, y2, y3 = t1, t2, t3


# Example usage:
a = random.randint(1, 5000000)
m = random.randint(1, 5000000)
print(inverse(a, m))

二、Stein

1、Stein算法求最大公约数

首先要了解什么是stein算法，stein算法本身是求解最大公因数的算法

定义：(摘自百度百科)Stein算法是一种计算两个数最大公约数的算法，是针对欧几里德算法在对大整数进行运算时，需要试商导致增加运算时间的缺陷而提出的改进算法

Stein算法的关键就在于除2操作，具体表现如下：

a偶b偶：gcd(a, b) = 2 * gcd(a/2, b/2)

a偶b奇：gcd(a, b) = gcd(a/2, b)

a奇b偶：gcd(a, b) = gcd(a, b/2)

a奇b奇：gcd(a, b) = gcd(|a-b|, min{a, b})

（当a为奇数，b为奇数时 |a-b| 就是在构造 '2' ，然后继续除2操作）

利用这一性质不断迭代，直到 |a' - b'| = 0时，对应的min{a', b'}即为a与b的最大公约数

上述步骤中，大部分都比较简单，在这里解释一下第7点：

设gcd(a, b)=x, a=px, b=qx, 且a>b
a, b均为奇数，所以p, q, x也都是奇数,
|a-b|=(p-q)x   ,|p-q|为偶数
所以|p-q|x 与 qx的最大公约数也为x
gcd(a, b) = gcd(|a-b|, min{a, b})
//这里换为max{a, b}依然成立, 只是我们的目的是将大数不断减小，所以选择min{a, b}
到此时其实可以结束了, 但已知一定有|a-b|为偶数, min{a, b}为奇数,
按照运算规则, 我们直接运行第5条, |a-b| -> |a-b|/2, min{a, b}不变, 就可以减少一次循环

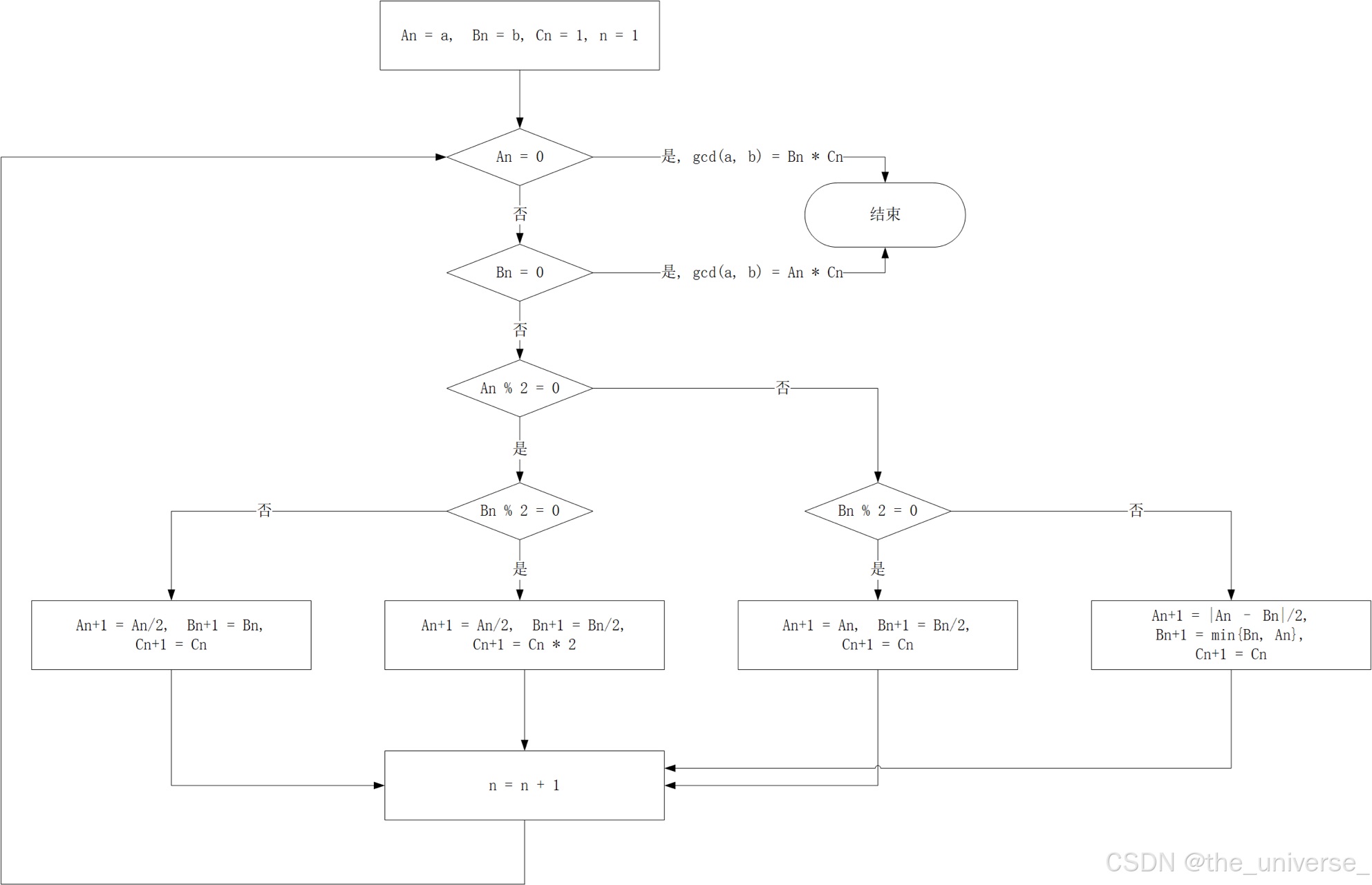
流程图如下所示：

代码

def stein(a, b, c):
    if a == 0:
        return b * c
    elif b == 0:
        return a * c
    else:
        if a % 2 == 0:
            if b % 2 == 0:
                c = c * 2
                a = a / 2
                b = b / 2
            else:
                a = a / 2
        elif b % 2 == 0:
            b = b / 2
        else:
            l = a
            a = abs(a - b) / 2
            b = min(l, b)
        return stein(a, b, c)


# Example usage:
a = random.randint(1, 5000000)
m = random.randint(1, 5000000)
print(stein(a, m))

2、扩展Stein算法求逆元

理解了上面的内容，这一部分就很好理解了，类似于扩展欧几里得算法，构造了

x1*v + x2*u = x3                     (1)
y1*v + y2*u = y3                     (2)

我们只要令x3或y3为1，即可得到v*s + u*t = 1，也就求得了逆元

不断进行除2操作，x1, x2, x3都为偶时(1)式整体除2，表现为(x1, x2, x3) = (x1/2, x2/2, x3/2)，同理y1, y2, y3都为偶时(2)式整体除2，表现为(y1, y2, y3) = (y1/2, y2/2, y3/2)

当x3为偶数，而x1, x2不全为偶数时，有

  (x1+u)*v/2 + (x2-v)*u/2
= (x1*v + x2*u + u*v - v*u) / 2
= (x1*v + x2*u) / 2
=  x3 / 2

所以就令x1 = x1 + u, x2 = x2 - v，来构造 '2'，当y3为偶数，而y1, y2不全为偶数时也同理

x3，y3都是奇数时采用两奇数相减的方法再次构造 '2'

最后若是x3 = 1，则有x1*v + x2 * u = x3所以逆元为x1，同理若是y3 = 1则逆元为y1

代码

def ex_stein(v, u):
    # 若不满足a>0且m>1, 则报错AssertionError
    assert v > 0 and u > 1, "a must be positive and m must be greater than 1"
    # 特例：1模任何数的逆元均为1
    if v == 1:
        return 1
    x1, x2, x3 = 1, 0, v
    y1, y2, y3 = 0, 1, u
    while x3 != 1 or y3 != 1:
        if x3 % 2 == 0:
            if x1 % 2 == 0 and x2 % 2 == 0:
                x1, x2, x3 = x1 / 2, x2 / 2, x3 / 2
            else:
                x1 = x1 + u
                x2 = x2 - v
        elif y3 % 2 == 0:
            if y1 % 2 == 0 and y2 % 2 == 0:
                y1, y2, y3 = y1 / 2, y2 / 2, y3 / 2
            else:
                y1 = y1 + u
                y2 = y2 - v
        else:
            if x3 > y3:
                x1, x2, x3 = x1 - y1, x2 - y2, x3 - y3
            else:
                y1, y2, y3 = y1 - x1, y2 - x2, y3 - x3
    if x3 == 1:
        return x1 % u
    else:
        return y1 % u


# Example usage:
a = random.randint(1, 5000000)
m = random.randint(1, 5000000)
print(ex_stein(a, m))

上面两种方法，个人认为欧几里得算法要更易理解且简单一些，仁者见仁，智者见智，大家根据喜好选择