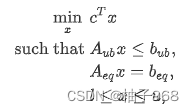
python解决线性规划问题,含例题 使用scipy.linprog
求得目标解与答案一致,但x最优解的取值不同,可能存在多个可行解的问题。下面我们以一个例题来尝试使用该函数解决线性规划问题。scipy官方对于linprog函数的说明文档。
·
from scipy.optimize import linprog
scipy官方对于linprog函数的说明文档
scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='highs', callback=None, options=None, x0=None, integrality=None)
Linear programming solves problems of the following form:

Parameters:
c:1-D array
A_ub:2-D array, optional
b_ub:1-D array, optional
A_eq: 2-D array, optional
b_eq: 1-D array, optional
boundssequence, optional
x: 1-D array
下面我们以一个例题来尝试使用该函数解决线性规划问题。


c=[-70, -50, -60] A_ub = [[2, 4, 3], [3, 1, 5], [7, 3, 5]] b_ub = [150, 160, 200]
result=linprog(c,A_ub=A_ub,b_ub=b_ub,bounds=[(0,None),(0,None),(0,None)],method='highs') result
message: Optimization terminated successfully. (HiGHS Status 7: Optimal) success: True status: 0 fun: -2590.909090909091 x: [ 2.121e+00 1.576e+01 2.758e+01] nit: 3 lower: residual: [ 2.121e+00 1.576e+01 2.758e+01] marginals: [ 0.000e+00 0.000e+00 0.000e+00] upper: residual: [ inf inf inf] marginals: [ 0.000e+00 0.000e+00 0.000e+00] eqlin: residual: [] marginals: [] ineqlin: residual: [ 0.000e+00 0.000e+00 0.000e+00] marginals: [-6.364e+00 -0.000e+00 -8.182e+00] mip_node_count: 0 mip_dual_bound: 0.0 mip_gap: 0.0
求得目标解与答案一致,但x最优解的取值不同,可能存在多个可行解的问题

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)