一、简介

道格拉斯-普客算法 百度百科

二、代码

分享给有需要的人，代码质量勿喷

import numpy as np
import math
import operator
import laspy
import matplotlib.pyplot as plt


class xjPoint():
    def __init__(self, x, y, z, ID):
        self.x = x
        self.y = y
        self.z = z
        self.ID = ID


def DP(dataX, dataY, Tdis):
    point_count = len(dataX)
    k = (dataY[point_count-1]-dataY[0]) / (dataX[point_count-1]-dataX[0])
    b = dataY[0] - k * dataX[0]
    dis_max = -1
    dis_max_index = -1
    for i in range(point_count):
        dis = abs(k*dataX[i]+b-dataY[i]) / math.sqrt(k*k+1)

        # region plot processing（仅仅是绘制过程----------------------------------------）
        ax.cla()
        ax.set_title("Douglas-Peuker")
        ax.set_xlabel("x")
        ax.set_ylabel("y")
        buffer = 1
        plt.xlim(min(X) - buffer, max(X) + buffer)
        plt.ylim(min(Y) - buffer, max(Y) + buffer)
        plt.grid(True)

        # all points
        ax.scatter(X, Y, color='k', label='data')

        # points
        ax.scatter(dataX, dataY, color='b',label='current section')

        # SE Line
        plt.plot([dataX[0], dataX[point_count - 1]], [dataY[0], dataY[point_count - 1]], "r",
                 label='Start-End Line')

        # current point
        plt.plot(dataX[i], dataY[i], "go", markersize=10, label='current point')
        # plt.text(min(data_X)+2, min(data_Y)+4, str(round(dis,3)), fontdict={'size': 15, 'color': 'g'})

        #当前段的节点
        plt.plot(dataX[dis_max_index], dataY[dis_max_index], "ro", markersize=10,
                 label='point_max_dis')

        # 所有已确定的节点
        plt.plot(resultX, resultY, "r*", markersize=12, label='Node')

        plt.legend()
        plt.pause(0.1)
        # endregion

        if dis>=dis_max:
            dis_max = dis
            dis_max_index = i

    if dis_max>Tdis:
        resultX.append(dataX[dis_max_index])
        resultY.append(dataY[dis_max_index])

        dataXX1 = dataX[0:dis_max_index+1]
        dataYY1 = dataY[0:dis_max_index+1]
        DP(dataXX1, dataYY1, Tdis)

        dataXX2 = dataX[dis_max_index:point_count]
        dataYY2 = dataY[dis_max_index:point_count]
        DP(dataXX2, dataYY2, Tdis)


if __name__ == '__main__':
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)


    #region 1 acquire data from las（自己定义数据也可以，但是要排好顺序----------------------）
    # 读
    f = laspy.read('a.las')

    # 偏移值
    lasHeader = f.header
    offsetX = lasHeader.offset[0]
    offsetY = lasHeader.offset[1]

    data_all = []
    maxX = maxY = -99999999
    minX = minY = 99999999
    for i in range(lasHeader.point_records_count):
        p = xjPoint(f.x[i] - offsetX, f.y[i] - offsetY, f.z[i], i)
        data_all.append(p)

        #region 判断XY最大最小值
        if f.x[i]>=maxX:
            maxX = f.x[i]
        if f.x[i]<minX:
            minX = f.x[i]
        if f.y[i]>=maxY:
            maxY = f.y[i]
        if f.y[i]<minY:
            minY = f.y[i]
        #endregion

    #region sort by scale (x or y) important
    if (maxX-minX)>=(maxY-minY):
        collation = operator.attrgetter('x', 'ID')
        data_all.sort(key=collation)
    else:
        collation = operator.attrgetter('y', 'ID')
        data_all.sort(key=collation)
    #endregion

    X = []
    Y = []
    for i in range(len(data_all)):
        X.append(data_all[i].x)
        Y.append(data_all[i].y)
    #endregion


    #region 2 DP（--------------------------=------------------------------）
    resultX = []
    resultY = []
    resultX.append(X[0])
    resultY.append(Y[0])

    T_DIS = 2
    DP(X, Y, T_DIS)

    resultX.append(X[len(X)-1])
    resultY.append(Y[len(Y)-1])
    #endregion


    # region 3 plot result（-----------------------------------）
    ax.cla()
    ax.set_title("Douglas-Peuker")
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    buffer = 1
    plt.xlim(min(X) - buffer, max(X) + buffer)
    plt.ylim(min(Y) - buffer, max(Y) + buffer)
    plt.grid(True)

    # data
    ax.scatter(X, Y, color='k', label='data')

    #节点与连线
    plt.plot(resultX, resultY, "r*", markersize=12, label='Node')
    plt.plot(resultX, resultY, "r", linestyle="dashed", label='Line')

    plt.legend()
    plt.show()
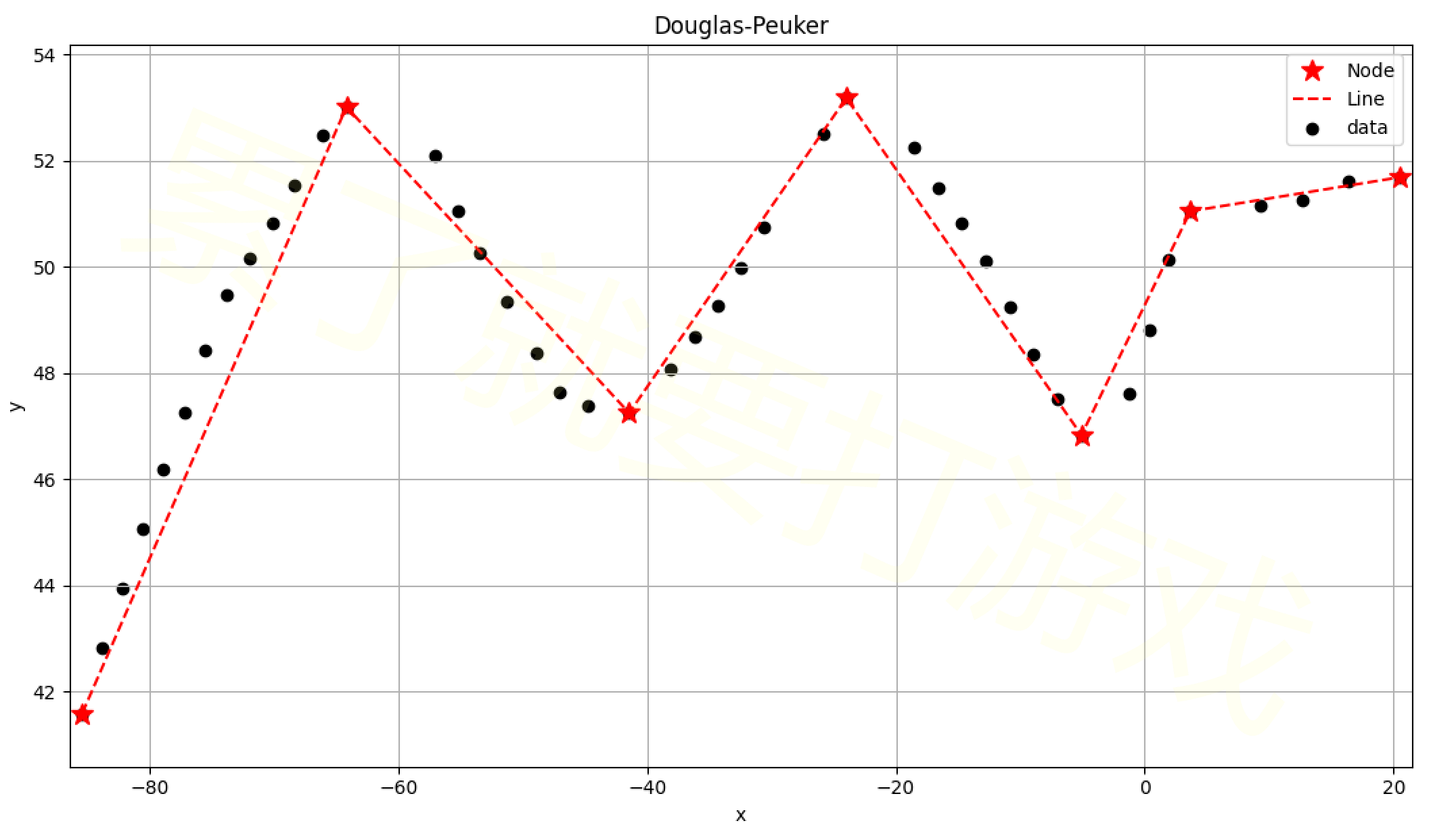
    # endregion

三、试验结果