杂草优化算法及其python实现

简单通俗的杂草算法学习笔记

coffeein-free

1514人浏览 · 2022-05-18 19:12:55

coffeein-free · 2022-05-18 19:12:55 发布

近年来，群智能研究领域出现诸多算法，如蚁群算法、粒子群算法(附完整代码)、蜂群算法、鱼群算法、猫群算法、杂草算法以及布谷鸟算法等。其中，杂草算法代码简单，易于实现，具有较强的自适应性和鲁棒性。

算法步骤：(以搜索最小值为例)

1、初始化种群

随机生成一定数量的初始解(杂草)，这些初始解(杂草)随机地均匀地分布在搜索空间(草原)内。

2、种群繁殖

现实世界中，不同杂草在草原上的适应度不同，适应度高的个体生长旺盛，将会产生更多的子代种子。

对应到最优解搜索问题中，接近最优解的解具有更强的适应度，会产生更多的子代个体(下一代的解)。远离最优解的解具有较低适应度，会产生较少的下一代个体。

基于上述分析，当前解产生子代种子个数公式如下：

其中，Fx代表当前解的适应度，Fmin代表当前种群中所有解的最小适应度，Fmax代表代表当前种群中所有解的最大适应度。seed_max和seed_min分别代表每次迭代过程中单个解能够随机生成的最大/最小种子个数。

注意，当搜索目标函数最大解时，

当搜索目标函数最小解时，

其中Smax代表当前种群目标函数最大值，Smin代表当前种群目标函数最小值。(当搜索最小值的时候，函数值最小的解适应度最大)

3、空间搜索

现实世界中，杂草的种子随着动物的运动、风能等传播到父代个体周围。种子传播的距离服从正态分布。

对应到最优解搜索过程中，当前解的子代服从正态分布，该正态分布的均值为当前解的位置，标准差定义为sigma，sigma随着时间的推移与当前迭代次数g成负相关，在sigma最大值sigma_max、sigma最小值sigma_min、最大迭代次数g_max以及非线性调节因子w给定的情况下：

对应python代码：

sigma_min = 0.01
sigma_max = 10
w = 3

def update_sigma(g):             # 更新sigma，sigma随时间变化越来越小
    ret = sigma_min + ma.pow(((gmax - g) / gmax), w) * (sigma_max - sigma_min)
    return ret

4、竞争淘汰

自然选择按照优胜劣汰原则淘汰掉那些不适应当前环境的个体(杂草)，留下那些适应当前环境的杂草。

对应到最优解搜索过程中，当我们当前解集合大于预设的max_weed_size时，按照优胜劣汰的原则淘汰那些适应度低的解而保留那些适应度高的个体，这样经过数次迭代后该算法能够收敛到最优解。

完整python代码：

以搜索 f(X) = x1 ^ 2 + x2 ^ 2 + x3 ^ 3 + x4 ^ 2 最小值为例 (X_Best = (0,0,0,0))

import numpy as np
import math as ma
import time
delta_init = 5              # 初始方差
delta_end = 0.01            # 结束方差
max_weed_size = 500         # 最大种子数量
w = 3                       # 非线性调节因子
gmax = 30                  # 迭代次数
seed_max = 6                # 最大生成种子数
seed_min = 2                # 最小生成中子数


class weed:                 # 种子
    def __init__(self, x1, x2, x3, x4):     # 初始化
        self.x1 = x1
        self.x2 = x2
        self.x3 = x3
        self.x4 = x4

    def func(self):         # 计算要优化的目标函数值
        ret = ma.pow(self.x1, 2) + ma.pow(self.x2, 2) + ma.pow(self.x3, 4) + ma.pow(self.x4, 2)
        # print(ret)
        return float(ret)

    def random(self, sigma):    # 随机产生在父代个体周围产生子代种子，sigma随时间变化越来越小
        rx1 = self.x1 + np.random.normal(0, sigma, 1)
        rx2 = self.x2 + np.random.normal(0, sigma, 1)
        rx3 = self.x3 + np.random.normal(0, sigma, 1)
        rx4 = self.x4 + np.random.normal(0, sigma, 1)
        return weed(rx1, rx2, rx3, rx4)


def update_sigma(g):             # 更新sigma，sigma随时间变化越来越小
    ret = delta_end + ma.pow(((gmax - g) / gmax), w) * (delta_init - delta_end)
    return ret


def cal_seed_num(fx, fmax, fmin):  # 当前个体适应度越大，产生子代种子个数越多
    ret = (fmax - fx) / (fmax - fmin) * (seed_max - seed_min) + seed_min
    return int(ret)


def main():
    weed_dic = {}                   # 种群通过字典方式保存，Key：Weed(x1, x2, x3, x4), Value: Weed.func()
    for i in range(5):              # 初始化
        w1 = weed(np.random.uniform(-50, 50, 1), np.random.uniform(-50, 50, 1),
                  np.random.uniform(-50, 50, 1), np.random.uniform(-50, 50, 1))
        weed_dic[w1] = w1.func()
    weed_dic = sorted(weed_dic.items(), key=lambda d: d[1], reverse=False)      # 对种群按照value值升序排列
    weed_dic = dict(weed_dic)                                                   # 排列后dict型对象被转换成了list型，将dist再转换成list型
    while len(weed_dic) > max_weed_size:                                        # 如果达到预设的最大种群数量，触发淘汰操作
        weed_dic.popitem()                                                      # 删除最后一个元素，即函数值最大的元素
    for g in range(gmax):
        max_weed = weed_dic.popitem()
        fmax = max_weed[1]                                                      # 获取当前种群中最大函数值
        weed_dic[max_weed[0]] = max_weed[1]
        fmin = None
        sigma = update_sigma(g)                                                  # 更新sigma
        tmp_dict = {}
        for item in weed_dic.items():
            if fmin is None:
                fmin = item[1]                                                   # 获取当前种群中最小函数值
            sn = cal_seed_num(item[1], fmax, fmin)                                 # 计算当前个体产生种子个数
            for itor in range(sn):                                               # 生成新个体
                insert = item[0].random(sigma)
                tmp_dict[insert] = insert.func()
        for item in tmp_dict.items():                                            # 子代个体插入到整个种群个体中
            weed_dic[item[0]] = item[1]
        weed_dic = sorted(weed_dic.items(), key=lambda d: d[1], reverse=False)   # 排序并删除函数值大的个体
        weed_dic = dict(weed_dic)
        while len(weed_dic) > max_weed_size:
            weed_dic.popitem()
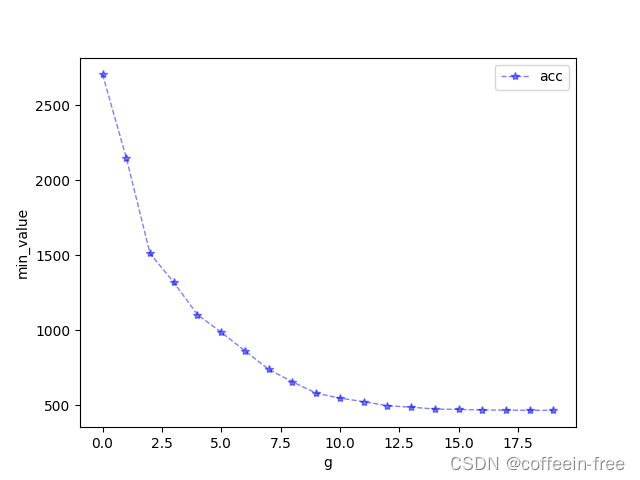
    for item in weed_dic.items():                                                # 迭代结束，打印结果即为目标函数极小值
        print(item[1])
        return item[1]

if __name__ == '__main__':
    start = time.time()
    main()
    end = time.time()
    print(end - start)