1、概括

在故障诊断中，信号频域分析的基本手段公众号基本涵盖，有遗漏的相关方法和技术，知道的小伙伴可以后台私信我，我继续添加！

这次给大家带来的是短时傅里叶变换（Short-Time Fourier Transform，简称STFT），它是傅里叶变换在时频域的扩展，它是为了分析频域随时间变化的非平稳信号。

本文的流程如下图所示，模拟了一个啁啾信号（一个线性调频的信号），并借助matlab的短时傅里叶变换函数stft，分析了其时频特性，绘制了时频图。同时，复现了matlab的stft函数的计算过程，供大家参考。

该内容主要参考了一些资料：

https://ww2.mathworks.cn/help/signal/ref/stft.html?searchHighlight=stft&s_tid=srchtitle_support_results_1_stft

代码采用了Matlab 2024a进行运行，欢迎大家测试和提出问题！

2、具体案例

啁啾(zhōu jiū，英文中为chirp)信号一般是指调频信号，即随着时间的变化，信号的主频在不断发生变化（或增加、或减少）。当这种信号当做音频输出时，听起来会像鸟的唧唧声，所以叫啁啾。

利用matlab的chirp函数生成了一个1s内从100Hz到5000Hz的线性调频信号（啁啾信号），采样频率为24000Hz，具体如下：

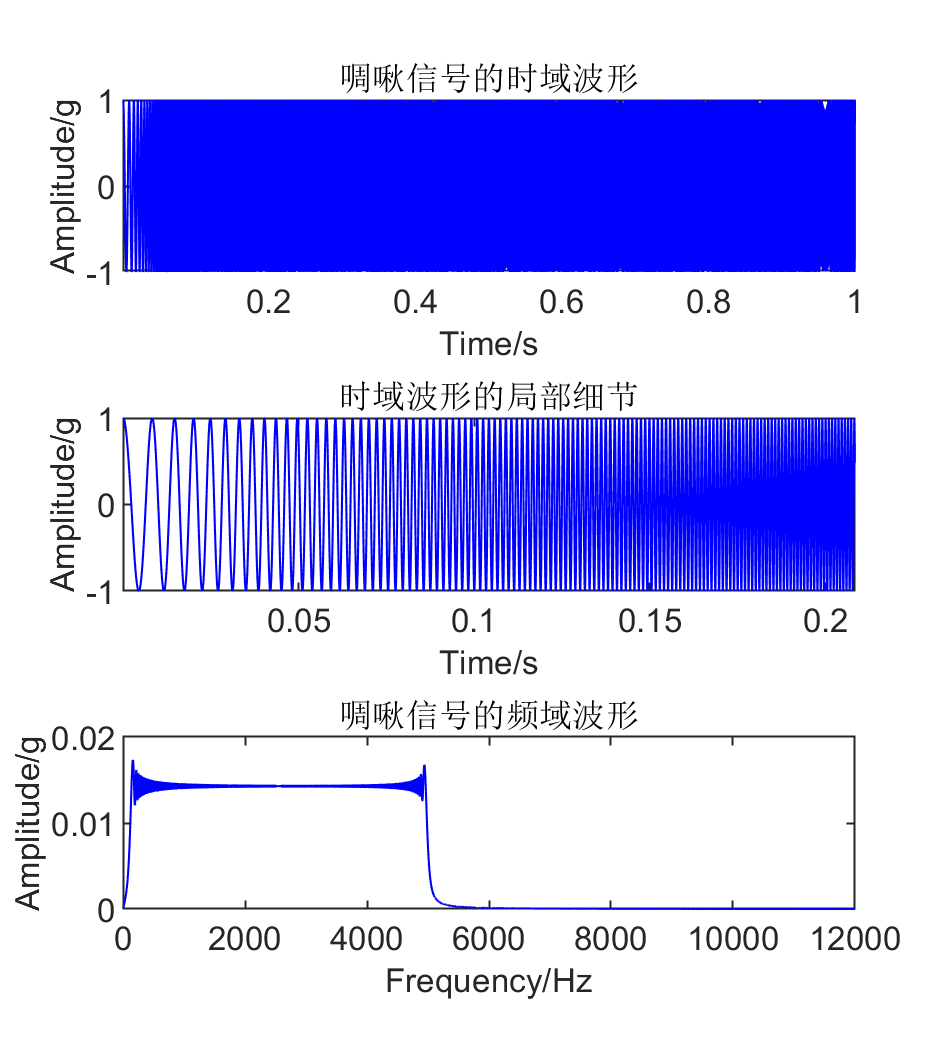
从啁啾信号的局部细节图能发现，随着时间的增长，信号波形越来越密集，即信号的频率逐渐增大。在啁啾信号频谱中，低频占据信号的主频，无法发现信号频率的时变特征。

采用stft函数，设置矩形窗，窗长256，滑动步长设置为128，FFT分析的信号长度与窗长一致，均为256，设置stft函数的FrequencyRange为onesided,即仅分析信号的傅里叶变换的单边频谱，获得的短时傅里叶变换结果如下图。

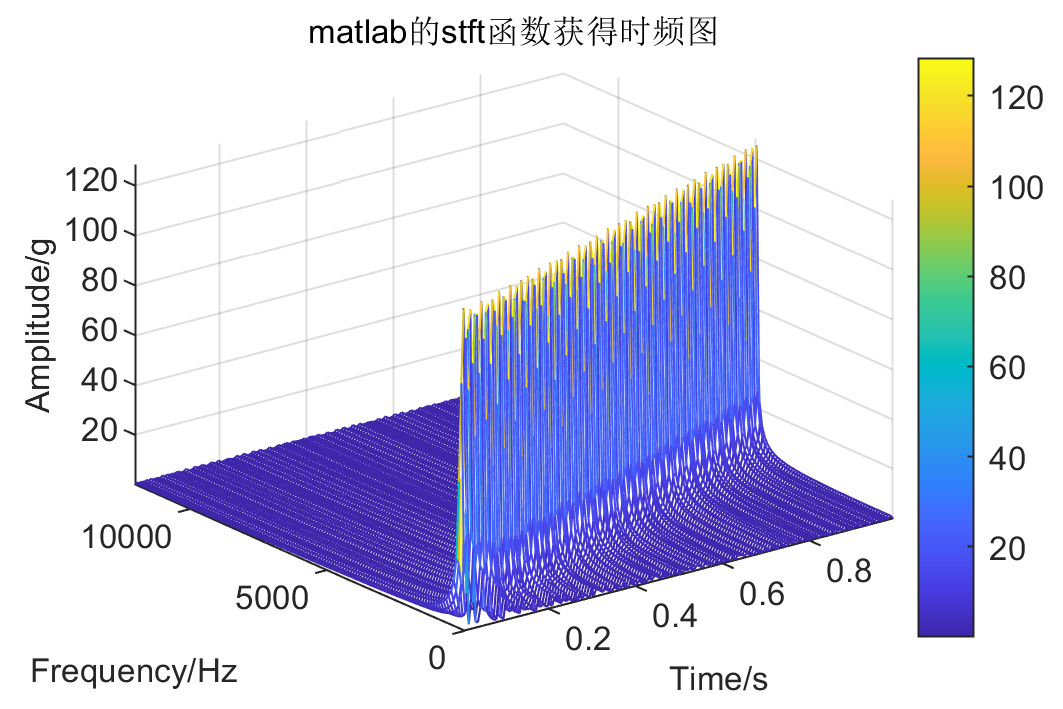
上图分别为短时傅里叶变换的不同画图方式，分别为mesh函数和imagesc函数。从上图中能发现，啁啾信号的频率从100Hz到5000Hz线性增长，这表明短时傅里叶变换能较好地分析该啁啾信号，对比FFT的结果，表明了短时傅里叶变换在信号时频分析方面的优势。

stft函数的计算流程如下，它利用窗函数，将原始信号划分为了若干个子信号，然后分别采用傅里叶变换，获得其对应的频谱，最后将这些频谱按照不同的时间先后顺序进行拼接，绘制了时频图。

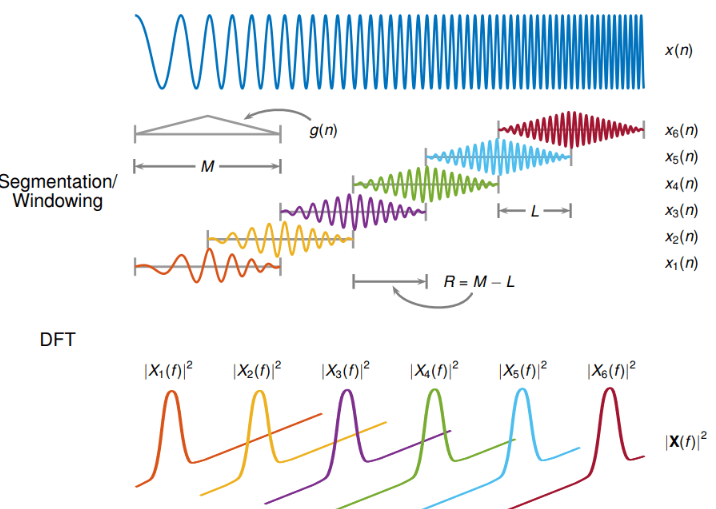
因此，在上述原理基础上，手动复现了stft的计算过程，获得的时频图如下：

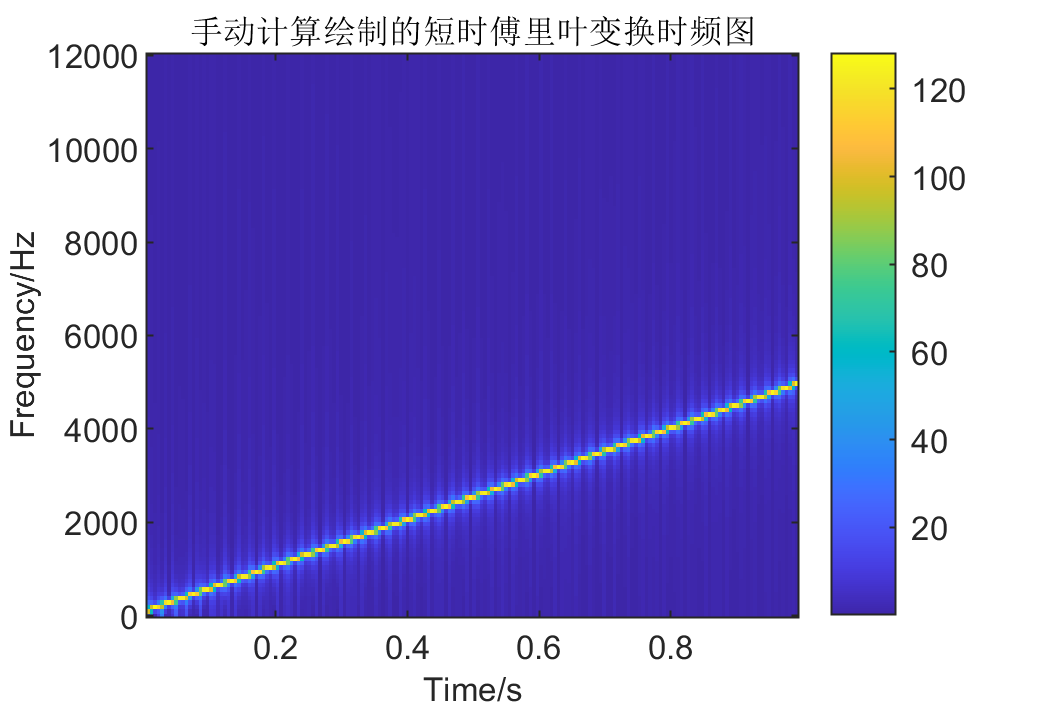
该图与stft获得的时频图是一致的，计算二者的平均偏差结果：（平均偏差为两数差的绝对值的平均数）

从定量结果来看，复现过程结果与函数计算结果一致，验证了复现过程的正确性。

注意：值得注意是，stft函数计算的是子信号的FFT的单边频谱的绝对值，它并未进行信号长度的标准化，就是描述信号的频频幅值，不是能量也不是功率。

3、具体代码

代码主要分为两个：

1、main.m（主函数）

2、frequ_am_phase.m（幅值谱和相位谱计算函数）

说明：

frequ_am_phase.m函数

调用形式：

[freq,P1,Theta]=frequ_am_phase(y,fs,tol)

输入：

信号y，矩阵，行X列=单个信号的采样索引X信号数，比如信号的大小为8192X12，表示一个有12个信号的数据矩阵，每个信号长度为8192。注意，如果仅有一个信号，则y应该是一个列向量。同时，y的行数尽量为偶数，奇数的话会引起程序索引的警告。

     fs:采样频率，标量

     tol:相位阈值参数，标量（可缺省，下面讲解）

输出

freq:表示幅值谱的横轴，向量，HzX1

       P1:表示幅值谱的纵轴，矩阵，单个信号的采样索引X信号数，类比信号y

       Theta:表示相位谱的纵轴，矩阵，单个信号的采样索引X信号数，类比信号y

main.m（主函数）

%% 信号处理——短时傅里叶变换
%% 作者：冷漠
%% 时间：2024年9月28日
%% 关注公众号 ："故障诊断与寿命预测工具箱",每天进步一点点
clc
clear all
close all
​
% 定义时间向量和啁啾信号参数
fs = 24000; % 采样率
T = 1/fs:1/fs:1; % 1秒长的时间向量
f0 = 100; % 起始频率100Hz
f1 = 5000; % 结束频率5000Hz
​
% 生成啁啾信号
y = chirp(T, f0, 1, f1);
​
% 播放啁啾信号
sound(y, fs);
​
filename = 'chirpSignal.mp3';
% 使用audiowrite函数保存为MP3格式
audiowrite(filename, y, fs, 'Quality', 95);
​
%
[freq1,P1,~]=frequ_am_phase(y',fs);
figure;
subplot(311);plot(T,y,'b-');xlabel('Time/s');ylabel('Amplitude/g');axis tight;
title("啁啾信号的时域波形")
subplot(312);plot(T(1:5000),y(1:5000),'b-');xlabel('Time/s');ylabel('Amplitude/g');axis tight;
title("时域波形的局部细节")
subplot(313);plot(freq1,P1,'b-');xlabel('Frequency/Hz');ylabel('Amplitude/g');
title("啁啾信号的频域波形")
​
​
[s,f,t] = stft(y,fs,Window=rectwin(256),OverlapLength=128,FFTLength=256,FrequencyRange="onesided");
​
​
figure
mesh(t,f,abs(s));colorbar;
xlabel('Time/s');ylabel('Frequency/Hz');zlabel('Amplitude/g');axis tight;
title("matlab的stft函数获得时频图")
​
figure
imagesc(t,f,abs(s));colorbar;
set(gca, 'YDir', 'normal');
xlabel('Time/s');ylabel('Frequency/Hz');axis tight;
title("matlab的stft函数获得时频图")
​
%%  复现短时傅里叶变换结果
rect_win=256;  %矩形窗口的长度
FFT_Length=256;  %FFT分析的长度  
overlap_len=128; %分割信号重叠的长度
seg_counts=floor((length(y)-overlap_len)/(rect_win-overlap_len));
stft_abs=(abs(s));
for i=1:seg_counts
    index=(i-1)*(rect_win-overlap_len)+1:(i-1)*(rect_win-overlap_len)+rect_win;
    sub_y=y(index);
    %复现过程
    Y=fft(sub_y,FFT_Length);          % FFT 快速傅里叶变换
    freq=(0:FFT_Length/2)*fs/FFT_Length;   % 设置频率刻度  横轴Hz
    P2 = abs(Y);
    P1 = P2(1:FFT_Length/2+1)';
    P1(:,3)=stft_abs(:,i);
    y_matrix__man(:,i)=P1(:,1);
end
​
figure;
imagesc(t,freq,y_matrix__man);colorbar;
set(gca, 'YDir', 'normal');
xlabel('Time/s');ylabel('Frequency/Hz');axis tight;
title("手动计算绘制的短时傅里叶变换时频图")
​
fprintf('matlab的stft函数获得时频图与手写复现之间的差为%f \n',sum(stft_abs-y_matrix__man,'all'));

frequ_am_phase.m（幅值谱和相位谱计算函数）

function [freq,P1,Theta]=frequ_am_phase(y,fs,tol)
%% 作者：冷漠
%% 时间：2024年6月01日
%% 关注公众号 ："故障诊断与寿命预测工具箱",每天进步一点点
%% 绘制信号频域的幅值谱和相位谱
%% 参数解释： 
%     y: 表示输入信号，它可以为一个矩阵，行X列,具体为单个信号的采样索引X信号数
%        比如y的大小为8192X12，表示一个有12个信号的数据矩阵，每个信号长度为8192
%        注意，如果仅有一个信号，则y应该是一个列向量
%        同时，y的行数尽量为偶数，奇数的话会引起程序索引的警告
%     fs:表示采样频率
%     tol:相位阈值参数
%     freq:表示幅值谱的横轴
%     P1:表示幅值谱的纵轴
%     Theta:表示相位谱的纵轴
​
if nargin==2
    tol=1e-6;  %计算误差的默认阈值
end
​
L=size(y,1);         % 信号长度
% Y=fft(y,2^nextpow2(L));          % FFT 快速傅里叶变换
Y=fft(y,L);          % FFT 快速傅里叶变换
freq=(0:L/2)*fs/L;   % 设置频率刻度  横轴Hz
%幅值谱
P2 = abs(Y/L);
P1 = P2(1:L/2+1,:);
P1(2:end-1,:) = 2*P1(2:end-1,:);  %纵轴 幅值
​
%相位谱
P2(2:end-1,:)=2*P2(2:end-1,:);
for i=1:size(Y,2)
    Y(P2(:,i)<tol,i) = 0;
    theta(:,i) = angle(Y(:,i))/pi;
end
Theta=theta(1:L/2+1,:);
end

3、细节说明

1、关于啁啾信号的具体公式，不太了解，后续有机会单独出一期讲讲。

2、从复现stft函数来看，它绘制的子信号的FFT的单边频谱的绝对值。

3、本文采用了矩形窗函数，确保了stft和手动计算的一致性。

4、总结

本文模拟了一个啁啾信号，他是一个线性调频信号，并利用短时傅里叶变换分析了它频率的时变特性。同时，复现了matlab的stft函数的计算过程，结果表明复现代码的正确性。

5、相关资料

附件

7en4

1、上述源码

       maintf.m(主函数)；

      frequ_am_phase.m（幅值谱和相位谱计算函数）

    啁啾信号的mp3文件（chirpSignal.mp3）

更多内容，关注公众号“故障诊断与寿命预测工具箱”，每天进步一点点。