局部路径规划算法 - 多项式曲线法
详解了曲线插值法以及代码实现
0 前言
1 多项式曲线法
1.1 算法简介
曲线插值的方法是按照车辆在某些特定条件(安全、快速、高效)下,进行路径的曲线拟合,常见的有多项式曲线、双圆弧段曲线、正弦函数曲线、贝塞尔曲线、B样条曲线等
1.2 算法思想

- 曲线插值法的核心思想就是基于预先构造的曲线类型,根据车辆期望达到的状态(比如要求车辆到达某点的速度和加速度为期望值),将此期望值作为边界条件代入曲线类型进行方程求解,获得曲线的相关系数。
- 曲线所有的相关系数一旦确定,轨迹规划随之完成
2 算法原理
以多项式曲线为例讲解曲线插值法轨迹规划
多项式曲线分为三次,五次,七次多项式曲线
多项式曲线一般而言都是
奇数,这是由边界条件引起的。边界条件一般包括两个点的车辆状态,如换道轨迹起点和终点,因此2倍的车辆状态导致有唯一解的方程系数为偶数。故偶数个系数的多项式也就是奇数多项式。
① 针对三次多项式曲线,最多能确定每一个期望点的两个维度的期望状态,一般来说就是位置和速度。
{
x
(
t
)
=
a
0
+
a
1
t
+
a
2
t
2
+
a
3
t
3
y
(
t
)
=
b
0
+
b
1
t
+
b
2
t
2
+
b
3
t
3
\left\{\begin{array}{l} x(t)=a_{0}+a_{1} t+a_{2} t^{2}+a_{3} t^{3} \\ y(t)=b_{0}+b_{1} t+b_{2} t^{2}+b_{3} t^{3} \end{array}\right.
{x(t)=a0+a1t+a2t2+a3t3y(t)=b0+b1t+b2t2+b3t3
② 针对五次多项式曲线,最多能确定每一个期望点的三个维度的期望状态,一般来说就是位置、速度、加速度。
{
x
(
t
)
=
a
0
+
a
1
t
+
a
2
t
2
+
a
3
t
3
+
a
4
t
4
+
a
5
t
5
y
(
t
)
=
b
0
+
b
1
t
+
b
2
t
2
+
b
3
t
3
+
b
4
t
4
+
b
5
t
5
\left\{\begin{array}{l} x(t)=a_{0}+a_{1} t+a_{2} t^{2}+a_{3} t^{3}+a_{4} t^{4}+a_{5} t^{5} \\ y(t)=b_{0}+b_{1} t+b_{2} t^{2}+b_{3} t^{3}+b_{4} t^{4}+b_{5} t^{5} \end{array}\right.
{x(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5y(t)=b0+b1t+b2t2+b3t3+b4t4+b5t5
③ 针对七次多项式曲线,最多能确定每一个期望点的四个维度的期望状态,一般来说就是位置、速度、加速度、加加速度(冲击度,jerk)。
{
x
(
t
)
=
a
0
+
a
1
t
+
a
2
t
2
+
a
3
t
3
+
a
4
t
4
+
a
5
t
5
+
a
6
t
6
+
a
7
t
7
y
(
t
)
=
b
0
+
b
1
t
+
b
2
t
2
+
b
3
t
3
+
b
4
t
4
+
b
5
t
5
+
b
6
t
6
+
b
7
t
7
\left\{\begin{array}{l} x(t)=a_{0}+a_{1} t+a_{2} t^{2}+a_{3} t^{3}+a_{4} t^{4}+a_{5} t^{5}+a_{6} t^{6}+a_{7} t^{7} \\ y(t)=b_{0}+b_{1} t+b_{2} t^{2}+b_{3} t^{3}+b_{4} t^{4}+b_{5} t^{5}+b_{6} t^{6}+b_{7} t^{7} \end{array}\right.
{x(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5+a6t6+a7t7y(t)=b0+b1t+b2t2+b3t3+b4t4+b5t5+b6t6+b7t7
根据自身轨迹规划的需求,合理选择对应的多项式曲线。
以五次多项式为例:
- 位置
x ( t ) = a 0 + a 1 t + a 2 t 2 + a 3 t 3 + a 4 t 4 + a 5 t 5 y ( t ) = b 0 + b 1 t + b 2 t 2 + b 3 t 3 + b 4 t 4 + b 5 t 5 x(t) = a_{0}+a_{1}t+a_{2}t^2+a_{3}t^3+a_{4}t^4+a_{5}t^5\\ y(t) = b_{0}+b_{1}t+b_{2}t^2+b_{3}t^3+b_{4}t^4+b_{5}t^5 x(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5y(t)=b0+b1t+b2t2+b3t3+b4t4+b5t5 - 速度
x ˙ ( t ) = a 1 + 2 a 2 t + 3 a 3 t 2 + 4 a 4 t 3 + 5 a 5 t 4 y ˙ ( t ) = b 1 + 2 b 2 t + 3 b 3 t 2 + 4 b 4 t 3 + 5 b 5 t 4 \dot{x} (t)=a_{1}+2a_{2}t+3a_{3}t^2+4a_{4}t^3+5a_{5}t^4\\ \dot{y} (t)=b_{1}+2b_{2}t+3b_{3}t^2+4b_{4}t^3+5b_{5}t^4 x˙(t)=a1+2a2t+3a3t2+4a4t3+5a5t4y˙(t)=b1+2b2t+3b3t2+4b4t3+5b5t4 - 加速度
x ¨ ( t ) = 2 a 2 + 6 a 3 t + 12 a 4 t 2 + 20 a 5 t 3 y ¨ ( t ) = 2 b 2 + 6 b 3 t + 12 b 4 t 2 + 20 b 5 t 3 \ddot{x} (t)=2a_{2}+6a_{3}t+12a_{4}t^2+20a_{5}t^3\\ \ddot{y} (t)=2b_{2}+6b_{3}t+12b_{4}t^2+20b_{5}t^3 x¨(t)=2a2+6a3t+12a4t2+20a5t3y¨(t)=2b2+6b3t+12b4t2+20b5t3
化为矩阵形式。
X
=
[
x
(
0
)
x
(
0
)
˙
x
(
0
)
¨
x
(
T
)
x
(
T
)
˙
x
(
T
)
¨
]
=
[
t
0
5
t
0
4
t
0
3
t
0
2
t
0
1
5
t
0
4
4
t
0
3
3
t
0
2
2
t
0
1
0
20
t
0
3
12
t
0
2
6
t
0
2
0
0
t
1
5
t
1
4
t
1
3
t
1
2
t
1
1
5
t
1
4
4
t
1
3
3
t
1
2
2
t
1
1
0
20
t
1
3
12
t
1
2
6
t
1
2
0
0
]
[
a
5
a
4
a
3
a
2
a
1
a
0
]
=
T
X
A
X=\begin{bmatrix}x(0) \\\dot{x(0)} \\\ddot{x(0)} \\x(T) \\\dot{x(T)} \\\ddot{x(T)} \end{bmatrix}=\begin{bmatrix} t_{0}^5& t_{0}^4 & t_{0}^3 & t_{0}^2 & t_{0} &1 \\ 5t_{0}^4 & 4t_{0}^3 & 3t_{0}^2 & 2t_{0} & 1 & 0\\ 20t_{0}^3 & 12t_{0}^2 & 6t_{0} & 2 & 0 & 0\\ t_{1}^5& t_{1}^4 & t_{1}^3 & t_{1}^2 & t_{1}& 1\\ 5t_{1}^4 & 4t_{1}^3 & 3t_{1}^2 & 2t_{1} & 1 & 0\\ 20t_{1}^3 & 12t_{1}^2 & 6t_{1} & 2 & 0 & 0 \end{bmatrix}\begin{bmatrix}a_{5} \\a_{4} \\a_{3} \\a_{2} \\a_{1} \\a_{0} \end{bmatrix}=TXA
X=
x(0)x(0)˙x(0)¨x(T)x(T)˙x(T)¨
=
t055t0420t03t155t1420t13t044t0312t02t144t1312t12t033t026t0t133t126t1t022t02t122t12t010t110100100
a5a4a3a2a1a0
=TXA
Y
=
[
y
(
0
)
y
(
0
)
˙
y
(
0
)
¨
y
(
T
)
y
(
T
)
˙
y
(
T
)
¨
]
=
[
t
0
5
t
0
4
t
0
3
t
0
2
t
0
1
5
t
0
4
4
t
0
3
3
t
0
2
2
t
0
1
0
20
t
0
3
12
t
0
2
6
t
0
2
0
0
t
1
5
t
1
4
t
1
3
t
1
2
t
1
1
5
t
1
4
4
t
1
3
3
t
1
2
2
t
1
1
0
20
t
1
3
12
t
1
2
6
t
1
2
0
0
]
[
a
5
b
4
b
3
b
2
b
1
b
0
]
=
T
X
B
Y=\begin{bmatrix}y(0) \\\dot{y(0)} \\\ddot{y(0)} \\y(T) \\\dot{y(T)} \\\ddot{y(T)} \end{bmatrix}=\begin{bmatrix} t_{0}^5& t_{0}^4 & t_{0}^3 & t_{0}^2 & t_{0} &1 \\ 5t_{0}^4 & 4t_{0}^3 & 3t_{0}^2 & 2t_{0} & 1 & 0\\ 20t_{0}^3 & 12t_{0}^2 & 6t_{0} & 2 & 0 & 0\\ t_{1}^5& t_{1}^4 & t_{1}^3 & t_{1}^2 & t_{1}& 1\\ 5t_{1}^4 & 4t_{1}^3 & 3t_{1}^2 & 2t_{1} & 1 & 0\\ 20t_{1}^3 & 12t_{1}^2 & 6t_{1} & 2 & 0 & 0 \end{bmatrix}\begin{bmatrix}a_{5} \\b_{4} \\b_{3} \\b_{2} \\b_{1} \\b_{0} \end{bmatrix}=TXB
Y=
y(0)y(0)˙y(0)¨y(T)y(T)˙y(T)¨
=
t055t0420t03t155t1420t13t044t0312t02t144t1312t12t033t026t0t133t126t1t022t02t122t12t010t110100100
a5b4b3b2b1b0
=TXB
X
,
Y
,
T
X,Y,T
X,Y,T已知,就可以求出
A
A
A和
B
B
B。
多项式曲线的自变量为时间t,故一旦求解系数矩阵,曲线唯一确定后,则曲线上每一点的导数就代表了车辆经过该点时的速度。这表明多项式曲线换道轨迹规划是路径+速度的耦合结果
五次多项式换道轨迹曲线特指横向位置/纵向位置是关于时间t的五次多项式,而不是指纵向位置y关于横向位置x的五次多项式

- 双圆弧段换道轨迹由弧AC+线段CD+弧DF构成
- 在c点,轨迹曲率由弧AC段的定值
突变为0,故为了让车辆能完全跟随轨迹,考虑到方向盘转角是一个连续缓变过程,车辆行驶到在C点后必须速度为0,让方向盘回正后才能继续行驶,因此无法应用于行车路径规划,而应用于泊车路径规划。
MATLAB(Ally)
clc
clear
close all
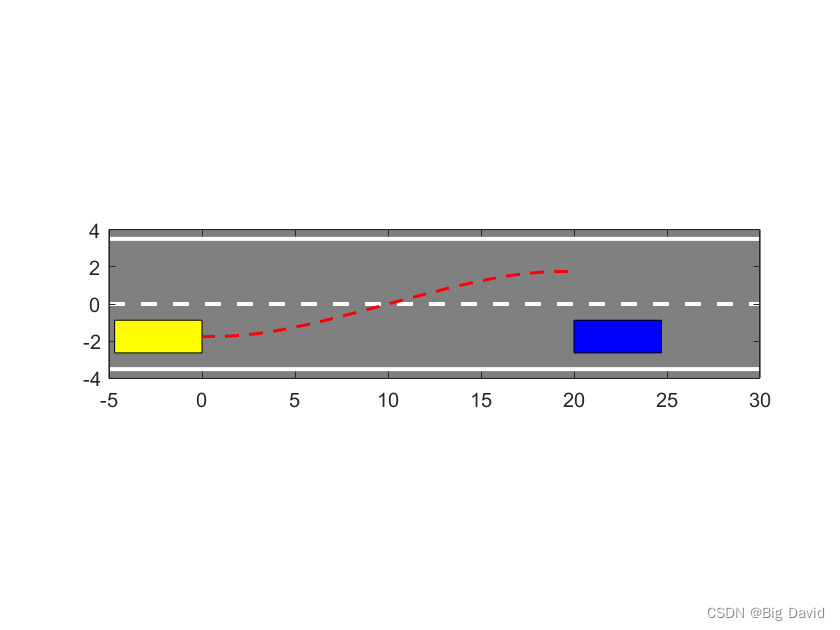
%% 场景定义
% 换道场景路段与车辆相关参数的定义
d = 3.5; % 道路标准宽度
len_line = 30; % 直线段长度
W = 1.75; % 车宽
L = 4.7; % 车长
x1 = 20; %1号车x坐标
% 车辆换道初始状态与终点期望状态
t0 = 0;
t1 = 3;
state_t0 = [0, -d/2; 5, 0; 0, 0]; % x,y; vx,vy; ax,ay
state_t1 = [20, d/2; 5, 0; 0, 0];
x2 = state_t0(1);
%% 画场景示意图
figure(1)
% 画灰色路面图
GreyZone = [-5,-d-0.5; -5,d+0.5; len_line,d+0.5; len_line,-d-0.5];
fill(GreyZone(:,1),GreyZone(:,2),[0.5 0.5 0.5]);
hold on
% 画小车
fill([x1,x1,x1+L,x1+L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'b') %1号车
fill([x2,x2,x2-L,x2-L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'y') %2号车
% 画分界线
plot([-5, len_line],[0, 0], 'w--', 'linewidth',2); %分界线
plot([-5,len_line],[d,d],'w','linewidth',2); %左边界线
plot([-5,len_line],[-d,-d],'w','linewidth',2); %左边界线
% 设置坐标轴显示范围
axis equal
set(gca, 'XLim',[-5 len_line]);
set(gca, 'YLim',[-4 4]);
%% 五次多项式轨迹生成
% 计算A和B两个系数矩阵
X = [state_t0(:,1); state_t1(:,1)];
Y = [state_t0(:,2); state_t1(:,2)];
T = [ t0^5 t0^4 t0^3 t0^2 t0 1;
5*t0^4 4*t0^3 3*t0^2 2*t0 1 0;
20*t0^3 12*t0^2 6*t0 1 0 0;
t1^5 t1^4 t1^3 t1^2 t1 1;
5*t1^4 4*t1^3 3*t1^2 2*t1 1 0;
20*t1^3 12*t1^2 6*t1 1 0 0];
A = T \ X;
B = T \ Y;
% 将时间从t0到t1离散化,获得离散时刻的轨迹坐标
t=(t0:0.05:t1)';
path=zeros(length(t),4);%1-4列分别存放x,y,vx,vy
for i = 1:length(t)
% 纵向位置坐标
path(i,1) = [t(i)^5, t(i)^4, t(i)^3, t(i)^2, t(i), 1] * A;
% 横向位置坐标
path(i,2) = [t(i)^5, t(i)^4, t(i)^3, t(i)^2, t(i), 1] * B;
% 纵向速度
path(i,3) = [5*t(i)^4, 4*t(i)^3, 3*t(i)^2, 2*t(i), 1, 0] * A;
% 横向速度
path(i,4) = [5*t(i)^4, 4*t(i)^3, 3*t(i)^2, 2*t(i), 1, 0] * B;
end
% 画换道轨迹
plot(path(:,1),path(:,2),'r--','linewidth',1.5);
%% 分析速度
% 横向速度
figure
plot(t, path(:,4), 'k');
xlabel('时间 / s ');
ylabel('横向速度 / m/s ');
% 纵向速度
figure
plot(t, path(:,3), 'k');
xlabel('时间 / s ');
ylabel('纵向速度 / m/s ');
运行结果:



C++:
//
// Created by bigdavid on 2024/3/18.
//
#include <iostream>
#include <Eigen/Dense>
#include <vector>
#include "../include/matplotlibcpp.h"
namespace plt = matplotlibcpp;
using namespace std;
using namespace Eigen;
int main(int argc, char** argv) {
double d = 3.5; //道路标准宽度
double len_line = 30; //直线段长度
double W=1.60; //车宽
double L=3.275; //车长
// 车辆换道初始状态与终点期望状态
double t0 = 0, t1 = 5;
VectorXd state_t0(6), state_t1(6);
state_t0 << 0, -d/2, 5, 0, 0, 0;
state_t1 << 20, d/2, 5, 0, 0, 0;
// 把起末两点的横纵向方程统一用矩阵表达
VectorXd X(6),Y(6);
X << state_t0[0],state_t0[2],state_t0[4],state_t1[0],state_t1[2],state_t1[4];
Y << state_t0[1],state_t0[3],state_t0[5],state_t1[1],state_t1[3],state_t1[5];
MatrixXd T(6,6);
T << pow(t0, 5),pow(t0, 4),pow(t0, 3),pow(t0, 2),t0,1,
5*pow(t0,4),4*pow(t0,3),3*pow(t0,2),2*t0,1,0,
20*pow(t0,3),12*pow(t0,3),6*t0,1,0,0,
pow(t1, 5),pow(t1, 4),pow(t1, 3),pow(t1, 2),t1,1,
5*pow(t1,4),4*pow(t1,3),3*pow(t1,2),2*t1,1,0,
20*pow(t1,3),12*pow(t1,3),6*t1,1,0,0;
// 计算A B
MatrixXd A = T.inverse() * X;
MatrixXd B = T.inverse() * Y;
vector<double> x_, y_, v_x, v_y;
vector<double> time;
int cnt = 0;
for(double t = t0; t < t1 + 0.05;t += 0.05) {
cnt++;
time.push_back(t);
}
MatrixXd temp1(1,6), temp2(1,6);
for(int i = 0; i < cnt; i++){
temp1 << pow(time[i], 5),pow(time[i], 4),pow(time[i], 3),pow(time[i], 2),time[i],1;
x_.push_back((temp1 * A)(0,0));
y_.push_back((temp1 * B)(0,0));
temp2 << 5 * pow(time[i],4), 4 * pow(time[i],3), 3 * pow(time[i],2),2 * time[i],1,0;
v_x.push_back((temp2 * A)(0,0));
v_y.push_back((temp2 * B)(0,0));
}
//画图
plt::figure(1);
plt::plot(x_, y_,"r");
// 横向速度
plt::figure(2);
plt::plot(time, v_x);
// 纵向速度
plt::figure(3);
plt::plot(time, v_y);
// save figure
const char* filename = "./curve_demo.png";
plt::save(filename);
plt::show();
return 0;
}
运行结果:




开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容





所有评论(0)