LSTM输出门,遗忘门,输入门详细介绍以及代码实现
在学习正确解标签时,重要的是RNN层的存在,RNN层通过向过去传递有意义的梯度,能够学习时间方向上的依赖关系,此时梯度,包含哪些应该学习到有意义的信息,通过将这些信息向过去传递,RNN层学习长期的依赖关系,但是,如果这个梯度在中途变弱,则权重参数将不会被更新,也就是说,RNN层无法学习长期的依赖关系,
在学习正确解标签时,重要的是RNN层的存在,RNN层通过向过去传递有意义的梯度,能够学习时间方向上的依赖关系,此时梯度,包含哪些应该学习到有意义的信息,通过将这些信息向过去传递,RNN层学习长期的依赖关系,但是,如果这个梯度在中途变弱,则权重参数将不会被更新,也就是说,RNN层无法学习长期的依赖关系,
梯度消失和梯度爆炸的原因
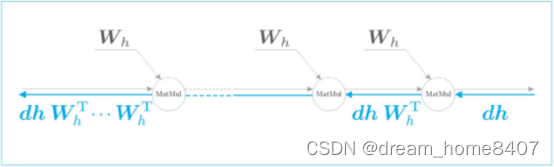
这里我们关注RNN层在时间方向上的梯度传播,这里考虑长度为T的时序数据,关注从第T个正解标签传递出梯度如何变化,就上面的问题来说,这相当第T个正解标签是Tom的情形,此时关注时间方向上的梯度,可知反向传播的梯度流经tanh,”+”,和Matmul(矩阵乘积)运算。
‘+’的反向传播将上游传来的梯度原样传递给下游,因此梯度的值不变,那么
剩下的tanh和MatMul运算会发生怎样变化,

总结来说,随着学习越来越长依赖关系,梯度大小随着步长呈指数级减小,这就是梯度消失,梯度消消失发生后,梯度将迅速变小,权重梯度将不能更新,模型就无法学习长依赖关系,
梯度为什么会出现指数级增加或者减小呢,因为权重矩阵Wh被反复乘了T次,如果Wh大于1,梯度呈指数级增加,当Wh小于1,梯度呈指数级减小,
梯度爆炸的对策
有一个简单解决梯度爆炸的方法,是梯度裁剪,设置阈值,如果梯度的L2范数大于或者等于阈值,就进行梯度修正,这就是梯度裁剪
LSTM
RNN简略图

LSTM简略图

RNN层与LSTM层的比较
LSTM与RNN的接口不用指出在于,LSTM还有路径C,这个C称为记忆单元,相当于LSTM专用记忆部门,
记忆单元的特点是,仅在LSTM层内部接收和传递数据,也就是说,记忆单元在LSTM层内部结束,不向其他层传输,而LSTM的隐藏状态H和RNN层相同,会被向上传递到其他层,
LSTM层的结构
现在我们看一下LSTM层的内部结构,如前所述,LSTM有记忆单元Ct,这个Ct存储了时刻t时LSTM的记忆,可以认为t其中保存了从过去到时刻t的所有必要信息,然后基于这个充满必要信息的记忆,向外部的层(和下一个时刻的LSTM)输出隐藏状态ht

LSTM层基于记忆单元Ct计算隐藏状态ht,当前记忆单元Ct,如上图所示,当前的记忆单元Ct是基于3个输入Ct-1,ht-1,和xt,经过某种计算算出来,这里的重点是隐藏状态ht要用更新后的ct来计算,记忆单元ct和隐藏状态ht的关系只是按元素应用tanh函数,这就意味着,记忆单元ct和隐藏状态ht的元素个数相同,
接下来介绍门的概念,在这里是控制数据的流动,LSTM中使用的门并非只能控制开或者合,还可以控制开合程度,类似控制水流一样,
有专门的权重参数控制门的开合程度,这些权重参数通过学习被更新,另外,sigmoid函数用于求门的开合程度
输出门
现在我们将话题LSTM,刚才说明了,隐藏状态ht对记忆单元ct仅仅用来tanh函数,这里考虑对tanh施加门,换句话来说,针对tanh的各个元素,调整它们下一时刻的隐藏状态的重要程度,由于这个门管理下一个隐藏状态ht的输出,说一称之为输出门,
输出门的开合程度(流出比例),根据输入xt和上一个状态ht-1求出,此时进行计算如下图,这里在使用权重参数和偏置的上标上方添加output的首字母o,之后,我们也将使用上标表示门,另外sigmoid函数用Q()表示

输入xt有权重wx,上一时刻的状态ht-1有权重wh,将它们的矩阵乘积和偏置b之和传给sigmoid函数,最后就是输出们的输出o,最后,将这个o和tanh(ct)的对应元素的乘积作为ht输出,将这些计算绘制成计算图如下:

将输出门进行计算表示为sigma,然后,将它的输出表示为o,则ht可由o和tanh(ct)的乘积计算出来,这里说的乘积是对应元素的乘积,
以上就是lstm的输出门,这样一来,lstm的输出部分就完成了,接着我们再来看一下记忆单元的更新部分
Tanh的输出是-0.11.0之间的实数,我们可以认为这个-1.01.0的数值表示某种被编码的信息强弱,而sigmoid的输出是0~1之间的实数,表示数据流出的比例,因此,大多数情况下,门使用sigmoid函数作为激活函数,而包含实质信息的数据则使用tanh函数作为激活函数,
遗忘门
遗忘门确定要忘记什么,我们在ct-1上添加一个忘记不必要记忆的门,将遗忘门添加到LSTM中,如图

将遗忘门进行的一系列计算表示为Q,其中有遗忘门专用的权重参数,此时的计算如下:

遗忘门的输出f可以由上式得到,然后ct由这个f和上一个记忆单元ct-1的对应元素的乘积求得
遗忘门从上一个时刻的记忆单元中删除了应该忘记的东西,但是这样的化,记忆单元只会忘记信息,现在我们还想向这个记忆单元添加一些应当记住的信息,为此我们添加新的tanh节点

基于tanh节点计算的结果被加到上一时刻的记忆单元ct-1上,新的信息就被添加到记忆单元中,这个tanh节点的作用不是门,而是将新的信息添加到基于单元中

这里用g表示向记忆单元添加新的信息,通过将这个g
加到上一个时刻ct-1上,形成新的记忆
输出门
最后,给g添加门,这里将新添加的门称之为输入门,添加输入门后,计算图如下

输入门判断新增信息g的各元素价值有多大,输入门不会不经考虑就添加新信息,而是会对要添加的信息进行取舍,换句话来说,输入门会添加加权后的新信息,

然后,将i和g的对应元素的乘积添加到记忆单元中,以上就是对LSTM的内部处理说明
总结LSTM由三路输入组成,当前输入时序数据xt,RNN层输出ht(也称之为隐藏状态,它记录过去的信息),和记忆单元c,记忆单元在LSTM层内部结束工作,不向其他层输出,这里记忆着从开始到此刻必要信息,
其中包含输出门,遗忘门,输入门,用到的重要函数是tanh和sigmoid,tan’h控制重要信息输出多少,sigmoid控制门开合程度
LSTM的梯度的流动

我门记录记忆单元的反向传播,记忆单元的反向传播仅流过“+”和“”节点,‘+’节点将上游传过来的梯度原样流出,所以梯度没有变化,而‘’节点的计算并不是矩阵乘积,而是对应元素乘积,RNN的反向传播进行,使用相同权重矩阵重复多次矩阵乘积计算,由此导致了梯度消失,这里的LSTM的反向传播进行的不是矩阵乘积计算,而是对应元素的层级计算,每次都会基于不同的门对乘积进行计算,
‘*’节点的计算由遗忘门控制,遗忘门认为应该忘记的元素,其梯度会变小,而遗忘门认为不能忘记的元素,其梯度在向过去的方向流动时不会退化,因此,记忆单元的梯度能在不发生梯度消失的情况下传播,
使用LSTM的语言模型

叠加两个 LSTM 层的例子。此时,第一个 LSTM 层的隐藏状态是第两个 LSTM 层的输入。按照同样的方式,我们可以叠加多个 LSTM层,从而学习更加复杂的模式,这和前馈神经网络时的层加深是一样的。
那么,应该叠加几个层呢?这其实是一个关于超参数的问题。因为层数是超
参数,所以需要根据要解决的问题的复杂程度、能给到的训练数据的规模来
确定。顺便说一句,在 PTB 数据集上学习语言模型的情况下,当 LSTM 的
层数为 2 ~ 4 时,可以获得比较好的结果。
代码实现
class TimeLSTM:
def __init__(self, Wx, Wh, b, stateful=False):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx),
np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None
self.h, self.c = None, None
self.dh = None
self.stateful = stateful
def forward(self, xs):
Wx, Wh, b = self.params
N, T, D = xs.shape
H = Wh.shape[0]
self.layers = []
hs = np.empty((N, T, H), dtype='f')
if not self.stateful or self.h is None:
self.h = np.zeros((N, H), dtype='f')
if not self.stateful or self.c is None:
self.c = np.zeros((N, H), dtype='f')
for t in range(T):
layer = LSTM(*self.params)
self.h, self.c = layer.forward(xs[:, t, :],
self.h, self.c)
hs[:, t, :] = self.h
self.layers.append(layer)
return hs
def backward(self, dhs):
Wx, Wh, b = self.params
N, T, H = dhs.shape
D = Wx.shape[0]
dxs = np.empty((N, T, D), dtype='f')
dh, dc = 0, 0
grads = [0, 0, 0]
for t in reversed(range(T)):
layer = self.layers[t]
dx, dh, dc = layer.backward(dhs[:, t, :] +
dh, dc)
dxs[:, t, :] = dx
for i, grad in enumerate(layer.grads):
grads[i] += grad
for i, grad in enumerate(grads):
self.grads[i][...] = grad
self.dh = dh
return dxs
def set_state(self, h, c=None):
self.h, self.c = h, c
def reset_state(self):
self.h, self.c = None, None
基于dropout抑制过拟合
通过叠加LSTM层,可以期待能够学习到时序数据的复杂依赖关系,换句话来说,通过加深层,可以创建表现力更强的模型,但是这样的模型往往更容易过拟合,过拟合是指学习了训练数据的状态,也就是说,过拟合是一种缺乏泛化能力的状态,我们想要的是一个泛化能力强的模型,因此必须基于训练数据和验证数据的评价差异,判断是否过拟合,并依据此来进行模型设计,
抑制过拟合已有既定的方法,一是丰富训练数据特征:二是降低模型的复杂程度,
我们会优先考虑这两个方法。除此之外,对模型复杂度给予惩罚的正则化也
很有效。比如,L2 正则化会对过大的权重进行惩罚。
此外,像 Dropout[9] 这样,在训练时随机忽略层的一部分(比如 50 %)神
经元,也可以被视为一种正则化(图 6-30)。本节我们将仔细研究
Dropout,并将其应用于 RNN
Dropout随机选择一部分神经元,然后忽略它们,停止向前传递信号,这种随机忽视是 一种制约,可以提高神经元的泛化能力,卷积神经网络使用的地方是在激活函数后面插入dropout层,那语言模型应该放在哪里

在深度方向(垂直方向)上插入 Dropout 层
这样一来,无论沿时间方向(水平方向)前进多少,信息都不会丢失。
Dropout 与时间轴独立,仅在深度方向(垂直方向)上起作用。

权值共享
改进语言模型由一个非常简单的技巧是权值共享

语言模型中共享权重的例子:Embedding 层和 Softmax 前的Affine 层共享权重
共享Embedding和Affine层权重的技巧在于权重共享,通过两个层之间共享权重,可以大大减少学习的参数数量,
如何实现,假设词汇量为v,lstm隐藏状态维度是H,则embedding层的权重形状为vh,affine层的权重形状是hv,此时,如果权重共享,只需要将Embedding层权重转置设置为Affine层的权重,这个简单的技巧可以带来出色的结果,
为什么说权重共享是有效的呢?直
观上,共享权重可以减少需要学习的参数数量,从而促进学习。另外,
参数数量减少,还能收获抑制过拟合的好处。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)