首先回顾一下整个GNN的结构，前面我们所介绍的都是红色框内所解决的任务。

最终得到的节点嵌入结果，是一个关于每个在$L$层节点嵌入的集合：

$$\left\{{\mathbf{h}}_v^{(L)},\forall v\in G\right\}$$

下面来我们来介绍图网络里，蓝色框中的预测任务（prediction head），其中包括：节点水平、边水平、图水平的三种预测：

---

① 节点水平预测

节点水平的预测我们可以直接采用最终的嵌入结果。也可以再进行一个线性变换最终得到所需要的结果。这里假设在经过 GNN 的计算后，我们可以得到一个 $d$ 维的嵌入向量：$\left\{{\mathbf{h}}_v^{(L)}\in {\mathbb{R}}^d,\forall v\in G\right\}$。

假设我们需要的实际结果是 $k$ 个目标的（可以为 $k$ 维的分类问题；或者是 $k$ 个目标的回归问题），那么最终的预测结果如下：

$${\hat{y}}_v={\mathrm{Head}}_{\text{node }}\left({\mathbf{h}}_v^{(L)}\right)={\mathbf{W}}^{(H)}{\mathbf{h}}_v^{(L)}$$

其中 ${\mathbf{W}}^{(H)}\in {\mathbb{R}}^{k\ast d}$，为权重矩阵。

---

② 边水平预测

假设边水平的预测也同样需要输出$k$个预测结果，需要预测$u,v$两个节点之间的边嵌入结果。

预测公式如下：

$${\hat{\mathbf{y}}}_{uv}={\mathrm{Head}}_{\text{edge }}\left({\mathbf{h}}_u^{(L)},{\mathbf{h}}_v^{(L)}\right)$$

• 方式一：拼接+线性变换

这种方式之前在 attention 机制中出现过：

具体操作方式是先拼接，再进行线性变换。

$${\hat{\mathbf{y}}}_{uv}=\mathrm{Linear}\left(\mathrm{Concat}\left({\mathbf{h}}_u^{(L)},{\mathbf{h}}_v^{(L)}\right)\right)$$

• 方式二：内积

要求输出的边嵌入为一维时，可以直接通过如下内积方式得到：

$${\hat{y}}_{uv}={\left({\mathbf{h}}_u^{(L)}\right)}^T{\mathbf{h}}_v^{(L)}$$

要求为$k$维时，参考多头注意力机制，构建一系列可训练的权重矩阵：${\mathbf{W}}^{(1)},\dots ,{\mathbf{W}}^{(k)}$。具体$k$个维度的构造如下：

$$\begin{array}{c}{\hat{y}}_{uv}^{(1)}={\left({\mathbf{h}}_u^{(L)}\right)}^T{\mathbf{W}}^{(1)}{\mathbf{h}}_v^{(L)}\\ {\hat{y}}_{uv}^{(k)}={\left({\mathbf{h}}_u^{(L)}\right)}^T{\mathbf{W}}^{(k)}{\mathbf{h}}_v^{(L)}\\ {\hat{\mathbf{y}}}_{uv}=\mathrm{Concat}\left({\hat{y}}_{uv}^{(1)},\dots ,{\hat{y}}_{uv}^{(k)}\right)\in {\mathbb{R}}^k\end{array}$$

---

③ 图水平预测

图水平的预测其实非常类似GNN中的聚合操作：

$${\hat{\mathbf{y}}}_G=\mathrm{AGG}\left(\left\{{\mathbf{h}}_v^{(L)}\in {\mathbb{R}}^d,\forall v\in G\right\}\right)$$

其中的 $\mathrm{AGG}$ 可以为 $\mathrm{Mean},\mathrm{Max},\mathrm{Sum}$ 等。

但这样的嵌入可能会损失一些信息，特别是针对一些比较大的图结构时。例如两个完全不同的图，节点嵌入分别为：
G 1 : { − 1 , − 2 , 0 , 1 , 2 } G_{1}:\{-1,-2,0,1,2\} G1​:{−1,−2,0,1,2}
G 2 : { − 10 , − 20 , 0 , 10 , 20 } G_{2}:\{-10,-20,0,10,20\} G2​:{−10,−20,0,10,20}

如果聚合函数选择为$\mathrm{Sum}$时，图嵌入为：
G 1 : y ^ G = Sum ⁡ ( { − 1 , − 2 , 0 , 1 , 2 } ) = 0 G_{1}: \hat{y}_{G}=\operatorname{Sum}(\{-1,-2,0,1,2\})=0 G1​:y^​G​=Sum({−1,−2,0,1,2})=0
G 2 : y ^ G = Sum ⁡ ( { − 10 , − 20 , 0 , 10 , 20 } ) = 0 G_{2}: \hat{y}_{G}=\operatorname{Sum}(\{-10,-20,0,10,20\})=0 G2​:y^​G​=Sum({−10,−20,0,10,20})=0

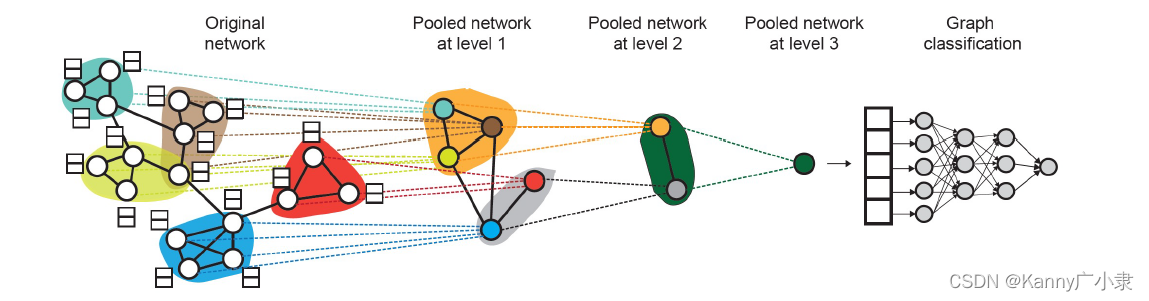
两者结果完全一致。因此我们考虑一种层级全局池化方法（hierarchical global pooling），进行聚合操作，得到最终的图嵌入。

我们的GNN网络分别用于两种操作，第一种就是前面介绍的节点嵌入。第二种就是构建一个聚类网络，对原始网络中的每个节点进行聚类，而后在根据层级聚类结果进行一层一层的池化聚合操作，最终得到我们需要的整个图的嵌入结果。整个流程如下：

以前面的方法举例，假设我们根据 $G_1,G_2$ 由五个节点组成的图最终被聚成了两类（前两个节点一类，后两个节点一类），那么我们逐层进行聚合：

• $G_1$ 的节点嵌入： { − 1 , − 2 , 0 , 1 , 2 } \{-1,-2,0,1,2\} {−1,−2,0,1,2}
   第一轮： y ^ a = ReLU ⁡ ( Sum ⁡ ( { − 1 , − 2 } ) ) = 0 , y ^ b = ReLU ⁡ ( Sum ⁡ ( { 0 , 1 , 2 } ) ) = 3  第二轮： y ^ G = ReLU ⁡ ( Sum ⁡ ( { y a , y b } ) ) = 3 \begin{aligned} &\text { 第一轮：} \hat{y}_{a}=\operatorname{ReLU}(\operatorname{Sum}(\{-1,-2\}))=0, \quad \hat{y}_{b}= \operatorname{ReLU}(\operatorname{Sum}(\{0,1,2\}))=3 \\ &\text { 第二轮：} \hat{y}_{G}=\operatorname{ReLU}\left(\operatorname{Sum}\left(\left\{y_{a}, y_{b}\right\}\right)\right)=3 \end{aligned} ​ 第一轮：y^​a​=ReLU(Sum({−1,−2}))=0,y^​b​=ReLU(Sum({0,1,2}))=3 第二轮：y^​G​=ReLU(Sum({ya​,yb​}))=3​

• $G_2$ 的节点嵌入： { − 10 , − 20 , 0 , 10 , 20 } \{-10,-20,0,10,20\} {−10,−20,0,10,20}
   第一轮： y ^ a = ReLU ⁡ ( Sum ⁡ ( { − 10 , − 20 } ) ) = 0 , y ^ b = ReLU ⁡ ( Sum ⁡ ( { 0 , 10 , 20 } ) ) = 30  第二轮： y ^ G = ReLU ⁡ ( Sum ⁡ ( { y a , y b } ) ) = 30 \begin{aligned} &\text { 第一轮：} \hat{y}_{a}=\operatorname{ReLU}(\operatorname{Sum}(\{-10,-20\}))=0, \quad \hat{y}_{b}= \operatorname{ReLU}(\operatorname{Sum}(\{0,10,20\}))=30 \\ &\text { 第二轮：} \hat{y}_{G}=\operatorname{ReLU}\left(\operatorname{Sum}\left(\left\{y_{a}, y_{b}\right\}\right)\right)=30 \end{aligned} ​ 第一轮：y^​a​=ReLU(Sum({−10,−20}))=0,y^​b​=ReLU(Sum({0,10,20}))=30 第二轮：y^​G​=ReLU(Sum({ya​,yb​}))=30​

两个图会得到不一样的结果，因此这种方式是能够有效区分这种情形。