（本人蒟蒻，如有不足，望各位大佬不吝指出）

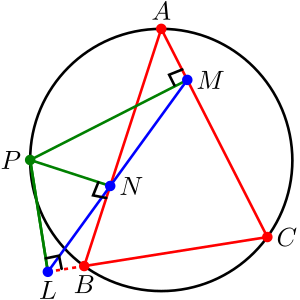
定理简介——西姆松定理

有 $△ABC$ ，平面上有一点 $P$ 。$P$ 在三角形三边上的投影（即由 $P$ 到边上的垂足）共线（此线称为

西姆松线Simson line）当且仅当 $P$ 在三角形 $△ABC$ 的外接圆上。如图，即 $L,N,M$ 共线：

---

证法1：平角

如图，证明 $\angle DFE+\angle DFG=180°$ ，

可知 $D,B,C,A$ 四点共圆，所以 $\angle DBE=\angle DAC$，

因为 $\angle DEB=\angle DFB=90°$ ，所以 $D,E,B,F$ 四点共圆，所以 $\angle DBE=\angle DFE$，

因为 $\angle DFA=\angle DGA=90°$ ，所以$D,F,G,A$ 四点共圆，所以 $\angle DFG+\angle DAC=180°$，

即 $\angle DFE+\angle DFG=180°$，得证。

---

证法2：重合

2-1

延长 $GF$ 交 $CB$ 延长线于 $E^{\prime }$，证明 $E,E^{\prime }$ 重合。

$D,F,G,A$ 四点共圆，则 $\angle DF{E}^{\prime }=\angle DAC$，

$D,B,C,A$ 四点共圆，则 $\angle DBE=\angle DAC$，

$D,E,B,F$ 四点共圆，则 $\angle DBE=\angle DFE$，

故 $\angle DFE=\angle DF{E}^{\prime }$，则 $E,E^{\prime }$ 重合，得证。

2-2

证明 $EF,EG$重合，可证明 $\angle DEF=\angle DEG$。

$D,E,B,F$ 四点共圆，则 $\angle DEF=\angle DBF$，

$D,B,C,A$ 四点共圆，则 $\angle DBF=\angle DCA$，

$D,E,C,G$ 四点共圆，则 $\angle DEG=\angle DCA$，

故 $\angle DEF=\angle DEG$，得证。

---

证法3：对顶角

证明 $\angle EFB=\angle AFG$，则 $E,F,G$ 共线。

$D,F,G,A$ 四点共圆，则 $\angle AFG=\angle ADG$，

$D,F,B,E$ 四点共圆，则 $\angle EFB=\angle EDB$，

$D,B,C,A$ 四点共圆，则 $\angle DBE=\angle DAC$，余角 $EDB=\angle ADG$，

故 $\angle EFB=\angle AFG$，得证。

---

证法4：梅涅劳斯定理的逆定理

即证明：$\frac{AF}{FB}\cdot \frac{BE}{EC}\cdot \frac{CG}{GA}=1$

由四点共圆可以得到上图中颜色相同的角相等，此处便不再赘述，则

$△ADF\sim △CDE\Rightarrow \frac{AF}{EC}=\frac{AD}{DC}$

$△DEB\sim △DGA\Rightarrow \frac{BE}{GA}=\frac{BD}{AD}$

$△CDG\sim △DBF\Rightarrow \frac{CG}{FB}=\frac{DC}{BD}$

$\therefore \frac{AF}{FB}\cdot \frac{BE}{EC}\cdot \frac{CG}{GA}=\frac{AD}{DC}\cdot \frac{BD}{AD}\cdot \frac{DC}{BD}=1$，得证。

---

拓展——斯坦纳定理

简介

即，西姆松线经过 $△ABC$ 的垂心与点 $D$ 连成的线段的中点，如图，红线（即西姆松线）经过蓝线的

中点：

---

证法1：全等三角形

引理1

引理： 三角形垂心关于一边的对成点在三角形的外接圆上。

证明： 如图，$G$ 为 $△ABC$ 的垂心，延长 $GD$ 交 $△ABC$ 的外接圆与 $H$ ，则

$\angle ABC=\angle DGC=90°-\angle GCD$，

又有 $A,B,H,C$ 四点共圆，则 $\angle ABC=\angle CHD$，

所以 $△CGD≌△CHD(\mathrm{A}\mathrm{A}\mathrm{S})$，即三角形垂心关于一边的对成点在三角形的外接圆上，得证。

定理证明

如图，连接 $CK$ 并延长交西姆松线 $EG$ 于 $P$ ，交 $AB$ 于 $O$ ，交 $△ABC$ 的外接圆于 $M$，

过 $D$ 作 $DN\perp OM$ 于 $N$ ，连接 $AD$，

证明 $△DFL≌△KPL$ 即可。

由对顶角有 $\angle DLF=\angle KLP$，

由垂心的定义可知 $PK//DF$，则有 $\angle FDL=\angle PKL$，

下证 $DF=PK$。

易知四边形$NDFO$为矩形，故可证 $ON=PK$，

由上面的引理1可知 $OM=OK$ ，故证明 $MN=OP$ 即可。

由 $D,F,G,A$ 四点共圆，有 $\angle OPF=\angle ADG$，

由 $M,D,C,A$ 四点共圆，有 $\angle DMN=\angle DAG$，余角 $\angle MDN=\angle ADG$

所以 $\angle MDN=\angle OPF$。

四边形$NDFO$为矩形，则 $DN=OF$，

所以 $△MDN≌△PFO(\mathrm{A}\mathrm{S}\mathrm{A})$，$MN=OP$，

故可推出 $DF=PK$，所以 $△DFL≌△KPL(\mathrm{A}\mathrm{A}\mathrm{S})$，$DL=KL$，得证。

---

证法2：中位线1

该方法与证法1大体相似，同样也需要用到上面证明的引理1。

如图，连接 $CK$ 并延长交西姆松线 $EG$ 于 $P$ ，交 $AB$ 于 $O$ ，交 $△ABC$ 的外接圆于 $M$，

作 $D$ 关于 $AB$ 的对称点 $D^{\prime }$，连接 $DK$，证明 $FL$ 是 $△D{D}^{\prime }K$ 的中位线。

由于 $D$ 与 $D^{\prime }$ 关于 $AB$ 对称即 $F$ 为 $D{D}^{\prime }$ 中点，则证明 $FL//D^{\prime }K$ 即可。

由于 $M$ 与 $K$，$D$ 与 $D^{\prime }$ 关于 $AB$ 对称，则四边形$MD{D}^{\prime }K$为等腰梯形，

故 $\angle DMO=\angle D^{\prime }KO$ 。

由 $M,D,A,C$ 四点共圆，有 $\angle DMO=\angle DAC$，

由 $D,F,G,A$ 四点共圆，有 $\angle OFP=\angle ADG$，余角 $\angle OPF=\angle DAC$，

故 $\angle D^{\prime }KO=\angle OPF$，$Fl//D^{\prime }K$，$FL$ 为$△D{D}^{\prime }K$ 的中位线，$DL=KL$，得证。

---

证法3：三角恒等变换

引理2

如图：设$\angle ABC=\beta ,\angle ACB=\gamma$，则 $GD=2R\cdot \mathrm{c}\mathrm{o}\mathrm{s}\beta \mathrm{c}\mathrm{o}\mathrm{s}\gamma$。

证明：

$I$ 为圆心，$AJ$ 为直径，连接 $JB,JC,HB,HC$。

由前面的性质可知 $△CDG≌△CHD$，则 $GD=DH,\angle GCD=\angle HCD$。

又有 $\angle ABJ=90°=\angle BFC$，则 $BJ//FC$，则 $\angle GCD=\angle JBC$。

故 $\angle JBC=\angle HCD$。

$D,J,H,C$ 四点共圆，有 $\angle BJC=\angle BHC$，

则 $△BJC≌△CHB(\mathrm{A}\mathrm{A}\mathrm{S})$，$CJ=BH$。

$B,J,C,A$ 四点共圆，有 $\angle AJC=\angle ABC=\beta$，

故 $2R\cdot \mathrm{c}\mathrm{o}\mathrm{s}\beta =CJ=BH$，

$B,H,C,A$ 四点共圆，有 $\angle BHD=\angle ACB=\gamma$，

故 $2R\cdot \mathrm{c}\mathrm{o}\mathrm{s}\beta \mathrm{c}\mathrm{o}\mathrm{s}\gamma =BH\cdot \cos \gamma =DH=GD$，得证。

同时，全等可以得到 $JH//BC$，在下文的引理3中会用到。

定理证明

如图，连接 $CK$ 并延长交西姆松线 $EG$ 于 $P$ ，交 $AB$ 于 $O$ ，交 $△ABC$ 的外接圆于 $M$，

连接 $CD,AD$。

思路类似证法1，证明 $DF=PK$，证明全等。

$DF$ 容易求出，而 $PK$ 可由 $OK-OP$ 得到，

$OK$ 可以用上面的引理2求出，$OP$ 则可在 $△OPF$ 中求得。

设 $\angle BAC=\alpha ,\angle ABC=\beta ,\angle ACB=\gamma ,\angle DAB=\theta$，

$A,D,B,C$ 四点共圆，则 $\angle DCB=\angle DAB=\theta$，

在 $△ADC$ 中，由正弦定理有 $AD=2R\cdot \sin (\gamma -\theta )$，

故 $DF=AD\cdot \sin \theta =2R\cdot \sin (\gamma -\theta )\sin \theta$，

$AF=AD\cdot \cos \theta =2R\cdot \sin (\gamma -\theta )\cos \theta =R(\cos (\gamma -2\theta )-\cos \gamma )$，

$AO=AC\cdot \cos \alpha$，由正弦定理有 $AC=2R\cdot \sin \beta$，故 $AO=2R\cdot \sin \beta \cos \alpha$，

所以 $OF=AF-AO=2R\cdot \sin (\gamma -\theta )\cos \theta -2R\cdot \sin \beta \cos \alpha$，

积化和差，$OF=R(\sin \gamma +sin(\gamma -2\theta )-\sin (\alpha +\beta )-\sin (\beta -\alpha ))$，

又 $\alpha +\beta +\gamma =\pi$，则 $\sin \gamma =\sin (\alpha +\beta )$，

所以，$OF=R(\sin (\gamma -2\theta )-\sin (\beta -\alpha ))=R(\sin ((\pi -\alpha -\beta )-2\theta )-\sin (\beta -\alpha ))$，

即，$OF=R(\sin (\pi -(\alpha +\beta +2\theta ))-\sin (\beta -\alpha ))=R(\sin (\alpha +\beta +2\theta )-sin(\beta -\alpha ))$，

和差化积，$OF=2R\cdot \sin (\beta +\theta )\cos (\alpha +\theta )$。

$D,F,G,A$ 四点共圆，则 $\angle OFP=\angle ADG$，

余角 $\angle OPF=\angle DAG=\angle BAC+\angle DAB=\alpha +\theta$，

故在 $△OPF$ 中，$OP=OF\cdot \cot (\alpha +\theta )=2R\cdot \cos (\alpha +\theta )\cos (\beta +\theta )$，

又 $OK=2R\cdot \cos \alpha \cos \beta$，

则 $PK=OK-OP=2R\cdot \cos \alpha \cos \beta -2R\cdot \cos (\alpha +\theta )\cos (\beta +\theta )$，

积化和差，$PK=R(\cos (\alpha +\beta )+\cos (\alpha -\beta )-\cos (\alpha +\beta +2\theta )-\cos (\alpha -\beta ))$，

即，$PK=R(\cos (\pi -\gamma )-\cos (\pi -(\gamma -2\theta )))=R(\cos (\gamma -2\theta )-\cos \gamma )=DF$

故可得出 $△DFL≌△KPL(\mathrm{A}\mathrm{A}\mathrm{S})$，$DL=KL$，得证。

---

证法4：中位线2

引理3

引理： 当 $CE$ 为直径时，西姆松线为 $AB$，$G$ 为垂心。此时，$AB$ 经过 $EG$ 中点。

证明：

由引理1，$GI=I{G}^{\prime }$，又由引理2，$E{G}^{\prime }//IJ$，

则 $IJ$ 为 $△G{G}^{\prime }E$ 的中位线，故 $AB$ 经过 $EG$ 中点。

定理证明

$K$ 为 $△ABC$ 的垂心，$H$ 为 $△GEC$ 的垂心。

（由于辅助线较为复杂，此处不再一一叙述）

对于 $△GEC$，$D$ 满足引理3所述的情况。

故 $EG$ 经过 $DH$ 的中点 $T$。

则可证明 $LT$ 为 $△DKH$ 的中位线，即证明 $EG//KH$，

观察可证明 $△DEG\sim △RKH$。

观察图中有大量平行，可得到大量平行四边形。

$\because DG\perp AC,EN\perp AC,QP\perp AC$

$\therefore DG//EN//QP$

$\because DE\perp EC,AU\perp EC,GO\perp EC$

$\therefore DE//AU//GO$

故有 $\angle ASG=\angle SGO=\angle Q$

所以 $△AGS\sim △BEQ$ ，$\frac{SG}{EQ}=\frac{AG}{EB}$

$D,B,C,A$ 四点共圆，有 $\angle DBE=\angle DAG$

所以 $△DBE\sim △DAG$，$\frac{AG}{EB}=\frac{DG}{DE}$

故 $\frac{DG}{DE}=\frac{SG}{EQ}$，又 $SG=RH,EG=RK$， 则 $△DEG\sim △RKH$，

故 $EG//KH$ ，$LT$ 为 $△DKH$ 的中位线，$DL=DK$，得证。

---

The End.