语音信号处理之(三)矢量量化(Vector Quantization)
语音信号处理之(三)矢量量化(Vector Quantization)zouxy09@qq.comhttp://blog.csdn.net/zouxy09 这学期有《语音信号处理》这门课,快考试了,所以也要了解了解相关的知识点。呵呵,平时没怎么听课,现在只能抱佛脚了。顺便也总结总结,好让自己的知识架构清晰点,也和大家分享下。下面总结的是第三个知识点:VQ。因为花的时间不多,所以可能会
语音信号处理之(三)矢量量化(Vector Quantization)
这学期有《语音信号处理》这门课,快考试了,所以也要了解了解相关的知识点。呵呵,平时没怎么听课,现在只能抱佛脚了。顺便也总结总结,好让自己的知识架构清晰点,也和大家分享下。下面总结的是第三个知识点:VQ。因为花的时间不多,所以可能会有不少说的不妥的地方,还望大家指正。谢谢。
矢量量化(VQ,Vector Quantization)是一种极其重要的信号压缩方法。VQ在语音信号处理中占十分重要的地位。广泛应用于语音编码、语音识别和语音合成等领域。
一、概述
VectorQuantization (VQ)是一种基于块编码规则的有损数据压缩方法。事实上,在 JPEG 和 MPEG-4 等多媒体压缩格式里都有 VQ 这一步。它的基本思想是:将若干个标量数据组构成一个矢量,然后在矢量空间给以整体量化,从而压缩了数据而不损失多少信息。
在以前,VQ运用的一个难点在于它要要解决一个多维积分(multi-dimensional integration)的问题。后来,在1980年,Linde, Buzo和Gray(LBG,这个缩写也是LBG算法的命名)提出一种基于训练序列的VQ设计算法,对训练序列的运用绕开了多维积分的求解,使得世上又诞生了一种经典的被世人称为LBG-VQ的算法!它一直延绵至今,经典永不褪色。
二、知识准备
VQ实际上就是一种逼近。它的思想和“四舍五入”有异曲同工之妙,都是用一个和一个数最接近的整数来近似表示这个数。我们先来看看一个一维VQ的例子:
这里,小于-2的数都近似为-3,在-2和0之间的数都近似为-1,在0和2之间的数都近似为1,大于2的数都近似为3。这样任意的一个数都会被近似为-3、-1、1或者3这四个数中的其中一个。而我们编码这四个数只需要两个二进制位就行了。所以这是1-dimensional,2-bit VQ,它的rate(量化速率?)为2bits/dimension。
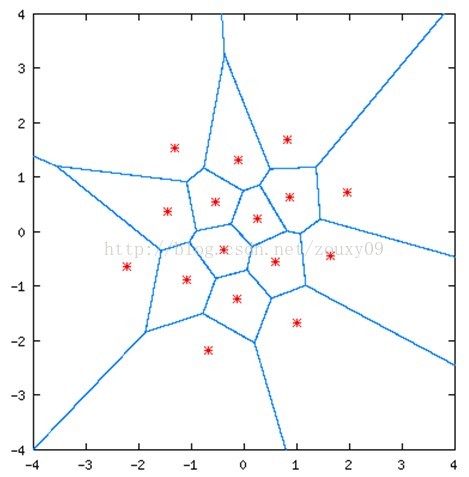
我们再看一个二维的例子:
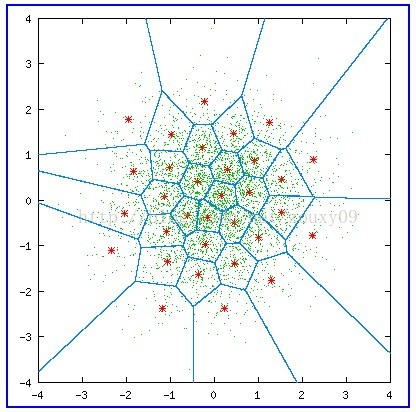
在这里,我们用蓝色实线将这张图划分为16个区域。任意的一对数(也就是横轴x和纵轴y组成的任意的一个坐标点(x, y))都会落到上面这张图中的某一特定区域。然后它就会被该区域的红星的点近似。这里有16块不同区域,就是16个红星点。然后这16个值就可以用4位的二进制码来编码表示(2^4=16)。因此,这是个2-dimensional, 4-bit VQ,它的速率同样是2bits/dimension。上面这些红星点就是量化矢量,表示图中的任意一个点都可以量化为这16个矢量中的其中一个。
对于二维,我们还可以用图像压缩来说明。类似于将图像的每个像素点当作一个数据,跑一下 K-means 聚类,假设将图像聚为k类,就会得到每类的质心centroids,共k个,然后用这些质心的像素值来代替对应的类里的所有点的像素值。这样就起到压缩的目的了,因为只需要编码k个像素值(和图像每个像素点的对这k个值得索引)就可以表示整张图像了。当然,这会存在失真了,失真的程度就是k的个数了。最偏激的就是原图像每个像素就是一个类,那就没有失真了,当然这也没有了压缩。
以上的两个例子,红星被称为码矢(codevectors)。而由蓝色边定义的区域叫做编码区域(encoding regions)。所有码矢的集合称为码书(codebook),所有编码区域的集合称为空间的划分(partition of thespace)。
三、VQ设计问题
VQ问题可以这样描述:给定一个已知统计属性的矢量源(也就是训练样本集,每一个样本是一个矢量)和一个失真测度。还给定了码矢的数量(也就是我们要把这个矢量空间划分为多少部分,或者说量化为多少种值),然后寻找一个具有最小平均失真度(数据压缩,肯定是失真越小越好)的码书(所有码矢的集合,也就是上面的那些所有红色星星点)和空间的划分(图中所有蓝色线的集合)。
假定我们有一个有M个矢量源(训练样本)的训练序列(训练集):T={x1, x2,…, xM};
这个训练序列可以通过一些大数据库得到。例如如果这个矢量源是语音的话,那么我们就可以对一些电话录音裁剪得到。我们假设M足够大(训练样本足够多),这样才可以保证这个训练序列包含了源的所有统计特性。我们假设源矢量是k维的:
xm=(xm,1,xm,2, …, xm,k), m=1,2,…,M
假设码矢的数目是N(也就是我们要把这个矢量空间划分为N个部分,或者说量化为N种值),码书(所有码矢的集合)表示为:C={c1, c2,…, cN};
每一个码矢是个k维向量:cn=(cn,1, cn,2, …, cn,k),n=1,2,…,N;
与码矢cn对应的编码区域表示为Sn,然后将空间的划分表示为:P={S1, S2,…,SN};
如果源矢量xm在Sn内,那么它的近似(用Q(xm)表示)就是cn,
Q(xm)=cn, 如果xm 属于Sn
假设我们采用均分误差失真度量,那么平均失真度表示如下:
这里||e||2为欧式距离。
那么设计问题就可以简单的描述为:给定T(训练集)和N(码矢数目),找到能使Dave(平均失真度)最小的C(码书)和P(空间划分)。
四、优化准则
如果C和P是上面这个最小化问题的一个解,那么这个解需要满足以下两个条件:
1)Nearest NeighborCondition 最近邻条件:
这个条件的意思是编码区域Sn应该包含所有与cn最接近的矢量(相比于与其他码矢的距离)。对于在边界(蓝色线)上面的矢量,需要采用一些决策方法(any tie-breaking procedure)。
2)Centroid Condition质心条件:
这个条件要求码矢cn是编码区域Sn内所有的训练样本向量的平均向量。在实现中,需要保证每个编码区域至少要有一个训练样本向量,这样上面这条式的分母才不为0。
五、LBG算法
LBG-VQ算法是一个迭代算法,它交替地调整P和C(解上面这两个优化准则),使失真度不断地趋向于它的局部最小值(有点EM的思想哦)。这个算法需要一个初始的码书C(0)。这个初始码书可以通过分裂(splitting)方法得到。这个方法主要是把一个初始码矢设置为所有训练样本的平均值。然后把这个码矢分裂成两个(分裂的方式见下面的LBG算法的第3步的公式,只要是乘以一个扰乱系数)。把这两个码矢作为初始的码书,然后迭代算法就在这个初始的码书上面跑。它每一次都将每个码矢分裂为2个,重复这个过程,直到获得要求的码矢个数。1个分裂为2个,2个分裂为4个,4个分裂为8个……
LBG算法:
1、给定训练集T。固定ɛ(失真阈值)为一个很小的正数。
2、让N=1(码矢数量),将这一个码矢设置为所有训练样本的平均值:
计算总失真度(这时候的总失真很明显是最大的):
3、分裂:对i=1,2,…,N,他们的码矢分别为:
让N=2N,就是每个码矢分裂(乘以扰乱系数1+ɛ和1-ɛ)为两个,这种每一次分裂后的码矢数量就是前一次的两倍。
4、迭代:让初始失真度为: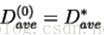
1)对于训练集T中的每一个训练样本m=1,2,…,M。在所有码矢中寻找的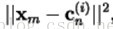
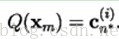
2)对于n=1,2,…,N,通过以下方式更新所有码矢:
也就是将所有属于cn所在的编码区域Sn的训练样本取平均作为这个编码区域的新的码矢。
3)迭代计数器加1:i=i+1.
4)计算在现阶段的C和P基础上的总失真度:
5)如果失真度相比上一次的失真度(相对失真改进量)还大于可以接受的失真阈值ɛ(如果是小于就表明再进行迭代运算失真得减小是有限的以停止迭代运算了),那么继续迭代,返回步骤1)。
6)否则最终失真度为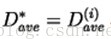
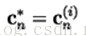
5、重复步骤3和4至到码矢的数目达到要求的个数。
六、二维模拟
二维模拟动画点击这里http://www.data-compression.com/vqanim.shtml(这里吐槽一下,为什么CSDN不支持gif动画的插入呢?)
1)训练样本集是由零均值和单位方差的高斯分布产生。
2)小的绿色的点就是这些训练样本。有4096个。
3)我们把阈值设置为ɛ=0.001。
4)这个算法会保证得到一个局部最小解。
5)训练序列需要足够的大,建议M>=1000N。
七、参考资料:
[1]http://www.data-compression.com/vq.html
[2]漫谈Clustering (番外篇): Vector Quantization: http://blog.pluskid.org/?p=57
[3] lbgvq.c --- C program forLBG VQ design

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献13条内容
已为社区贡献13条内容

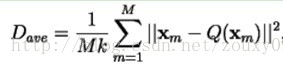
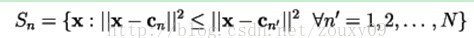

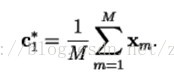
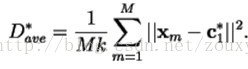
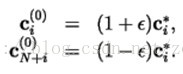
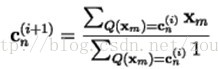
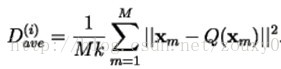
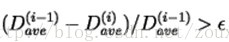





所有评论(0)