二维正态分布的表达式：
f ( x , y ) = 1 2 π σ 1 σ 2 1 − ρ 2 exp ⁡ { − 1 2 ( 1 − ρ 2 ) [ ( x − μ 1 ) 2 σ 1 2 − 2 ρ ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 + ( y − μ 2 ) 2 σ 2 2 ] } f(x,y)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\{-\frac{1}{2(1-\rho^2)}[\frac{(x-\mu_1)^2}{\sigma_1^2}-\frac{2\rho(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2}]\} f(x,y)=2πσ1​σ2​1−ρ2 ​1​exp{−2(1−ρ2)1​[σ12​(x−μ1​)2​−σ1​σ2​2ρ(x−μ1​)(y−μ2​)​+σ22​(y−μ2​)2​]}
其中${\mu }_1,{\mu }_2$ 为均值，${\sigma }_1^2,{\sigma }_2^2$为方差，$\rho$为相关系数，且$-1<\rho <1$。

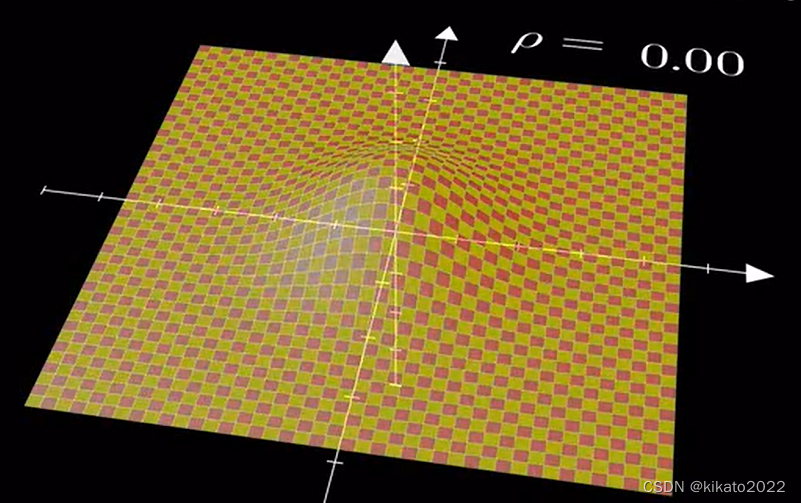
先用一些大致的图像来感受相关系数对二维正态分布的影响

三维立体图

散点图

从图象上我们大致可以看出，当 $\rho$ 从 $0$ 向无限接近于 $1$ 变化的过程中，图像越来越向 直线$y=x$集中；当 $\rho$ 从 $0$ 向无限接近于 $-1$ 变化的过程中，图像越来越向 直线 $y=-x$ 集中。这与我们对相关系数的认识是一致的。那么，现在我们从表达式的角度来分析，相关系数为什么会对图像带来这样的影响。

对表达式进行分析

为了分析简单，我采用控制变量法，令${\mu }_1={\mu }_2=0，{\sigma }_1={\sigma }_2=1$.
此时有
f ( x , y ) = 1 2 π 1 − ρ 2 exp ⁡ { − 1 2 ( 1 − ρ 2 ) [ x 2 − 2 ρ x y + y 2 } f(x,y)= \frac{1}{2\pi\sqrt{1-\rho^2}}\exp\{-\frac{1}{2(1-\rho^2)}[x^2-2\rho xy+y^2\} f(x,y)=2π1−ρ2 ​1​exp{−2(1−ρ2)1​[x2−2ρxy+y2}
我们把式子改写为：
f ( x , y ) = 1 2 π 1 − ρ 2 exp ⁡ { − 1 2 ( 1 − ρ 2 ) [ ( x − ρ y ) 2 + ( 1 − ρ 2 ) y 2 } = e − y 2 2 2 π 1 − ρ 2 exp ⁡ { − 1 2 ( 1 − ρ 2 ) [ ( x − ρ y ) 2 } \begin{align*} f(x,y) &= \frac{1}{2\pi\sqrt{1-\rho^2}}\exp\{-\frac{1}{2(1-\rho^2)}[(x-\rho y)^2+(1-\rho^2) y^2\}\\ &= \frac{e^{-\frac{y^2}{2}}}{2\pi\sqrt{1-\rho^2}} \exp\{-\frac{1}{2(1-\rho^2)}[(x-\rho y)^2\} \end{align*} f(x,y)​=2π1−ρ2 ​1​exp{−2(1−ρ2)1​[(x−ρy)2+(1−ρ2)y2}=2π1−ρ2 ​e−2y2​​exp{−2(1−ρ2)1​[(x−ρy)2}​
$\rho$ 对图像对称中心的影响
从上式我们可以看出，当 $y$ 取一定的值的时候，$f(x,y)$是关于$x=\rho y$对称的，也就是关于$x$ 的类正态分布（叫类正态分布是因为它的形状和正态分布基本一样，但是前面系数多了个 $e^{-\frac{y^2}{2}}$，所以概率密度的积分不唯一）。

若 $\rho =0,y=0$ 图像就退化成 $x$ 的一维正态分布，若 $\rho =0,y=a\ne 0$, 图像就退化成 $x$ 的类正态分布，但只要 $\rho =0$， 关于 $x$ 的类正态分布的中心点是不受 $y$ 影响的。

用一句更直接的话说，当固定 $y$ 的值，关于 $x$ 的类正态分布的中心点一定在 $x=\rho y$ 这条直线上，也就是说，点(X,Y)出现概率最高的点一定在 $x=\rho y$ 这条直线附近。

$\rho$ 对图像集中程度的影响
我们可以看到，上式中$\rho$出现的地方除了在分子$(x-\rho y{)}^2$中，还出现在了指数的分母和左边系数的分母中,这其实是一维正态分布方差出现的位置，甚至我们可以这样说：

f ( x ) = 1 2 π 1 − ρ 2 exp ⁡ { − 1 2 ( 1 − ρ 2 ) [ ( x − ρ y ) 2 } f(x) = \frac{1}{2\pi\sqrt{1-\rho^2}} \exp\{-\frac{1}{2(1-\rho^2)}[(x-\rho y)^2\} f(x)=2π1−ρ2 ​1​exp{−2(1−ρ2)1​[(x−ρy)2}

在上面我们抽离出来分析的表达式中，$1-{\rho }^2$ 起到的是方差的作用，而 $\rho y$ 起到的是均值的作用，所以当 $\rho$ 越接近于0，该表达式的方差越大，关于$x$的正态分布的图像越平，当$rho$越接近于1，该表达式的方差越接近于0，关于$x$的正态分布的图像越尖。

这基本从表达式的角度说明了，为什么当 $\rho$ 从 0 向 $1(-1)$ 变化的过程中，图像从环状的散点图，变成了集中于$y=x(y=-x)$的线状的散点图。

另外由于系数 $\frac{e^{-\frac{y^2}{2}}}{2\pi \sqrt{1-{\rho }^2}}$ 的中 $e^{-\frac{y^2}{2}}$ 项的存在，位于图像的绝对中心点 $x=0,y=0$ 附近出现的概率密度总是最大的。举例来说，固定 $y=0$ 和固定 $y=1$，关于 $x$的类正态分布形状几乎一模一样，但是$y=1$的图像比$y=0$的图像矮。这也解释了为什么散点图总是一个椭圆状，而不是长方形状。

总结

如果把${\mu }_1,{\mu }_2$ 和 ${\sigma }_1^2,{\sigma }_2^2$对图像的影响加入进来，讨论要复杂一些，但是 $\rho$ 对图像的影响的基本方向不会变，有集中程度和对称中心两方面的影响。其实${\mu }_1，{\mu }_2$也不过是把图像的对称中心从 $(0,0)$ 转移到了 $({\mu }_1,{\mu }_2)$，而 ${\sigma }_1,{\sigma }_2$若是不相等，就是$\rho =0$ 时的圆环状散点图会变成椭圆环状散点图，之后将$\rho$ 从 $0$ 到 $1(-1)$ 进行变化，变化趋势是一样的。至于这个二维正态分布的表达式是怎么推出来的，请看我另外一篇文章。