【数据库】— 无损连接、Chase算法、保持函数依赖
无损连接和保持函数依赖是关系数据库设计中的两个重要概念。无损连接指的是在关系模式分解过程中,如果原始关系模式中存在某些函数依赖关系,那么这些函数依赖关系应该在分解后的新关系模式中仍然能够被保持。也就是说,无论是在原始的关系模式中还是在分解后的新关系模式中,都应该能够通过关联操作(join)来获取与原始关系模式相同的信息。保持函数依赖指的是在关系模式分解过程中,如果原始关系模式中存在某些函数依赖关系
【数据库】— 无损连接、Chase算法
Chase算法
形式化定义:
- 构造一个 k k k行 n n n列的表格,每行对应一个模式 R i ( 1 ≤ i ≤ k ) Ri (1≤i ≤ k) Ri(1≤i≤k),每列对应一个属性 A j ( 1 ≤ j ≤ n ) Aj( 1≤j≤ n) Aj(1≤j≤n),若 A j Aj Aj在 R i Ri Ri中,则在表格的第 i i i行第 j j j列处填上 a j aj aj,否则填上符号 b i j bij bij
- 检查
F
F
F的每个
F
D
FD
FD,并修改表格中的元素,方法如下:
- 对于F中的函数依赖
X
→
Y
X→Y
X→Y,若表格中有两行在
X
X
X分量上相等,在
Y
Y
Y分量
上不相等,则修改 Y Y Y:- 若 Y Y Y的分量中有一个 a j aj aj,则另一个也修改为 a j aj aj;
- 如果没有 a j aj aj,则用其中一个 b i j bij bij替换另一个符号( i i i是所有 b b b中最小的行数) ,一直到表格不能修改为止
- 对于F中的函数依赖
X
→
Y
X→Y
X→Y,若表格中有两行在
X
X
X分量上相等,在
Y
Y
Y分量
- 若修改后,表格中有一行是全
a
a
a,即
a
1
a
2
…
a
n
a1a2…an
a1a2…an,则
p
p
p相对于
F
F
F是无损连接的分解,否则不是
举例:
关系模式: R ( A , B , C , D , E ) 分解: R 1 ( A , D ) , R 2 ( A , B ) , R 3 ( B , E ) , R 4 ( C , D , E ) , R 5 ( A , E ) 函数依赖: F = { A → C , B → C , C → D , D E → C , C E → A } 判断 R 分解为 p = R 1 , R 2 , R 3 , R 4 , R 5 是否是无损连接的分解 关系模式:R(A,B,C,D,E)\\ {}\\ 分解:R1(A,D), R2(A,B), R3(B,E), R4(C,D,E), R5(A,E)\\ {}\\ 函数依赖:F=\{A→C, B→C, C→D, DE→C, CE→A\}\\ {}\\ 判断R分解为p={R1,R2,R3,R4,R5}是否是无损连接的分解 关系模式:R(A,B,C,D,E)分解:R1(A,D),R2(A,B),R3(B,E),R4(C,D,E),R5(A,E)函数依赖:F={A→C,B→C,C→D,DE→C,CE→A}判断R分解为p=R1,R2,R3,R4,R5是否是无损连接的分解
Chase算法举例
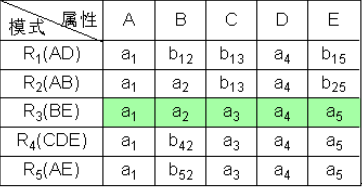
① 构造一个初始的二维表若“属性”属于“模式”中的属性,则填aj,否则填bij

② 根据A→C,对上表进行处理,由于属性列A上第1、2、5行相同均为a1,所以将属性列C上的b13、b23、b53改为同一个符号b13(取行号最小值)。

③ 根据B→C,对上表进行处理,由于属性列B上第2、3行相同均为a2,所以将属性列C上的b13、b33改为同一个符号b13(取行号最小值)。

④ 根据C→D,对上表进行处理,由于属性列C上第1、2、3、5行相同均为b13,所以将属性列D上的值均改为同一个符号a4。

⑤ 根据DE→C,对上表进行处理,由于属性列DE上第3、4、5行相同均为a4a5,所以将属性列C上的值均改为同一个符号a3。

⑥ 根据CE→A,对上表进行处理,由于属性列CE上第3、4、5行相同均为a3a5,所以将属性列A上的值均改为同一个符号a1。

⑦ 通过上述的修改,使第三行成为 a 1 a 2 a 3 a 4 a 5 a1a2a3a4a5 a1a2a3a4a5,则算法终止。且分解具有无损连接性。
一种简便方法:分解为两个模式时

无损连接和函数依赖的一个简单例子


开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献22条内容
已为社区贡献22条内容





所有评论(0)