本篇文章是博主在通信等领域学习时，用于个人学习、研究或者欣赏使用，并基于博主对通信等领域的一些理解而记录的学习摘录和笔记，若有不当和侵权之处，指出后将会立即改正，还望谅解。文章分类在通信领域笔记：

          通信领域笔记（6）---《现代谱估计分析信号的功率谱（2）---Pisarenko 谐波分解法》

现代谱估计分析信号的功率谱（2）---Pisarenko 谐波分解法

目录

2.3 谐波模型谱估计

2.4 Pisarenko 谐波分解法

3.2 Pisarenko 谐波分解法功率谱估计

4 总结分析

---

本文接上文《现代谱估计分析信号的功率谱（1）---AR 模型谱估计》

AR 模型谱估计分析方法见通信领域笔记专栏：

        《现代谱估计分析信号的功率谱（1）---AR 模型谱估计》

2.3 谐波模型谱估计

        上一节讨论了信号建模谱估计方法，信号模型是被白噪声激励的线性时不变系统。在许多实际应用中，感兴趣的信号是包含在白噪声中的正弦信号，在这种情况下正弦函数或者谐波模型更加适用。

        对在噪声中发现的复指数信号，感兴趣的参数是信号的频率。考虑一个噪声中的复指数信号模型，设信号由 p 个复指数信号组成

        谐波模型谱估计的关键任务是谐波个数及频率的估计，采用主要特征分解法，即通过分解输入信号𝑦(𝑛)的自相关矩阵的特征值和特征向量得到两个子空间，其中最大的若干特征值对应的特征向量构成信号子空间，最小的若干特征值对应的特征向量构成噪声子空间，同时两个子空间正交。

        谐波模型谱估计的主要方法包括 Pisarenko 谐波分解法、多重信号分类 (MUSIC)方法和旋转不变参数估计计(ESPRIT)方法。这里主要介绍 Pisarenko 谐波分解法，同时利用 MATLAB 实现Pisarenko 对信号的谱估计。

2.4 Pisarenko 谐波分解法

---

3.2 Pisarenko 谐波分解法功率谱估计

根据 2.4 节所介绍的方法，可将 Pisarenko 谐波分解法归纳为以下几个步骤：

        (1) 根据观测信号求解自相关矩阵 Ry；

        (2) 根据自相关矩阵 Ry 求特征值和特征向量，其中特征值最小的为噪声对应的特征值；

        (3) 选取最小特征值对应的特征向量计算特征多项式的根；

        (4) 特征根对应的频率即为分解得到的谐波频率，一般取正值；

        (5) 根据得到的频点计算对应频点的功率值。

         按照上述步骤利用 MATLAB 进行谐波分解仿真。首先计算自相关矩阵 Ry；

clc,clear all,close all
w=2*pi*[0.05 0.40 0.42];
varia=0.32;
i=1;
k=1;
for varia=0.32:0.01:6
    i=1;
    f_estmt=zeros(20,3);
    for i=1:20
        Rline=zeros(1,255);
        R=zeros(7,7);
        smp=fix(100*rand);
        Z=randn(1,128)*sqrt(varia);
        a=zeros(1,4);
        n=smp:smp+127;
        X=2*cos(w(1)*n)+3*cos(w(2)*n)+1.2*cos(w(3)*n);
        Y=(X+Z)';
        Rline=xcorr(Y');
        for ii=1:7
            R(ii,:)=Rline(129-ii:135-ii);
        end
        [eigvct,eigval]=eig(R);
        [C,Ind]=min(diag(eigval));
        z=roots(eigvct(:,Ind));
        longz=length(unique(abs(angle(z))/2/pi));
        a(1:longz)=sort(unique(abs(angle(z))/2/pi))';
        maxtop3=sort(a);
        %gettop3maxvalue
        f_estmt(i,1:3)=maxtop3(2:4);
    end
    meanS(k,1:3)=mean(f_estmt);
    VarS(k,1:3)=var(f_estmt);
    k=k+1;
end

figure;
subplot(2,1,1)
h=gca;
set(h,'FontSize',16);
x=linspace(0.32,6,569);
plot(x,meanS(:,1),'-.r',x,meanS(:,2),'b',x,meanS(:,3),'k+');
ylabel('Mean Estimated Frequency');
xlabel('Noise VAR');
title('Mean Frequency trends');
legend('0.05','0.40','0.42');

subplot(2,1,2)
h=gca;%
set(h,'FontSize',16);%
x=linspace(0.32,6,569);
plot(x,VarS(:,1),'-.r',x,VarS(:,2),'b',x,VarS(:,3),'k+');
ylabel('Variance of Estimated Frequency');
xlabel('NoiseVAR');
title('Frequency Variance trends');
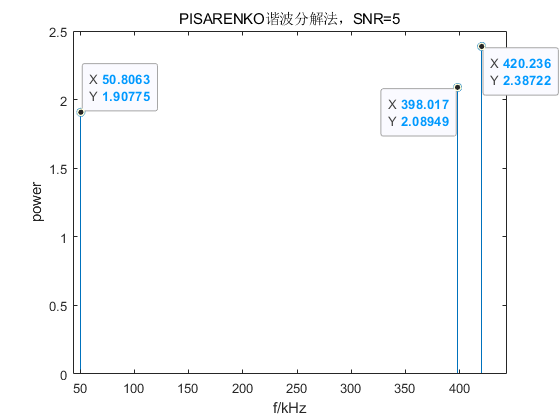
legend('0.05','0.40','0.42');

        我们测试了在不同信噪比情况下 Pisarenko 谐波分解法的性能（默认阶数 P为 3），并进行了对比，结果如下：

        从以上结果可以看出，Pisarenko 谐波分解法对噪声较为敏感，在低信噪比情况下效果较差，频点估计不准确，并且功率与原信号相比也有较大差距。随着信噪比的提升，频点估计的准确程度上升的同时，信号功率也更加稳定，偏差变小。

        为了进一步验证试验结果，我们在更高信噪比下进行的试验，结果如下：

        可以看出，在高信噪比下，Pisarenko 谐波分解法的分解效果较好。

---

     文章若有不当和不正确之处，还望理解与指出。由于部分文字、图片等来源于互联网，无法核实真实出处，如涉及相关争议，请联系博主删除。如有错误、疑问和侵权，欢迎评论留言联系作者，或者关注VX公众号：Rain21321，联系作者。