参考书目：《神经计算建模实战——基于brainpy》 吴思

0 引言

        之前的章节介绍了单个神经元的建模，而神经元与神经元之间通过突触相连接，从而形成了一个网络。因此，要形成整个网络还需要对突触进行建模。

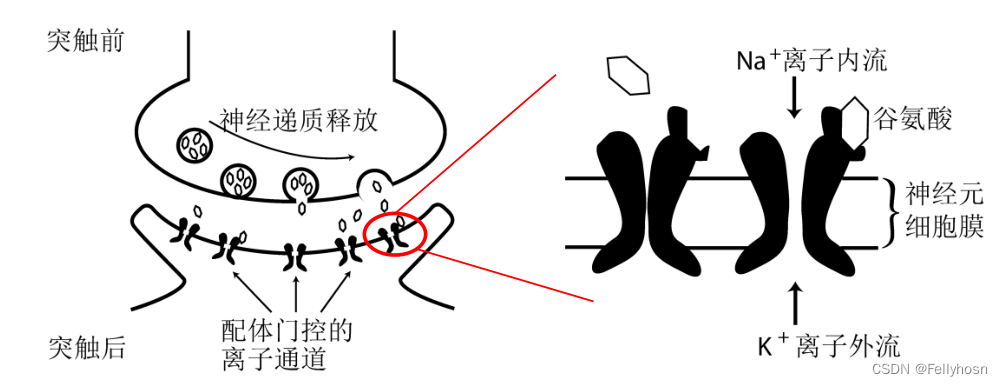
        突触可分为化学突触和电突触，前者一般情况下由突触前膜、突触间隙和突触后膜组成；电突触中，两个神经元之间的连接结构被称为间隙连接，两个神经元的细胞膜靠的非常近。

1 化学突触概述

        化学突触的组成属于高中生物知识，这里主要补充几个概念：

  1. 突触后电位（PSP）：突触后膜离子通道开放引起的膜电位变化 ，分为兴奋性（EPSP）和抑制性（IPSP）
  2. 离子型受体：与神经递质结合后，离子通道状态发生改变的受体。反应较为迅速
  3. 代谢型受体：与神经递质结合后，化学反应过程发生改变的受体。反应较慢
  4. 现象学模型：完全根据突触前的神经递质到达突触后神经元产生的电流形状建模
  5. 生理学模型：根据突触后膜各个离子通道的动力学性质进行建模

本章节介绍了一些常见的突触模型。

2 化学突触的现象学模型

2.1 化学突触的现象学模型概述

        化学突触将电信号从突触前神经元传递到突触后神经元，输入为突触前神经元的脉冲信号，输出是突触后电流（PSC）。

        一般而言，突触后电流可根据欧姆定律求出：I_{syn}=g(V_{post}-E_{syn})，其中g为突触上受体的电导，V_{post}和E_{syn}分别表示突触后电位和突触的反转膜电位（控制膜电位的正负）。此时，突触的建模转化为了对电导g的建模（称为电导模型） 在现象学模型中，我们将g看作一个随时间变化的函数g(t)。

        实际情况中，还可以将上述方程进一步简化，将V_{post}设为定值，例如细胞的静息膜电位。这么做的原因是动作电位持续时间非常短，相较于阈下波动的时长可以忽略不计。此时的模型表达式为：I_{syn}=g(t)(V_{post_rest}-E_{syn})。通过这种方式，我们将神经元的建模转化为了对突触后膜电流I_{syn}的计算，这种模型称为电流模型。之后的几种模型都会分电导模型和电流模型来实现。

        对于突触后膜的反转电位E_{syn}，其往往决定突触的电流特性。当反转电位明显高于细胞静息膜电位时，突触在突触后神经元传递突触后兴奋电流，反之则为抑制性突触后电流。

        对于g(t)，在静息状态下离子通道关闭，电导为0；在动作电位传到突触前膜时，离子通道开放，g(t)增大；神经递质与受体结合一段时间后离子通道关闭，电导又变为0。因此，g(t)的变化完全是由突触前神经元的脉冲引起的，因此可写作：g(t)=\overline{g}\displaystyle\sum_{t^{(f)}}s(t-t^{(f)})，其中t^{(f)}代表脉冲到达突触的时刻。

2.2 电压跳变模型

        电压跳变模型是现象学模型的基础，也被称为δ模型。跳变，顾名思义，指的是突触脉冲到来时膜电位快速上升和下降，产生突变的效果。电压跳变模型将突触效应建模为瞬间的突触后膜电位变化：V_{post}=V_{post}+wH(t)。w为突触权重，其值的正负代表了突触是兴奋性/抑制性突触；H(t)为Heaviside函数，t≥0时取1否则取0。

        电压跳变模型假设突触前神经元传来脉冲后，突触后膜的离子通道瞬间打开，又瞬间关闭。因此该模型只适用于具有快速动力学的突触。实现代码如下：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class VoltageJump(bp.dyn.TwoEndConn):
    def __init__(self,pre,post,conn,g_max=1.,delay_step=2,E=0.,**kwargs):
        super().__init__(pre=pre,post=post,conn=conn,**kwargs)

        self.g_max = g_max
        self.delay_step = delay_step
        self.E = E
        self.pre2post = self.conn.require('pre2post') #获取从pre到post的连接信息

        self.g = bm.Variable(bm.zeros(self.post.num))
        self.delay = bm.LengthDelay(self.pre.spike,delay_step) #定义延迟处理器

    def update(self,tdi):
        delayed_pre_spike = self.delay(self.delay_step)
        #取出delay_step时间步长的突触前脉冲信号
        self.delay.update(self.pre.spike)
        #根据最近的突触前脉冲信号 更新延迟变量

        #根据连接模式，计算各个突触后神经元收到的信号强度
        post_sp = bm.pre2post_event_sum(delayed_pre_spike,self.pre2post,self.post.num,self.g_max)
        #pre2post_event_sum函数：整合突触前神经元传给突触后神经元的信号
        self.g.value = post_sp
        #计算突触后效应
        self.post.V += self.g

        代码采用conn.require函数得到从突触前神经元到突触后神经元的连接信息；在update函数中使用pre2post_event_sum来整合突触前神经元传给突触后神经元的脉冲信号。

        进行模拟，让突触前神经元在20\60\100\140\180ms产生动作电位，观察突触后神经元膜电位变化情况：

#定义突触前后神经元和突触，并构建神经网络
neu1 = bp.neurons.SpikeTimeGroup(1,times=(20,60,100,140,180),indices=[0,0,0,0,0])
neu2 = bp.neurons.HH(1,V_initializer=bp.init.Constant(-70.68))
syn1 = VoltageJump(neu1,neu2,conn=bp.connect.All2All(),g_max=2.)
net = bp.dyn.Network(pre=neu1,syn=syn1,post=neu2)

#构建模拟器
runner = bp.dyn.DSRunner(net,monitors=['pre.spike','post.V','syn.g'])
runner.run(500)

#可视化
fig,gs = bp.visualize.get_figure(3,1,1.5,6.)
ax = fig.add_subplot(gs[0,0])
plt.plot(runner.mon.ts,runner.mon['pre.spike'],label='pre.spike')
plt.legend(loc='upper right')
plt.title('Delta Synapse Model')
plt.xticks([])
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax = fig.add_subplot(gs[1,0])
plt.plot(runner.mon.ts,runner.mon['syn.g'], label='g', color=u'#d62728')
plt.legend(loc='upper right')
plt.xticks([])
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax = fig.add_subplot(gs[2,0])
plt.plot(runner.mon.ts, runner.mon['post.V'], label='post.V')
plt.legend(loc='upper right')
plt.xlabel('Time [ms]')
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.show()

        post.V（即突触后神经元的膜电位） 在spike时产生了突变。

2.3 指数衰减模型

         在电压跳变模型的基础上，指数衰减模型描述了神经递质和受体结合数量随时间指数下降的过程，公式如下：s(t)=\left\{\begin{matrix} e^{-t/\tau}\quad t\geq 0 \\ 0 \quad t<0 \end{matrix}\right. =e^{-t/\tau}H(t)，写为微分形式：\frac{ds}{dt}=-\frac{s}{\tau}+\delta(t)。g(t)为s(t)的线性求和，求得：\frac{dg}{dt}=-\frac{g}{\tau}+\overline{g}\displaystyle\sum_{t^{(f)}}\delta(t-t^{(f)})

        其代码实现如下：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class Exponential(bp.dyn.TwoEndConn):
    def __init__(self,pre,post,conn,g_max=5.,tau=12.,delay_step=2,E=0.,V_rest=-65.,
                 syn_type='CUBA',method='exp_auto',**kwargs):
        super(Exponential,self).__init__(pre=pre,post=post,conn=conn,**kwargs)
        self.tau = tau
        self.g_max = g_max
        self.E = E
        self.V_rest = V_rest
        self.delay_step = delay_step
        assert syn_type in ['CUBA','COBA']
        self.type = syn_type
        self.pre2post = self.conn.require('pre2post')

        self.g = bm.Variable(bm.zeros(self.post.num))
        self.delay = bm.LengthDelay(self.pre.spike,delay_step)

        self.integral = bp.odeint(self.derivative,method=method)

    def derivative(self,g,t):
        dgdt = -g/self.tau
        return dgdt
    def update(self,tdi):
        delayed_pre_spike = self.delay(self.delay_step)
        self.delay.update(self.pre.spike)

        post_sp = bm.pre2post_event_sum(delayed_pre_spike,self.pre2post,self.post.num,self.g_max)
        self.g.value = self.integral(self.g,tdi.t,tdi.dt)+post_sp

        if self.type == 'CUBA':
            self.post.input += self.g * (self.E - self.V_rest)
        else:
            self.post.input += self.g * (self.E - self.post.V)

        分别采用电流模型和电导模型计算突触后电流，模拟突触前神经元在25/50/75/100/160时刻发放脉冲：

def run_syn(syn_model,title,run_duration=200.,sp_times=(10,20,30),**kwargs):
    neu1 = bp.neurons.SpikeTimeGroup(1,times=sp_times,indices=[0]*len(sp_times))
    neu2 = bp.neurons.HH(1, V_initializer=bp.init.Constant(-50.68))
    syn1 = syn_model(neu1,neu2,conn=bp.connect.All2All(),**kwargs)
    net = bp.dyn.Network(pre=neu1,syn=syn1,post=neu2)

    #进行模拟
    runner = bp.dyn.DSRunner(net,monitors=['pre.spike', 'post.V', 'syn.g', 'post.input'])
    runner.run(run_duration)

    #可视化
    fig,gs = bp.visualize.get_figure(7,1,0.5,6.)
    ax = fig.add_subplot(gs[0,0])
    plt.plot(runner.mon.ts, runner.mon['pre.spike'], label='pre.spike')
    plt.legend(loc='upper right')
    plt.title(title)
    plt.xticks([])
    ax.spines['top'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['right'].set_visible(False)

    ax = fig.add_subplot(gs[1:3,0])
    plt.plot(runner.mon.ts,runner.mon['syn.g'],label = 'g', color=u'#d62728')
    plt.legend(loc='upper right')
    plt.xticks([])
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax = fig.add_subplot(gs[3:5,0])
    plt.plot(runner.mon.ts,runner.mon['post.input'], label='PSC', color=u'#d62728')
    plt.legend(loc='upper right')
    plt.xticks([])
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax = fig.add_subplot(gs[5:7,0])
    plt.plot(runner.mon.ts,runner.mon['post.V'],label='post.V')
    plt.legend(loc='upper right')
    plt.xlabel('Time [ms]')
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    plt.show()
run_syn(Exponential,sp_times=[25,50, 75, 100, 160],title='Exponential Synapse Model(Current-Based)',syn_type='CUBA',)
run_syn(Exponential,sp_times=[25, 50, 75, 100, 160],title='Exponential Synapse Model (Conductance-Based)',syn_type='COBA',)

         电流模型和电导模型在突触后神经元产生动作电位时有比较大的差异，是因为突触后神经元脉冲发放较多，突触后膜电位变化剧烈。可以调整gmax等一系列参数的值来调整该模型。

2.4 Alpha函数模型

        指数衰减模型虽然建模出了电导的缓慢下降，但没有建模出电导的缓慢上升过程。Alpha函数模型采用双指数形式模拟g的变化过程，并用参数\tau对电导上升/下降的速率进行控制，其表达式如下：s(t)=te^{-t/\tau}H(t)\Rightarrow \frac{ds}{dt}=(1-\frac{t}{\tau})e^{-t/\tau}H(t)。令r(t)=e^{-t/\tau}H(t)，得到g(t)的微分表达式：\frac{dg}{dt}=-\frac{g}{\tau}+\overline{g}\displaystyle\sum_{t^{(f)}}\delta(t-t^{(f)})\frac{dg}{dt}=-\frac{g}{\tau}+h, \frac{dh}{dt}=-\frac{h}{\tau}+\overline{g}\displaystyle\sum_{t^{(f)}}\delta(t-t^{(f)})。

        取\tau=5，模拟代码如下：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class Alpha(bp.dyn.TwoEndConn):
    def __init__(self, pre, post, conn, g_max=5, tau=5., delay_step=2,
                 E=0., V_rest=-65., syn_type='CUBA',method='exp_auto', **kwargs):
        super(Alpha, self).__init__(pre=pre, post=post, conn=conn, **kwargs)
        self.tau = tau
        self.g_max = g_max
        self.E = E
        self.V_rest = V_rest
        self.delay_step = delay_step
        assert syn_type in ['CUBA', 'COBA']
        self.type = syn_type
        self.pre2post = self.conn.require('pre2post')

        self.g = bm.Variable(bm.zeros(self.post.num))
        self.h = bm.Variable(bm.zeros(self.post.num))
        self.delay = bm.LengthDelay(self.pre.spike, delay_step)

        self.ini_h = bp.odeint(method=method,f=lambda h,t: -h/self.tau)
        self.int_g = bp.odeint(method=method,f=lambda g,t,h: -g/self.tau+h)

    def update(self, tdi):
        delayed_pre_spike = self.delay(self.delay_step)
        self.delay.update(self.pre.spike)

        post_sp = bm.pre2post_event_sum(delayed_pre_spike, self.pre2post, self.post.num, self.g_max)
        self.h.value = self.ini_h(self.h,tdi.t,tdi.dt)+post_sp
        self.g.value = self.int_g(self.g, tdi.t, self.h,tdi.dt)

        if self.type == 'CUBA':
            self.post.input += self.g * (self.E - self.V_rest)
        else:
            self.post.input += self.g * (self.E - self.post.V)


def run_syn(syn_model, title, run_duration=200., sp_times=(10, 20, 30), **kwargs):
    neu1 = bp.neurons.SpikeTimeGroup(1, times=sp_times, indices=[0] * len(sp_times))
    neu2 = bp.neurons.HH(1, V_initializer=bp.init.Constant(-50.68))
    syn1 = syn_model(neu1, neu2, conn=bp.connect.All2All(), **kwargs)
    net = bp.dyn.Network(pre=neu1, syn=syn1, post=neu2)

    # 进行模拟
    runner = bp.dyn.DSRunner(net, monitors=['pre.spike', 'post.V', 'syn.g', 'post.input'])
    runner.run(run_duration)

    # 可视化
    fig, gs = bp.visualize.get_figure(7, 1, 0.5, 6.)
    ax = fig.add_subplot(gs[0, 0])
    plt.plot(runner.mon.ts, runner.mon['pre.spike'], label='pre.spike')
    plt.legend(loc='upper right')
    plt.title(title)
    plt.xticks([])
    ax.spines['top'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['right'].set_visible(False)

    ax = fig.add_subplot(gs[1:3, 0])
    plt.plot(runner.mon.ts, runner.mon['syn.g'], label='g', color=u'#d62728')
    plt.legend(loc='upper right')
    plt.xticks([])
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax = fig.add_subplot(gs[3:5, 0])
    plt.plot(runner.mon.ts, runner.mon['post.input'], label='PSC', color=u'#d62728')
    plt.legend(loc='upper right')
    plt.xticks([])
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax = fig.add_subplot(gs[5:7, 0])
    plt.plot(runner.mon.ts, runner.mon['post.V'], label='post.V')
    plt.legend(loc='upper right')
    plt.xlabel('Time [ms]')
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    plt.show()
run_syn(Alpha, sp_times=[25, 50, 75, 100, 160], title='Alpha Synapse Model (Current-Based)', syn_type='CUBA',)
run_syn(Alpha, sp_times=[25,50, 75, 100, 160], title='Alpha Synapse Model (Conductance-Based)', syn_type='COBA',)

         相比指数衰减模型，Alpha模型实现了电导的缓慢上升和下降，但是其速度都是由同一个参数\tau控制的，这也导致Alpha函数模型有一定的限制。而双指数衰减模型则解决了这个问题。

2.5 双指数衰减模型

        在Alpha模型的基础上，双指数衰减模型采用两个参数分别控制电导的上升和下降过程。其表达式为：

         其中k=a(1/\tau_{rise}-1/\tau_{decay})为缩放系数，建模时将其融合到参数\overline{g}中。取\tau_{rise}=2,\tau_{decay}=20，模拟代码如下：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class DualExponential(bp.dyn.TwoEndConn):
    def __init__(self, pre, post, conn, g_max=5., tau1=20.,tau2=2., delay_step=2,
                 E=0., V_rest=-65., syn_type='CUBA',method='exp_auto', **kwargs):
        super(DualExponential, self).__init__(pre=pre, post=post, conn=conn, **kwargs)
        self.tau1 = tau1
        self.tau2 = tau2
        self.g_max = g_max
        self.E = E
        self.V_rest = V_rest
        self.delay_step = delay_step
        assert syn_type in ['CUBA', 'COBA']
        self.type = syn_type
        self.pre2post = self.conn.require('pre2post')

        self.g = bm.Variable(bm.zeros(self.post.num))
        self.h = bm.Variable(bm.zeros(self.post.num))
        self.delay = bm.LengthDelay(self.pre.spike, delay_step)

        self.ini_h = bp.odeint(method=method,f=lambda h,t: -h/self.tau1)
        self.int_g = bp.odeint(method=method,f=lambda g,t,h: -g/self.tau2+h)

    def update(self, tdi):
        delayed_pre_spike = self.delay(self.delay_step)
        self.delay.update(self.pre.spike)

        post_sp = bm.pre2post_event_sum(delayed_pre_spike, self.pre2post, self.post.num, self.g_max)
        self.h.value = self.ini_h(self.h,tdi.t,tdi.dt)+post_sp
        self.g.value = self.int_g(self.g, tdi.t, self.h,tdi.dt)

        if self.type == 'CUBA':
            self.post.input += self.g * (self.E - self.V_rest)
        else:
            self.post.input += self.g * (self.E - self.post.V)


def run_syn(syn_model, title, run_duration=200., sp_times=(10, 20, 30), **kwargs):
    neu1 = bp.neurons.SpikeTimeGroup(1, times=sp_times, indices=[0] * len(sp_times))
    neu2 = bp.neurons.HH(1, V_initializer=bp.init.Constant(-50.68))
    syn1 = syn_model(neu1, neu2, conn=bp.connect.All2All(), **kwargs)
    net = bp.dyn.Network(pre=neu1, syn=syn1, post=neu2)

    # 进行模拟
    runner = bp.dyn.DSRunner(net, monitors=['pre.spike', 'post.V', 'syn.g', 'post.input'])
    runner.run(run_duration)

    # 可视化
    fig, gs = bp.visualize.get_figure(7, 1, 0.5, 6.)
    ax = fig.add_subplot(gs[0, 0])
    plt.plot(runner.mon.ts, runner.mon['pre.spike'], label='pre.spike')
    plt.legend(loc='upper right')
    plt.title(title)
    plt.xticks([])
    ax.spines['top'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['right'].set_visible(False)

    ax = fig.add_subplot(gs[1:3, 0])
    plt.plot(runner.mon.ts, runner.mon['syn.g'], label='g', color=u'#d62728')
    plt.legend(loc='upper right')
    plt.xticks([])
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax = fig.add_subplot(gs[3:5, 0])
    plt.plot(runner.mon.ts, runner.mon['post.input'], label='PSC', color=u'#d62728')
    plt.legend(loc='upper right')
    plt.xticks([])
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax = fig.add_subplot(gs[5:7, 0])
    plt.plot(runner.mon.ts, runner.mon['post.V'], label='post.V')
    plt.legend(loc='upper right')
    plt.xlabel('Time [ms]')
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    plt.show()
run_syn(DualExponential, sp_times=[25, 50, 75, 100, 160], title='Dual Exponential Model (Current-Based)', syn_type='CUBA',)
run_syn(DualExponential, sp_times=[25,50, 75, 100, 160], title='Dual Exponential Model (Conductance-Based)', syn_type='COBA',)

         在真实的生理情况下，\tau_{rise},\tau_{decay}两个参数可能相差一两个数量级，此时双指数衰减模型更加合适。而Alpha函数模型也可以看作是双指数衰减模型的一个特例。 

# python # 神经网络 # 学习
Logo
开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

第二届开放原子大赛首批创新成果集结武汉，诚邀广大开发者共鉴开源技术盛宴

第二届开放原子大赛首批创新成果集结武汉，诚邀广大开发者共鉴开源技术盛宴

avatar 开放原子开发者工作坊

诚邀报名 | 开源基础设施能力建设分论坛：打造开源生态的“心脏”

诚邀报名 | 开源基础设施能力建设分论坛：打造开源生态的“心脏”

avatar 开放原子开发者工作坊

诚邀报名 | 编程语言分论坛：AI时代的技术革新与开源实践

诚邀报名 | 编程语言分论坛：AI时代的技术革新与开源实践

avatar 开放原子开发者工作坊