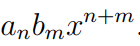
【群环域】多项式环基础
令R代表环(Ring),多项式环中x对应的系数则取自于环R,其标准的表达形式如下:假如有另外一个多项式的表达形式如下:如果两个多项式对应的系数均相等,也就是:那么则可以说两个多项式相等,也就是f(x)=g(x)。简单观察下两个多项式的系数,不难发现:以及:在多项式g(x)中,x被称之为不定项(indeterminant),是首项系数(leading coefficient),是常数项(consta
目录
一. 多项式环的基本定义
令R代表环(Ring),多项式环中x对应的系数则取自于环R,其标准的表达形式如下:
![]()
假如有另外一个多项式的表达形式如下:
![]()
如果两个多项式对应的系数均相等,也就是:
那么则可以说两个多项式相等,也就是f(x)=g(x)。
简单观察下两个多项式的系数,不难发现:
以及:
在多项式g(x)中,x被称之为不定项(indeterminant),是首项系数(leading coefficient),
是常数项(constant term)。
两个多项式可以进行基本的加法和乘法运算,如下:

综合以上,可以将该多项式环表示为R[x]。
二. 环与多项式环
多项式环的本质是一种特殊结构的环。我们知道一个数,可以看成仅有常数项的多项式,所以两者之间的关系可以用如下映射来表示:

这种映射关系,用英语可以总结为:
The zero and one elements in R[x] are the image of the zero and one element in R.
如果环R满足交换性质(commutative),那么多项式环R[x]也满足交换性质。
从多项式环中选择一个多项式f(x),如下:
由此进一步将x不断替换成环R内的元素,可以得到如下映射关系:

将a的值带入多项式,最终的结果f(a)本质也是一个环内元素。
反过来,如果将a固定,让多项式f不断变换,这个过程的本质就是将多项式环R[x]变换成环R,如下:
![]()
这个过程就是环同态(ring homomorphism)。英文的表达可能更加形象,如下:
![]()
三. 多项式环的性质
令R代表环,f代表从R[x]中抽取出的非零多项式。如果将a带入多项式中可得:
f(a)=0
首先a肯定是环R内的元素,接着a可被称之为多项式f的根(root)。
在上述环同态的运算中(),x-a则为其kernel。
将上述多项式f表示为:
![]()
在此表达式中,多项式的f的次数(degree)为n,也可以写为:
deg(f)=n
如果有一个系数满足:
那么f为首一多项式(monic)。
当然次数为0的项则为常数项。
多项式有一个特殊的性质,可以统一下。如果多项式f(x)的项全为0,可以认为此时的次数无意义,也可以认为次数是负无穷大。
四. 多项式环的次数(degree)
(1)
多项式相加不会增大次数,如下:
![]()
证明过程显然易得。
(2)
如果发现两个多项式相加的次数满足:
![]()
那么可以得出f和g的次数相等,并且他们的首项系数(leading coefficients)在环内加法运算互逆。
证明过程显然易得。
(3)
如果两个多项式的次数不相等,如下:
![]()
那么可得:
![]()
根据(2)很容易得到此处的(3)
(4)
如果环R包含所有实数,那么可得:
![]()
乘法运算的degree也满足:
deg(fg)=deg(f)+deg(g)
证明:
假定多项式f和g的degree满足:
deg(f)=n, deg(g)=m
多项式f的首项系数(leading coefficient)为,多项式g的首项系数(leading coefficient)为
。
那么很明显f和g的乘法运算fg中包含一个x指数最大的项,也就是:
![]()
再根据环R包含了所有的实数,可得:
![]()
如果环R包含所有的实数,那么多项式环R[x]也包含所有的实数多项式。同理,如果R为整环(integral),那么R[x]也为整多项式环。
如果以上定理不是整环会出现什么?
举个例子,环R=Z/15Z,很明显不是整环。给定第一个多项式:
f(x)=[1]+[3]x
以及第二个多项式:
g(x)=[2]+[5]x
首先这两个多项式肯定属于多项式环R[x]内的。并且两者的degree都为1,也就是:
deg(f)=deg(g)=1
但是两者的乘法运算会特殊一些,可以得到:
![]()
五. 多变量多项式
多项式环可以不只有一个变量,也就是:
The process of adjoining indeterminants to a ring R can be iterated to form polynomials in more than one variable with coefficients in R.
这个时候的多项式环可以表示为R[x][y],比如举一个例子,如下:
![]()
当然有的时候也可以写做R[x][y]=R[x,y]。那么,就可以引入迭代的概念:

此时的变量个数有n个,也就是:
![]()
多项式f则可以表示成:

需要强调的是,此处的求和符号一定是有限个数的。
如果从多项式中,单独抽取一项,则是单项式(monomial),也就是:
![]()
当然在密码学等实际应用的时候,R往往代表域(field)。
六. 多变量多项式环R的同态
类似单变量,多变量情况下也有同态运算的性质(evaluation homomorphism)。给定n维的环元素,如下:
![]()
那么同态映射可得:
![]()
该映射过程可以直观上看成:
![]()
其中环kernel的性质也同样适用。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献38条内容
已为社区贡献38条内容





所有评论(0)