加权kNN，k近邻算法的增强改进版本。

加权KNN算法

近邻算法（k-Nearest Neighbors, kNN）是一种用于分类和回归的非参数方法。它的基本思想是“看邻居”，即通过查找离目标点最近的 K 个数据点，来判断目标点的类别或数值。

举个例子，假设有一个训练集，其中有两类点：红色代表类别0，绿色代表类别1。现在有一个白色点，需要确定它的类别。我们选择k=3，计算白色点到所有红色点和绿色点的距离，选取距离最近的3个点。如果这3个点中有2个是绿色，1个是红色，我们就认为白色点属于绿色那一类，即类别1。

但是，KNN算法性能受到超参数k值选择的影响。如果k值过小，算法对离群点会更敏感；如果k值过大，邻域内可能包含过多来自其他类别的点。此外，考虑到一个普遍的认识，即：如果靠近的数据点之间在距离上差异很大，那么其中最靠近的那一个数据点更能可靠地表明对象的类别。 针对这一些情况，加权KNN算法随之诞生。

更直观的理解：

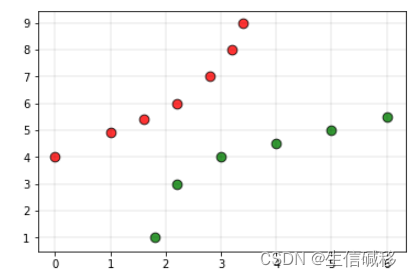
假设有以下训练集：

• 红色标签表示类别0的点，绿色标签表示类别1的点。

此时，如果我们将白色点作为查询点（需要预测类别标签的点），并且将上述数据集交给一个基于KNN的分类器，分类器会基于前面提到的最邻近原则将查询点归为类别0。但是，从图中可以明显看出，该点应该更接近类别1的点。为了克服这一缺点，我们就可以使用加权kNN。

在加权kNN中，最近的k个点根据一个称为核函数的函数赋予权重。加权kNN的直觉是，给距离较近的点更多的权重，而给距离较远的点更少的权重。任何值随距离增加而减少的函数都可以用作加权kNN分类器的核函数，其中最简单的函数是反距离函数。

反距离函数是一种常用的加权函数，用于kNN算法中，通过距离的倒数来给近邻点赋予权重。公式如下：

$$w_i=\frac{1}{d_i}$$

其中：

• $w_i$是第 $i$ 个近邻点的权重。
• $d_i$ 是第 $i$ 个近邻点到查询点的距离。

这个函数的直观理解是：距离越近的点，权重越大；距离越远的点，权重越小。这样可以更准确地反映近邻点对查询点的影响。

Python 代码实现如下：

# Python3 program to implement the 
# weighted K nearest neighbour algorithm. 

import math 

def weightedkNN(points,p,k=3): 
	''' 
	This function finds classification of p using 
	weighted k nearest neighbour algorithm. It assumes only two 
	two classes and returns 0 if p belongs to class 0, else 
	1 (belongs to class 1). 

	Parameters - 
		points : Dictionary of training points having two keys - 0 and 1 
			Each key have a list of training data points belong to that 

		p : A tuple ,test data point of form (x,y) 

		k : number of nearest neighbour to consider, default is 3 
	'''

	distance=[] 
	for group in points: 
		for feature in points[group]: 

			#calculate the euclidean distance of p from training points 
			euclidean_distance = math.sqrt((feature[0]-p[0])**2 +(feature[1]-p[1])**2) 

			# Add a tuple of form (distance,group) in the distance list 
			distance.append((euclidean_distance,group)) 

	# sort the distance list in ascending order 
	# and select first k distances 
	distance = sorted(distance)[:k] 

	freq1 = 0 # weighted sum of group 0 
	freq2 = 0 # weighted sum of group 1 

	for d in distance: 
		if d[1] == 0: 
			freq1 += (1 / d[0]) 
			
		elif d[1] == 1: 
			freq2 += (1 /d[0]) 
			

	return 0 if freq1>freq2 else 1

# Driver function 
def main(): 

	# Dictionary of training points having two keys - 0 and 1 
	# key 0 have points belong to class 0 
	# key 1 have points belong to class 1 

	points = {0:[(0, 4),(1, 4.9),(1.6, 5.4),(2.2, 6),(2.8, 7),(3.2, 8),(3.4, 9)], 
			1:[(1.8, 1),(2.2, 3),(3, 4),(4, 4.5),(5, 5),(6, 5.5)]} 

	# query point p(x,y) 
	p = (2, 4) 

	# Number of neighbours 
	k = 5

	print("The value classified to query point is: {}".format(weightedkNN(points,p,k))) 

if __name__ == '__main__': 
	main() 

参考链接：

• https://www.geeksforgeeks.org/weighted-k-nn/