【管理运筹学】第 8 章 | 动态规划(2,动态规划的基本思想与模型求解)
通过分阶段求解最短路问题,展示了动态规划方法的基本思想。
系列文章
【管理运筹学】第 8 章 | 动态规划(1,多阶段决策过程与动态规划基本概念)
【管理运筹学】第 8 章 | 动态规划(2,动态规划的基本思想与模型求解)
【管理运筹学】第 8 章 | 动态规划(3,资源分配问题)
【管理运筹学】第 8 章 | 动态规划(4,生产与储存问题)
【管理运筹学】第 8 章 | 动态规划(5,设备更新问题)
引言
承接前文,介绍完基本概念后,我们来学习动态规划的基本思想与模型求解,用上一篇文章的最短路问题来配合说明。
2.2 动态规划的基本思想
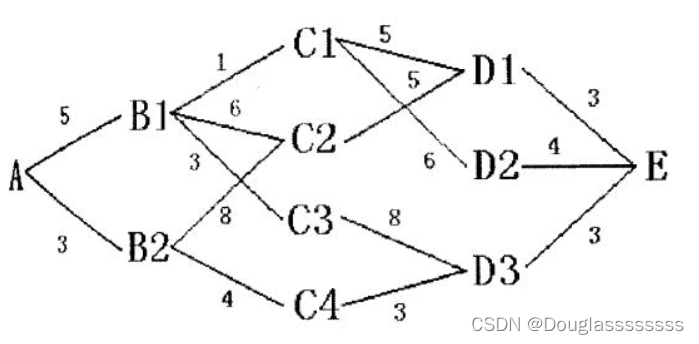
最短路问题中的网络如下图所示,从 A 到 E 可以分成 4 段,第一段从 A 到 B ,有两条路,如果选择去 B2 作为此阶段的决策,则下一阶段的起点就是 B2 ,此时又有两种选择,以此类推,可以求出一个决策序列。每一段选择不同,得到的序列便不同,我们希望求出一个最优决策,此决策对应的路线为 A 到 E 的最短路线。

显然,通过求出所有路线的距离进行比较,找出最短路对于本例是可行的,但是当路径数增加,这种穷举法的计算量会大大增加。下面介绍动态规划方法,可以帮助我们更好地求解该问题。
动态规划方法基于贝尔曼(R. Bellman)等人提出的最优化原理,这个最优化原理指出:一个过程的最优策略具有这样的性质,即无论初始状态或初始决策如何,对于先前决策所形成的状态而言,其以后的所有决策须构成最优策略。
将该原理应用到最短路问题中,即从 A 到 E 的最短路线若经过 s k s_k sk 点,则此路线由 s k s_k sk 点到 E 的部分,必是由 s k s_k sk 点到 E 点的最短路线。
如此,我们便可以从最后一个状态,即 s 4 s_4 s4 开始,向最初状态不断递推求解,最终得到从 A 到 E 的最短路线。
第一步: k = 4 k=4 k=4 ,此时状态变量集合为 S 4 = { D 1 , D 2 , D 3 } S_4=\{D1,D2,D3\} S4={D1,D2,D3} ,那么每个取值对应的指标函数分别为 f 4 ( D 1 ) = 3 , f 4 ( D 2 ) = 4 , f 4 ( D 3 ) = 3 f_4(D1)=3,f_4(D2)=4,f_4(D3)=3 f4(D1)=3,f4(D2)=4,f4(D3)=3 。
第二步: k = 3 k=3 k=3 ,此时状态变量可取值为 S 3 = { C 1 , C 2 , C 3 , C 4 } S_3=\{C1,C2,C3,C4\} S3={C1,C2,C3,C4} ,如果取 C 1 C1 C1 ,则其到终点有两条路线,需加以比较,有 f 3 ( C 1 ) = m i n { d ( C 1 , D 1 ) + f 4 ( D 1 ) d ( C 1 , D 2 ) + f 4 ( D 2 ) } = m i n { 5 + 3 6 + 4 } = 8 f_3(C1)=min\begin{Bmatrix} d(C1,D1)+f_4(D1) \\ d(C1,D2)+f_4(D2)\end{Bmatrix}=min\begin{Bmatrix} 5+3 \\ 6+4\end{Bmatrix}=8 f3(C1)=min{d(C1,D1)+f4(D1)d(C1,D2)+f4(D2)}=min{5+36+4}=8 说明从 C1 到 E 最短距离为 8 ,路径为 C 1 → D 1 → E C1\to D1 \to E C1→D1→E ,此阶段决策为 u 3 ∗ ( C 1 ) = D 1 u^*_3(C_1)=D1 u3∗(C1)=D1 。
若取 C 2 C2 C2 ,只有一条路径,即 C 2 → D 1 → E C_2\to D1\to E C2→D1→E ,则 f 3 ( C 2 ) = d ( C 2 , D 1 ) + f 4 ( D 1 ) = 8 f_3(C2)=d(C2,D1)+f_4(D1)=8 f3(C2)=d(C2,D1)+f4(D1)=8 ,相应决策为 u 3 ∗ ( C 2 ) = D 1 u^*_3(C2)=D1 u3∗(C2)=D1 。同理,可求出 f 3 ( C 3 ) = d ( C 3 , D 3 ) + f 4 ( D 3 ) = 11 , u 3 ∗ ( C 3 ) = D 3 f_3(C3)=d(C3,D3)+f_4(D3)=11,u^*_3(C3)=D3 f3(C3)=d(C3,D3)+f4(D3)=11,u3∗(C3)=D3 f 3 ( C 4 ) = d ( C 3 , D 3 ) + f 4 ( D 3 ) = 6 , u 3 ∗ ( C 4 ) = D 3 f_3(C4)=d(C3,D3)+f_4(D3)=6,u^*_3(C4)=D3 f3(C4)=d(C3,D3)+f4(D3)=6,u3∗(C4)=D3 第三步: k = 2 k=2 k=2 ,此时状态变量集合 S 2 = { B 1 , B 2 } S_2=\{B1,B2\} S2={B1,B2} ,有 f 2 ( B 1 ) = m i n { d ( B 1 , C 1 ) + f 3 ( C 1 ) d ( B 1 , C 2 ) + f 3 ( C 2 ) d ( B 1 , C 3 ) + f 3 ( C 3 ) } = m i n { 1 + 8 6 + 8 3 + 11 } = 9 , u 2 ∗ ( B 1 ) = C 1 f_2(B1)=min\begin{Bmatrix} d(B1,C1)+f_3(C1) \\ d(B1,C2)+f_3(C2) \\ d(B1,C3)+f_3(C3) \end{Bmatrix}=min\begin{Bmatrix} 1+8 \\ 6+8 \\ 3+11 \end{Bmatrix}=9,u^*_2(B1)=C1 f2(B1)=min⎩ ⎨ ⎧d(B1,C1)+f3(C1)d(B1,C2)+f3(C2)d(B1,C3)+f3(C3)⎭ ⎬ ⎫=min⎩ ⎨ ⎧1+86+83+11⎭ ⎬ ⎫=9,u2∗(B1)=C1 f 2 ( B 2 ) = m i n { d ( B 2 , C 2 ) + f 3 ( C 2 ) d ( B 2 , C 4 ) + f 3 ( C 4 ) } = m i n { 8 + 8 4 + 6 } = 10 , u 2 ∗ ( B 2 ) = C 4 f_2(B_2)=min\begin{Bmatrix} d(B2,C2)+f_3(C2) \\ d(B2,C4)+f_3(C4)\end{Bmatrix}=min\begin{Bmatrix} 8+8 \\ 4+6\end{Bmatrix}=10,u^*_2(B_2)=C4 f2(B2)=min{d(B2,C2)+f3(C2)d(B2,C4)+f3(C4)}=min{8+84+6}=10,u2∗(B2)=C4 第四步: k = 1 k=1 k=1 ,此时只有一个状态 A ,有 f 1 ( A ) = m i n { d ( A , B 1 ) + f 2 ( B 1 ) d ( A , B 2 ) + f 2 ( B 2 ) } = m i n { 5 + 9 3 + 10 } = 13 , u 1 ∗ ( A ) = B 2 f_1(A)=min\begin{Bmatrix} d(A,B1)+f_2(B1) \\ d(A,B2)+f_2(B2)\end{Bmatrix}=min\begin{Bmatrix} 5+9 \\ 3+10 \end{Bmatrix}=13,u^*_1(A)=B2 f1(A)=min{d(A,B1)+f2(B1)d(A,B2)+f2(B2)}=min{5+93+10}=13,u1∗(A)=B2 即 A 到 E 的最短距离为 13 ,按照计算顺序反推可得到最优决策序列 { u k ∗ } \{u^*_k\} {uk∗} ,为 u 1 ∗ ( A ) = B 2 , u 2 ∗ ( B 2 ) = C 4 , u 3 ∗ ( C 4 ) = D 3 , u 4 ∗ ( D 3 ) = E u^*_1(A)=B2,u^*_2(B_2)=C4,u^*_3(C4)=D3,u^*_4(D3)=E u1∗(A)=B2,u2∗(B2)=C4,u3∗(C4)=D3,u4∗(D3)=E ,则最优路线为 A → B 2 → C 4 → D 3 → E A\to B2 \to C4 \to D3 \to E A→B2→C4→D3→E 从上述求解过程中可以看出,第 k k k 阶段和第 k + 1 k+1 k+1 段都利用了如下关系 { f k ( s k ) = m i n { d k ( s k , u k ) + f k + 1 ( s k + 1 ) } , k = 4 , 3 , 2 , 1 ( 1.1 ) f 5 ( s 5 ) = 0 ( 1.2 ) \begin{cases} \ f_k(s_k)=min\{d_k(s_k,u_k)+f_{k+1}(s_{k+1})\}, & k=4,3,2,1(1.1)\\ \ f_5(s_5)=0 (1.2) \end{cases} { fk(sk)=min{dk(sk,uk)+fk+1(sk+1)}, f5(s5)=0(1.2)k=4,3,2,1(1.1) 注:状态转移方程为 s k + 1 = u k s_{k+1}=u_k sk+1=uk 。
这种递推关系称为动态规划的基本方程,式(1.2)为边界条件。
因此,可总结出动态规划方法的基本思想总结为:
- 将多阶段问题决策过程划分阶段,恰当地选取状态变量、决策变量及定义最优指标函数,从而把问题化为一族同类型的子问题,然后逐个求解。
- 求解时从最后一个阶段开始,逆方向进行,逐段递推寻优。在每个子问题求解时,都要使用它前面已经求出的子问题的最优结果,最后一个子问题的最优解就是整个问题的最优解。
- 动态规划方法是既把当前一段与未来各段分开,又把当前效益和未来效益结合起来考虑的一种最优化方法,因此每段的决策选取都是从全局考虑的,与该段的最优选择一般不同。
2.3 动态规划模型及其求解
给一个实际问题建立动态规划模型,必须做到以下 5 点。
- 将问题按时空特性恰当地划分为若干个阶段。
- 正确地规定状态变量 s k s_k sk ,使它既能描述过程的演变,又具有无后效性。
- 正确地规定决策变量 u k u_k uk 及每阶段的允许决策集合 D k ( s k ) D_k(s_k) Dk(sk) 。
- 正确地写出状态转移方程 s k + 1 = g k ( s k , u k ) s_{k+1}=g_k(s_k,u_k) sk+1=gk(sk,uk) 。
- 正确地定义各阶段的直接指标函数
d
k
(
s
k
,
u
k
)
d_k(s_k,u_k)
dk(sk,uk) 和后部子过程的最优指标函数
f
k
(
s
k
)
f_k(s_k)
fk(sk) ,并写出其基本方程:
{
f
k
(
s
k
)
=
o
p
t
u
k
∈
D
k
(
s
k
)
{
d
k
(
s
k
,
u
k
)
⊕
f
k
+
1
(
g
k
(
s
k
,
u
k
)
)
}
,
k
=
1
,
2
,
⋯
,
n
f
n
+
1
(
s
n
+
1
)
=
0
或
1
,边界条件
\begin{cases} \ f_k(s_k)=opt_{u_k\in D_k(s_k)}\{d_k(s_k,u_k)\oplus f_{k+1}(g_k(s_k,u_k))\}, & k=1,2,\cdots,n\\ \ f_{n+1}(s_{n+1})=0或1 ,边界条件 \end{cases}
{ fk(sk)=optuk∈Dk(sk){dk(sk,uk)⊕fk+1(gk(sk,uk))}, fn+1(sn+1)=0或1,边界条件k=1,2,⋯,n 其中
⊕
\oplus
⊕ 为
+
+
+ 或
×
\times
× ,当
⊕
\oplus
⊕ 为
+
+
+ 时,边界条件为 0 ;当
⊕
\oplus
⊕ 为
×
\times
× 时,边界条件为 1 。
o p t opt opt 为 min 或 max 。
以上 5 点也称为动态规划模型的 5 要素。
动态规划模型的求解,是从 k = n k=n k=n 开始,逐步向前推进,依次求解第 k k k 阶段的后部最优指标 f k ( s k ) f_k(s_k) fk(sk) 和最优子策略 p k , n ( u k ∗ , ⋯ , u n ∗ ) p_{k,n}(u_k^*,\cdots,u^*_n) pk,n(uk∗,⋯,un∗) 。当 k = 1 k=1 k=1 时,就求出了原过程的最优指标函数和最优策略。这种方法的递进求解过程和实际决策过程是相反的,故称为动态规划的逆序解法。
有些问题,也可以按照与实际决策过程相同的方向逐阶段递进,寻求最优策略,这称为动态规划的顺序解法。
当动态规划模型中的状态变量与决策变量只能取离散值时,则可采取分段穷举法,如上篇文章中的最短路问题,一般用表格形式展示。对于状态变量和决策变量取连续值时,需具体情况具体分析,灵活选取求解方法,如经典解析方法、线性规划方法、非线性规划方法和其他数值计算方法等。
下面用一个例子来说明经典解析法。
经典解析法算例
用动态规划方法求解下面的规划问题: max z = 4 x 1 + 9 x 2 + 2 x 3 2 \max{z}=4x_1+9x_2+2x_3^2 maxz=4x1+9x2+2x32 s . t . { x 1 + x 2 + x 3 = 10 x i ≥ 0 , i = 1 , 2 , 3 s.t.\begin{cases} x_1+x_2+x_3=10 \\ x_i\geq 0,i=1,2,3 \end{cases} s.t.{x1+x2+x3=10xi≥0,i=1,2,3 解: 可以将问题分为三个阶段,用每个阶段开始时的资源剩余量(约束条件即可看作资源)作为状态变量 s k s_k sk ,决策变量可取静态规划模型中的 x k ( k = 1 , 2 , 3 ) x_k(k=1,2,3) xk(k=1,2,3) 。状态转移方程为 s k + 1 = s k − x k s_{k+1}=s_k-x_k sk+1=sk−xk ,每个阶段的收益函数分别为 g 1 ( x 1 ) = 4 x 1 , g 2 ( x 2 ) = 9 x 2 , g 3 ( x 3 ) = 2 x 3 2 g_1(x_1)=4x_1,g_2(x_2)=9x_2,g_3(x_3)=2x_3^2 g1(x1)=4x1,g2(x2)=9x2,g3(x3)=2x32 。最优指标函数 f k ( s k ) f_k(s_k) fk(sk) 表示第 k k k 阶段状态为 s k s_k sk 时,从第 k k k 阶段到第 3 阶段的后部最佳收益,该问题的基本方程为 f k ( s k ) = { max { g k ( x k ) + f k + 1 ( s k − x k ) } , k = 1 , 2 , 3 f 4 ( s 4 ) = 0 f_k(s_k)=\begin{cases} \max\{g_k(x_k)+f_{k+1}(s_{k}-x_k)\},k=1,2,3 \\ f_4(s_4)=0 \end{cases} fk(sk)={max{gk(xk)+fk+1(sk−xk)},k=1,2,3f4(s4)=0 当 k = 3 k=3 k=3 时,决策变量 x 3 x_3 x3 为连续变量,取值范围为 [ 0 , s 3 ] [0,s_3] [0,s3] ,则 f 3 ( s 3 ) = max { 2 x 3 2 } f_3(s_3)=\max\{2x_3^2\} f3(s3)=max{2x32} 。这是一个一元函数求极值问题,可知当 x 3 ∗ = s 3 x^*_3=s_3 x3∗=s3 时,取得极大值 2 s 3 2 2s_3^2 2s32 ,即有 f 3 ( s 3 ) = 2 s 3 2 f_3(s_3)=2s_3^2 f3(s3)=2s32 。
当 k = 2 k=2 k=2 时,此时 x 2 ∈ [ 0 , s 2 ] x_2\in [0,s_2] x2∈[0,s2] ,则 f 2 ( s 2 ) = max { 9 x 2 + 2 s 3 2 } = max { 9 x 2 + 2 ( s 2 − x 2 ) 2 } f_2(s_2)=\max\{9x_2+2s_3^2\}=\max\{9x_2+2(s_2-x_2)^2\} f2(s2)=max{9x2+2s32}=max{9x2+2(s2−x2)2} 。记 h ( x 2 ) = 9 x 2 + 2 ( s 2 − x 2 ) 2 h(x_2)=9x_2+2(s_2-x_2)^2 h(x2)=9x2+2(s2−x2)2 ,令 d h / d x 2 = 9 − 4 ( s 2 − x 2 ) = 0 dh/dx_2=9-4(s_2-x_2)=0 dh/dx2=9−4(s2−x2)=0 ,得 x 2 = s 2 − 9 / 4 x_2=s_2-9/4 x2=s2−9/4 ;又由 d 2 h / d x 2 2 = 4 > 0 d^2h/dx_2^2=4>0 d2h/dx22=4>0 ,故 x 2 = s 2 − 9 / 4 x_2=s_2-9/4 x2=s2−9/4 为极小值点,极大值在端点处取得。
h ( 0 ) = 2 s 2 2 , h ( s 2 ) = 9 s 2 h(0)=2s_2^2,h(s_2)=9s_2 h(0)=2s22,h(s2)=9s2 ,当 2 s 2 2 ≥ 9 s 2 2s_2^2 \geq 9s_2 2s22≥9s2 ,即 s 2 ≥ 9 / 2 s_2\geq9/2 s2≥9/2 时, x 2 ∗ = 0 x_2^*=0 x2∗=0 ;当 s 2 < 9 / 2 s_2<9/2 s2<9/2 时, x 2 ∗ = s 2 x^*_2=s_2 x2∗=s2 。
当 k = 1 k=1 k=1 时, s 1 = 10 , x 1 ∈ [ 0 , 10 ] s_1=10,x_1\in [0,10] s1=10,x1∈[0,10] 。若当 s 2 < 9 / 2 s_2<9/2 s2<9/2 时, f 2 ( s 2 ) = 9 s 2 f_2(s_2)=9s_2 f2(s2)=9s2 ,有 f 1 ( s 1 ) = max { 4 x 1 + 9 ( 10 − x 1 ) } = max { 90 − 5 x 1 } f_1(s_1)=\max\{4x_1+9(10-x_1)\}=\max\{90-5x_1\} f1(s1)=max{4x1+9(10−x1)}=max{90−5x1} ,则 x 1 ∗ = 0 x^*_1=0 x1∗=0 ,此时 s 2 = 10 > 9 / 2 s_2=10>9/2 s2=10>9/2 ,与条件矛盾,故舍去。
则 f 2 ( s 2 ) = 2 s 2 2 , f 1 ( s 1 ) = max { 4 x 1 + 2 ( 10 − x 1 ) 2 } f_2(s_2)=2s_2^2,f_1(s_1)=\max\{4x_1+2(10-x_1)^2\} f2(s2)=2s22,f1(s1)=max{4x1+2(10−x1)2} 。记 u ( x 1 ) = 4 x 1 + 2 ( 10 − x 1 ) 2 u(x_1)=4x_1+2(10-x_1)^2 u(x1)=4x1+2(10−x1)2 ,令 d u / d x 1 = 4 − ( 10 − x 1 ) = 0 du/dx_1=4-(10-x_1)=0 du/dx1=4−(10−x1)=0 ,得 x 1 = 9 x_1=9 x1=9 ,此时 d 2 u / d x 1 2 = 1 > 0 d^2u/dx_1^2=1>0 d2u/dx12=1>0 ,故其为极小值点。应在端点处取极大值,有 u ( 0 ) = 200 , u ( 10 ) = 40 < 200 u(0)=200,u(10)=40<200 u(0)=200,u(10)=40<200 ,故 x 1 ∗ = 0 x_1^*=0 x1∗=0 。
由转移方程进行回推,有 s 2 = 10 , x 2 ∗ = 0 ; s 3 = 10 , x 3 ∗ = s 3 = 10 s_2=10,x_2^*=0;s_3=10,x_3^*=s_3=10 s2=10,x2∗=0;s3=10,x3∗=s3=10 ,故原问题最优解为 ( 0 , 0 , 10 ) T (0,0,10)^T (0,0,10)T ,最优解值为 200 。
写在最后
那么以上就是动态规划的基本内容了,往后,我们将针对具体类型的问题来深入进行理解,包括资源分配、生产与储存和设备更新问题。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献21条内容
已为社区贡献21条内容





所有评论(0)