目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

       有限差分是形式为f(x+b)-f(x+a)的数学表达式。如果有限差分除以b-a，则得到差商。 有限差分导数的逼近在微分方程数值解的有限差分方法，特别是边界值问题，起着关键的作用。有限差分是形式为f(x+b)-f(x+a)的数学表达式。如果有限差分除以b-a，则得到差商。 有限差分导数的逼近在微分方程数值解的有限差分方法，特别是边界值问题，起着关键的作用。

       简称差分法或网格法，是求微分方程和积分一微分方程的数值解的一种主要的计算方法。它的基本思想是：把连续的定解区域用由有限个离散点构成的网格来代替，这些离散点被称为网格的结(节)点;把在连续定解区域上定义的连续变量函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似，积分用积分和来近似。于是原方程和定解条件就可用代数方程组来近似地代替，解此代数方程组就得到原问题的近似解。这种方法简单、通用，易于在电子计算机上实现。
      有限差分方法有漫长的历史，源于牛顿、欧拉等人的工作，他们曾用差商代替微商以简化计算。1928年，库朗、卢伊等人证明了三大典型方程的典型差分格式的收敛性定理，为现代有限差分理论提供了基础。同时，库朗把有限差分法用于求偏微分方程的数值解，发展了这一方法。由于有限差分方法具有通用性，又便于机器实现，因而在电子计算机产生和广泛应用后更得到很大发展及更广泛的应用。冯 ·诺伊曼于1948年对无粘流体(非线性双曲型)方程提出的引入人工粘性项的差分方法是一个典型例子，他还同时提出计算稳定性概念和线性化傅立叶方法来分析稳定性。后来拉克斯等人建立了一般差分格式的收敛性、稳定性等价定理。人工粘性法成为现代流体计算的主导方法之一，而得出这种方法的自适应的算法思想也给其他计算方法的发展以很大的启发和影响。在现代，有限差分方法应用于各类微分方程和积分—微分方程的各种定解问题，如常微分方程初值问题、边值问题，偏微分方程初值问题、边值问题，玻耳兹曼方程，计算流体力学等等。它是把微分方程离散化，从而求其数值解的基本方法之一。

       有限差分法是一种数值方法，用于求解微分方程的近似解。该方法通过将连续的时间或空间离散化，将微分方程转化为差分方程，然后求解差分方程得到原微分方程的近似解。下面介绍有限差分法的基本原理和数学公式。
假设要求解一个一阶微分方程
y'(t) = f(t, y)
y(t0) = y0
其中 y(t) 是待求函数，f(t, y) 是已知函数，y0 是已知的初始值。
将时间区间 [t0, tf] 离散化，分成 N 个小区间，每个小区间的长度为 h，即
[t0, tf] = [t0, t0+h, t0+2h, ..., tf]
在每个小区间上，微分方程可以近似为
y'(t) ≈ h^{-1}(y(t+h) - y(t))
f(t, y) ≈ f(t, y(t))
因此，在每个小区间上，原微分方程可以近似为
h^{-1}(y(t+h) - y(t)) = f(t, y(t))
整理得到差分方程
y(t+h) = y(t) + h f(t, y(t))
这就是在每个小区间上的差分方程。
对于第一个小区间 [t0, t0+h]，由于 y(t0) 已知，因此可以作为边界条件。对于后面的小区间，可以通过前一个小区间的差分方程得到。因此，可以通过迭代的方式求解整个时间区间上的差分方程，得到原微分方程的近似解。
下面是一个简单的例子，用有限差分法求解一维热传导方程
∂u/∂t = α (∂²u/∂x²)
其中 u(x, t) 是待求函数，α 是常数。
将时间区间 [0, T] 离散化，分成 N 个小区间，每个小区间的长度为 h，即
[0, T] = [0, h, 2h, ..., Nh]
将空间区间 [a, b] 离散化，分成 M 个小区间，每个小区间的长度为 δx，即
[a, b] = [a, a+δx, a+2δx, ..., b]
在每个小区间上，将偏导数用中心差分近似为
∂u/∂x ≈ (u(x+δx) - u(x-δx))/2δx
∂²u/∂x² ≈ (u(x+δx) - 2u(x) + u(x-δx))/δx²
因此，在每个小区间上，原微分方程可以近似为
du/dt = α (u(x+δx) - 2u(x) + u(x-δx))/(δx²)
整理得到差分方程
u(x, t+h) = u(x, t) + h α (u(x+δx, t) - 2u(x, t) + u(x-δx, t))/(δx²)
这就是在每个小区间上的差分方程。
对于第一个小区间 [0, h]，由于 u(x, 0) 已知，因此可以作为边界条件。对于后面的小区间，可以通过前一个小区间的差分方程得到。因此，可以通过迭代的方式求解整个时间区间上的差分方程，得到原微分方程的近似解。

---

这里，以如下的方程组为例子：

用MATLAB有限差分求上式的数值解。

求解过程如下：

首先将上面的式子简化，获得如下的式子：

 

进一步转换： 

 

 进一步转换：

上面的式子可以改为： 

然后再计算循环过程中，取 

然后做转换，得到：

二、核心程序

.................................................
maxt   = 1;
k      = 0;
t      = 0;
h      = 5e-7;   
while(maxt > 1e-5 & k < 2000)
      k
      k    = k + 1;
      maxt = 0;
      for i=2:1:999
          A        = k33 + (k11-k33)*cos(f1(i-1))^2; 
          B        = 0.5*(k11-k33)*sin(2*f1(i-1));
          C        = 0.5*deltae*E*E*sin(2*f1(i-1));
          f2(i+1)  =(B*(f1(i) - f1(i-1))^2 - h^2*C)/A + 2*f1(i) - f1(i-1);
          t        = abs(f2(i+1) - f1(i));
          if t > maxt
             maxt = t;
          end
      end
      f1  = f2; 
end
 
...............................................

while(maxt > 1e-5 & k < 2000)
      k
      k    = k + 1;
      maxt = 0;
      for z=2:1:999
          E(z)     = 0.08*(3.283e13*z^3 - 2.234e9*z^2 - 5.875e7*z + 2.737e5);
          A        = k33 + (k11-k33)*cos(f1(z-1))^2; 
          B        = 0.5*(k11-k33)*sin(2*f1(z-1));
          C        = 0.5*deltae*E(z)*E(z)*sin(2*f1(z-1));
          f2(z+1)  =(B*(f1(z) - f1(z-1))^2 - h^2*C)/A + 2*f1(z) - f1(z-1);
          t        = abs(f2(z+1) - f1(z));
          if t > maxt
             maxt = t;
          end
      end
      f1  = f2; 
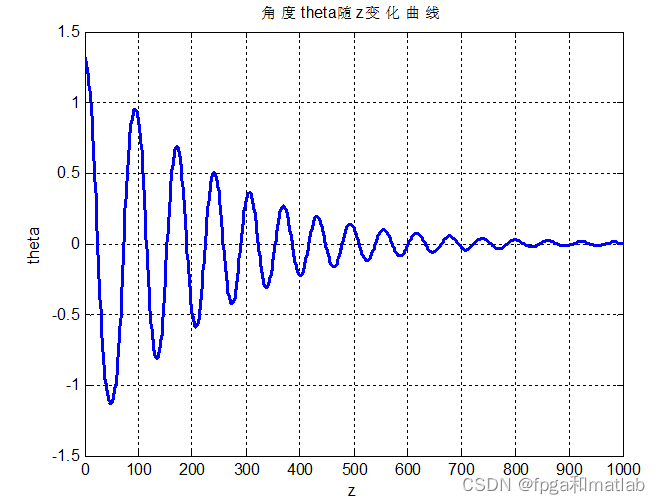
end

三、测试结果

 A16-35