栅格地图建立-Grid-Mapping
占栅格地图-Occupancy Grid Map,理论推导及代码阅读。
0.引言
本文只是根据资料自己学习的过程记录。主要参考的资料有:
问题:给定机器人的位姿和传感器的观测数据(主要指激光雷达)。
data
=
{
x
1
,
z
1
,
x
2
,
z
2
,
⋯
x
n
,
z
n
}
\text { data }=\left\{x_{1}, z_{1}, x_{2}, z_{2}, \cdots x_{n}, z_{n}\right\}
data ={x1,z1,x2,z2,⋯xn,zn}
求解:最可能的地图。
m
∗
=
arg
max
m
P
(
m
∣
x
1
:
t
,
z
1
:
t
)
m^{*}=\arg \max _{m} P\left(m \mid x_{1: t}, z_{1: t}\right)
m∗=argmmaxP(m∣x1:t,z1:t)
// 初始位置
int size_x_, size_y_, init_x_, init_y_;
// 地图分辨率
double cell_size_;
// 整个地图, 初始化概率全为 0.5 (unknown)
Eigen::MatrixXd bel_data_;

void GridMap::toRosOccGridMap( const std::string& frame_id, nav_msgs::OccupancyGrid& occ_grid)
{
occ_grid.header.frame_id = frame_id;
occ_grid.header.stamp = ros::Time::now();
occ_grid.info.width = size_x_;
occ_grid.info.height = size_y_;
occ_grid.info.resolution = cell_size_;
occ_grid.info.origin.position.x = -init_x_*cell_size_;
occ_grid.info.origin.position.y = -init_y_*cell_size_;
// 没有赋值旋转
// # The map data, in row-major order, starting with (0,0). Occupancy
// # probabilities are in the range [0,100]. Unknown is -1.
const int N = size_x_ * size_y_;
for(size_t i= 0; i < N; i ++)
{
double& value = bel_data_.data()[i];
if(value == 0.5)
occ_grid.data.push_back( -1);
else
occ_grid.data.push_back( value * 100);
}
}
1.建图前提假设
-
(1)栅格地图中的栅格是一个二元随机变量,只能取两个值:占用(Occupied)或者空闲(Free)。 𝑝 ( m i ) = 1 𝑝(m_i) = 1 p(mi)=1 表示被占用, 𝑝 ( m i ) = 0 𝑝(m_i) = 0 p(mi)=0 表示空闲, 𝑝 ( m i ) = 0.5 𝑝(m_i) = 0.5 p(mi)=0.5 表示未知(Unknown)
-
(2)在建图的过程中,环境不会发生改变。
-
(3)地图中的每一个栅格都是独立的,因此数学表达式可以表示为:
p ( m ) = ∏ p ( m i ) \mathrm{p}(m)=\prod p\left(m_{i}\right) p(m)=∏p(mi)地图估计问题即可表示为:
p ( m ∣ x 1 : t , z 1 : t ) = ∏ p ( m i ∣ x 1 : t , z 1 : t ) \mathrm{p}\left(m \mid x_{1: t}, z_{1: t}\right)=\prod p\left(m_{i} \mid x_{1: t}, z_{1: t}\right) p(m∣x1:t,z1:t)=∏p(mi∣x1:t,z1:t)因此,估计环境的地图只需要对每一个独立的栅格进行估计即可。
2.建图推导


最后推导的结果为:
l ( m i ∣ x 1 : t , z 1 : t ) = l ( m i ∣ x t , z t ) + l ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) − l ( m i ) l\left(m_{i} \mid x_{1: t}, z_{1: t}\right)=l\left(m_{i} \mid x_{t}, z_{t}\right)+l\left(m_{i} \mid x_{1: t-1}, z_{1: t-1}\right)-l\left(m_{i}\right) l(mi∣x1:t,z1:t)=l(mi∣xt,zt)+l(mi∣x1:t−1,z1:t−1)−l(mi)
- l ( m i ∣ x 1 : t , z 1 : t ) l\left(m_{i} \mid x_{1: t}, z_{1: t}\right) l(mi∣x1:t,z1:t)表示激光雷达的逆观测模型(inverse measurement Model), 未知。
- l ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) l\left(m_{i} \mid x_{1: t-1}, z_{1: t-1}\right) l(mi∣x1:t−1,z1:t−1) 表示栅格 𝑚 𝑖 𝑚_𝑖 mi在 t − 1 t-1 t−1时刻的状态,递归项,已知。
- l ( m i ) l\left(m_{i}\right) l(mi) 表示栅格𝑚𝑖的先验值,该值对所有栅格都相同,初始化给定,已知。
或者表达为:
l
t
,
i
=
i
n
v
_
s
e
n
s
o
r
_
m
o
d
e
l
(
m
i
,
x
t
,
z
t
)
+
l
t
−
1
,
i
−
l
0
l_{t, i}= inv\_sensor\_model \left(m_{i}, x_{t}, z_{t}\right)+l_{t-1, i}-l_{0}
lt,i=inv_sensor_model(mi,xt,zt)+lt−1,i−l0
-
l t , i = log b e l t ( m i ) 1 − b e l t ( m i ) = log p ( m i ∣ z 1 : t , x 1 : t ) 1 − p ( m i ∣ z 1 : t , x 1 : t ) l_{t, i}=\log \frac{b e l_{t}\left(m_{i}\right)}{1-b e l_{t}\left(m_{i}\right)}=\log \frac{p\left(m_{i} \mid z_{1: t}, x_{1: t}\right)}{1-p\left(m_{i} \mid z_{1: t}, x_{1: t}\right)} lt,i=log1−belt(mi)belt(mi)=log1−p(mi∣z1:t,x1:t)p(mi∣z1:t,x1:t) 未知。
-
l i n v , i = log p ( m i ∣ z t , x t ) 1 − p ( m i ∣ z t , x t ) l_{i n v, i}=\log \frac{p\left(m_{i} \mid z_{t}, x_{t}\right)}{1-p\left(m_{i} \mid z_{t}, x_{t}\right)} linv,i=log1−p(mi∣zt,xt)p(mi∣zt,xt) 递归项,已知。
-
l 0 = log p ( m i ) 1 − p ( m i ) l_{0}=\log \frac{p\left(m_{i}\right)}{1-p\left(m_{i}\right)} l0=log1−p(mi)p(mi) 初始化给定,已知。
因此,此时唯一需要求解的就是 l ( m i ∣ x 1 : t , z 1 : t ) l\left(m_{i} \mid x_{1: t}, z_{1: t}\right) l(mi∣x1:t,z1:t) 逆观测模型。一个后验估计,推导成这么简洁的式子,妙。
3.逆观测模型




后三个图,结合第一个图理解,后三个图依次从“free”、“occ”、“no ifo”,对应的就是图一中的击中过程,概率分别应该是0、1、0.5. 应该是为了理解,后面三张图进行了夸大绘制。

这个图更好理解一点。 z t , n z_{t,n} zt,n 为 t 时刻的第 n 束激光, r r r 就是小格子的长度,分辨率。最后将概率值经过 l t , i = log b e l t ( m i ) 1 − b e l t ( m i ) = log p ( m i ∣ z 1 : t , x 1 : t ) 1 − p ( m i ∣ z 1 : t , x 1 : t ) l_{t, i}=\log \frac{b e l_{t}\left(m_{i}\right)}{1-b e l_{t}\left(m_{i}\right)}=\log \frac{p\left(m_{i} \mid z_{1: t}, x_{1: t}\right)}{1-p\left(m_{i} \mid z_{1: t}, x_{1: t}\right)} lt,i=log1−belt(mi)belt(mi)=log1−p(mi∣z1:t,x1:t)p(mi∣z1:t,x1:t) 即完成了逆测量模型项的计算。
至此, l ( m i ∣ z t , x t ) l\left(m_{i} \mid z_{t}, x_{t}\right) l(mi∣zt,xt) 也求解完毕.
/*
注意参数,和推导有所区别:
sensor_model:
P_occ: 0.6
P_free: 0.4
P_prior: 0.5
*/
double GridMapper::laserInvModel ( const double& r, const double& R, const double& cell_size )
{
if(r < ( R - 0.5*cell_size) )
return P_free_; // 障碍物前面 free 0.4
if(r > ( R + 0.5*cell_size) )
return P_prior_; // 障碍物后面 unknown 0.5
return P_occ_; // 障碍物 occupancy 0.6
}
4.Occupancy Mapping Algorithm
完整的算法流程如图:

LaserScan:
std_msgs/Header header // 数据的消息头
uint32 seq // 数据的序号
time stamp // 数据的时间戳
string frame_id // 数据的坐标系
float32 angle_min // 雷达数据的起始角度(最小角度)
float32 angle_max // 雷达数据的终止角度(最大角度)
float32 angle_increment // 雷达数据的角度分辨率(角度增量)
float32 time_increment // 雷达数据每个数据点的时间间隔
float32 scan_time // 当前帧数据与下一帧数据的时间间隔
float32 range_min // 雷达数据的最小值
float32 range_max // 雷达数据的最大值
float32[] ranges // 雷达数据每个点对应的在极坐标系下的距离值
float32[] intensities // 雷达数据每个点对应的强度值
雷达坐标系转odom坐标系:
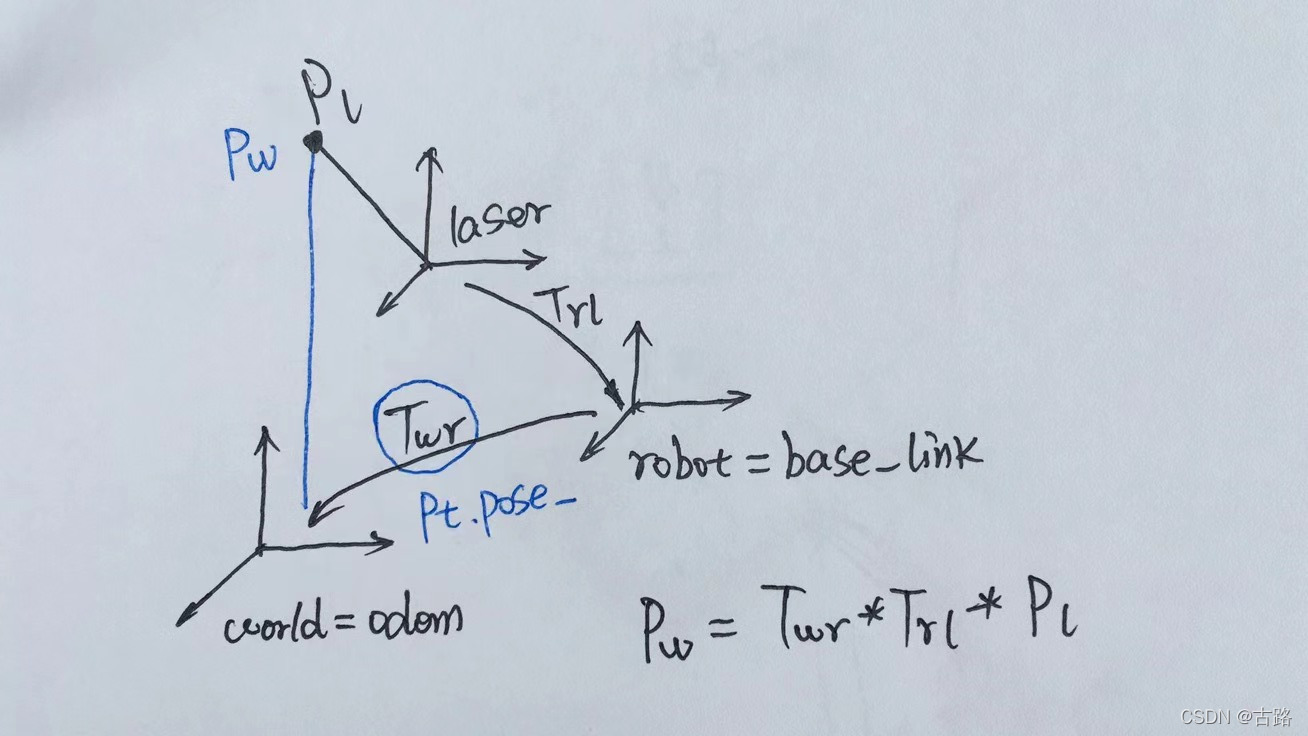
void GridMapper::updateMap ( const sensor_msgs::LaserScanConstPtr& scan, Pose2d& robot_pose )
{
/* 获取激光的信息 */
const double& ang_min = scan->angle_min;
const double& ang_max = scan->angle_max;
const double& ang_inc = scan->angle_increment;
const double& range_max = scan->range_max;
const double& range_min = scan->range_min;
/* 设置遍历的步长,沿着一条激光线遍历 */
const double& cell_size = map_->getCellSize();
const double inc_step = 1.0 * cell_size; // 一个格子一个格子的计算
/* for every laser beam */
for(size_t i = 0; i < scan->ranges.size(); i ++)
{
/* 获取当前beam的距离 */
double R = scan->ranges.at(i);
if(R > range_max || R < range_min)
continue;
/* 沿着激光射线以inc_step步进,更新地图*/
double angle = ang_inc * i + ang_min;
double cangle = cos(angle);
double sangle = sin(angle);
Eigen::Vector2d last_grid(Eigen::Infinity, Eigen::Infinity); //上一步更新的grid位置,防止重复更新
for(double r = 0; r < R + cell_size; r += inc_step)
{
Eigen::Vector2d p_l(
r * cangle,
r * sangle
); //在激光雷达坐标系下的坐标
/* 转换到世界坐标系下 */
Pose2d laser_pose = robot_pose * T_r_l_;
Eigen::Vector2d p_w = laser_pose * p_l;
/* 更新这个grid */
if(p_w == last_grid) //避免重复更新
continue;
updateGrid(p_w, laserInvModel(r, R, cell_size));
last_grid = p_w;
}//for each step
}// for each beam
}
/**
* @description: 一个格子一个格子的更新 概率值
* @param {Vector2d&} grid 格子坐标
* @param {double&} pmzx 逆观测模型
*/
void GridMapper::updateGrid ( const Eigen::Vector2d& grid, const double& pmzx )
{
/* TODO 这个过程写的太低效了 */
double log_bel; // 递归项 + 先验项 都在里面
if( ! map_->getGridLogBel( grid(0), grid(1), log_bel ) ) //获取log的bel
return;
log_bel += log( pmzx / (1.0 - pmzx) ); // 更新 ? 逆观测模型值为 1 怎么办 A:注意参数,和推导有所区别
map_->setGridLogBel( grid(0), grid(1), log_bel ); //设置回地图
}
5.demo
我这边跑出来,里程计飘了是怎么回事。
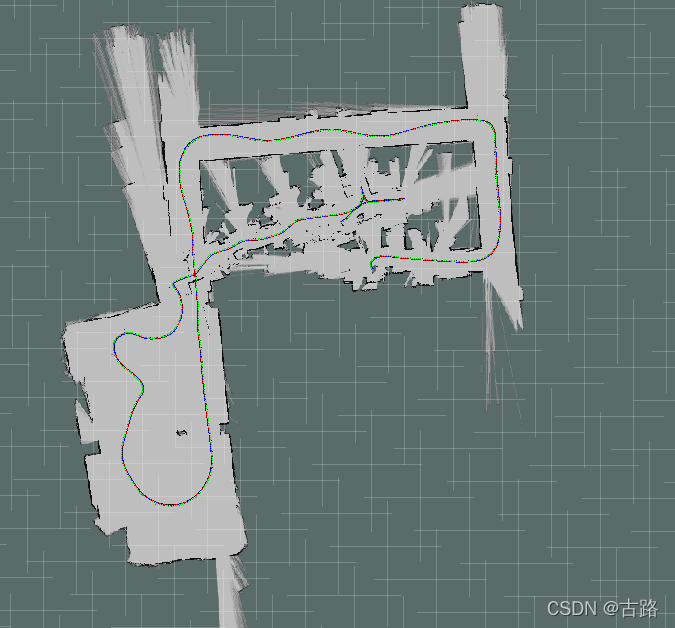

上一次跑粒子滤波定位,里程计也是飘的,参考博客。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容





所有评论(0)