1 概述

1.1 论文题目

通过学习基函数的小样本回归(Few-Shot Regression Via Learned Basis Functions)

1.2 摘要

  近来，小样本学习算法使模型能够在仅有的几个训练样本的基础上快速适应新任务。以前的小样本学习内容主要集中在分类和强化学习上。在本文中，我们提出了一种专门针对回归任务的小样本元学习系统。我们的模型是基于这样的想法：如果未知函数被表示为一组适当的基础函数的线性组合，那么它的自由度就可以大大降低。这使得少数标记的样本就能近似于该函数。我们设计了一个特征提取器网络(Feature Extractor network) 来编码任务分布的基础函数，以及权重生成器(Weights Generator) 来生成新任务的权重向量。我们表明，我们的模型在各种回归任务中的表现优于目前最先进的元学习方法。

2 研究内容

2.1 简介

  回归处理的是学习一组输入与一组输出之间的模型问题。学习的模型可以被认为是函数 $y=F(x)$ ，它将给出一个预测 $y\in R^{d_y}$，给定输入$x\in R^{d_x}$，其中$d_y$和$d_x$分别是输出和输入的尺寸。通常情况下，回归模型是在大量的数据点上训练出来的，以便能够对新的输入进行准确预测。最近，关于小样本学习方法的有了很大的发展 (Vinyals et al.,2016; Koch et al., 2015; Gidaris & Komodakis, 2018)。 小样本学习方法只需要每个任务中的几个例子，就能够迅速适应并在新任务中表现良好。小样本学习模型实质上是学会学习，即模型学会了快速适应新的任务，而不仅仅是学会对特定的输入样本作出正确的预测。

  在这项工作中，我们提出了一个针对小样本回归任务的小样本学习模型。我们在正弦波回归任务上评估了我们的模型，并将我们的模型的性能与几种元学习算法进行了比较。 我们进一步介绍了另外两个回归任务，即由偏微分方程建模的一维热方程任务和二维高斯分布任务。

2.2 相关的工作

  回归问题长期以来一直是机器学习和信号处理界的一个研究主题(Myers & Myers, 1990; Specht, 1991)。虽然回归与分类类似，但回归估计的是一个或多个标量值，通常被认为是一个单一任务问题。 我们的模型反而将回归问题重新表述为一个小样本学习问题，使我们的模型能够对从同一任务分布中采样的任务进行回归。

  元学习的问题同样也是一般机器学习界长期关注的话题 (Thrun & Pratt, 1998; Schmidhuber, 1987; Naik & Mammone, 1992)。元学习已被应用于小样本学习问题，它关注的是能从先前经验中学习以适应新任务的模型。 Lake等人（2011年）在2011年首次提出了单次分类问题，并引入了Omniglot数据集，作为一个类似于MNIST数据集（LeCun，1998）的传统分类的小样本分类数据集。 从那时起，就涌现了大量的小样本学习方法（Vinyals等人，2016；Finn等人，2017；Gidaris & Komodakis，2018；Rusu等人，2018），但其中大部分都集中在小样本分类和强化学习领域。

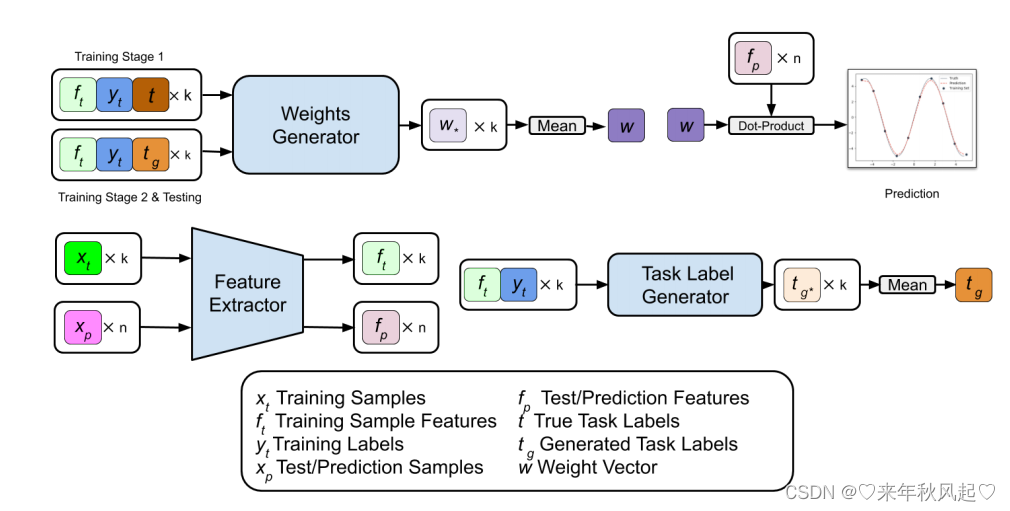
  图1：模型概览。请注意，在元训练期间，我们使用回归任务的真实任务标签作为权重发生器的输入，以训练权重发生器和特征提取器，而任务标签发生器生成的任务标签只在元测试期间使用。

3. 通过学习基函数的小样本回归

  我们首先讨论我们的想法。我们的目标是开发一个能够迅速适应回归一个新函数的模型，该模型仅基于该函数的几个样本。具体来说，我们希望对未知函数 $y=F(x)$ 进行建模，只给 $D_{train}$ = $\{(x^k,y^k)|k=\mathrm{1...}K\}$ 。对于小的 K，例如$K=10$，这是一个棘手的任务，因为F(x)可以采取任何形式。我们遵循常见的设置：我们假设我们想回归的每个函数是一个从未知分布 $p(T)$ 中抽取的任务 $T_i$。

  为了简化讨论，我们假设标量输入和标量输出。我们的想法是学习未知函数 $F(x)$ 的稀疏或可压缩表示，以便少数样本 $\{(x^k,y^k)|k=\mathrm{1...}K\}$ 可以提供足够的信息来估计$F(x)$。具体来说，我们将未知函数$F(x)$建模为一组基础函数 { ϕ i ( x ) } \{\phi_i(x)\} {ϕi​(x)}的线性组合。

$$F(x)=\sum _i{w}_i{\varphi }_i(x)\text{\hspace{1em}(1)}$$

  已经开发了许多基函数来扩展 $F(x)$ 。例如，麦克劳林数列展开（$x=0$时的泰勒数列展开）使用 { ϕ i ( x ) } = { 1 , x , x 2 , x 3 , . . . } \{\phi_i(x)\}=\{1, x, x^2 , x^3 , ...\} {ϕi​(x)}={1,x,x2,x3,...} :

$$F(x)=w_0+w_{1}x+w_2{x}^2+...\text{\hspace{1em}(2)}$$

  如果 $F(x)$ 是一个多项式，(2) 可以是一个可压缩的表示，即只有几个非零/重要的 $w_i$ 。 然而，如果F(x)是一个正弦波，就需要很多项来充分表示F(x)，例如：

$$sin(x)\approx w_{1}x+w_3{x}^3+w_5{x}^5+w_7{x}^7+...+w_M{x}^M\text{\hspace{1em}(3)}$$

  在（3）中，M 是大的，并且 $M\gg K$ 。 只给定 $K$ 个样本 $\{(x^k,y^k)|k=\mathrm{1...}K\}$ ，就不足以来确定 { w i } \{w_i\} {wi​} 和对未知函数进行建模。另一方面，如果我们用傅里叶基代替 ，即 { ϕ i ( x ) } = { 1 , s i n ( x ) , s i n ( 2 x ) , . . . , c o s ( x ) , c o s ( 2 x ) , . . . } \{\phi_i(x)\} = \{1, sin(x), sin(2x), ... , cos(x), cos(2x), ...\} {ϕi​(x)}={1,sin(x),sin(2x),...,cos(x),cos(2x),...} ，显然，我们可以得到一个稀疏的表示：我们可以只用几个项表示一个正弦体。在傅里叶基础下，只有几个非零线性权重 $w_i$，$K$个样本足以估计$w_i$并估计函数。本质上，有了适当的 { ϕ i ( x ) } \{\phi_i(x)\} {ϕi​(x)}，用(1)建模时，$F(x)$ 的自由度可以大大降低，因此，$K$样本可以很好地估计 $F(x)$。

  我们的方法是利用从 $p(T)$ 中抽取的训练任务集来学习 { ϕ i ( x ) } \{\phi_i(x)\} {ϕi​(x)} ，从而对从 $p(T)$ 中抽取的任何任务形成稀疏或可压缩表示。 { ϕ i ( x ) } \{\phi_i(x)\} {ϕi​(x)} 的集合被编码在 特征提取器(Feature Extractor) 中，该提取器接收 $x$ 并输出 $\Phi (x)=[{\varphi }_1(x),{\varphi }_2(x),...,{\varphi }_M(x){]}^T$。在我们的框架中，$\Phi (x)$对于从$p(T)$中抽取的任何任务都是一样的，因为它编码了可以稀疏地表示 $p(T)$ 中任何任务的 { ϕ i ( x ) } \{\phi_i(x)\} {ϕi​(x)} 的集合。我们进一步学习权重发生器(Weights Generator) ，将一个新任务的 $K$ 个训练样本映射到一个常数向量 $w=[w_1,w_2,...,w_M{]}^T$ 。未知函数被建模为 $w^T\Phi (x)$ 。

3.1 模型结构

  在此，我们详细介绍一下我们的小样本回归模型。给定一个回归任务 $T$，$D_{train}=\{(x^k,y^k)|k=\mathrm{1...}K\}$，模型的任务是在一个数值范围内预测整个回归函数。

  训练样本 $x\in R^{d_x}$，首先通过特征提取器被表示为一个函数 ，$F(x|{\theta }^F)$，具有可训练的参数${\theta }^F$。特征提取器输出一个高维的特征表示，$f\in R^{d_f}$ ，其中$d_f$是特征表示的维度，对于每个 任务 $T$ 的训练点。请注意，$d_f$ 是编码在特征提取器中的基函数的数量。

  特征表示 $x_f$，连同标签 $y\in R^{d_y}$ 和任务标签 $t\in R^{d_t}$ 由任务标签生成器生成，然后通过权重生成器。权重发生器表示为一个函数 $G(f,y,t|{\theta }^G)$，具有可训练的参数 ${\theta }^G$ ，为回归任务的每个训练样本输出一个权重向量 $w_k$ 。任务 $T$ 的最终权重向量 $w_0$ 是通过取 $k$ 个权重向量的平均值得到的。权重生成器本身由Vaswani等人（2017）引入的一系列具有缩放点积注意力(scaled dot product attention) 学习链接1 的 自注意力模块(self-attention modules) 学习链接2 组成。每个自注意力模块都允许权重生成器 "查看 "权重生成器输入的嵌入，让生成器 "选择 "嵌入中最有助于为每个训练样本生成最佳权重的部分。

  然后，该模型能够对任务 $T$ 的点集 D p r e d = { x n ∣ n = 1... N } D_{pred} = \{x^n|n = 1...N\} Dpred​={xn∣n=1...N} 进行预测，方法是在特定任务的权重向量 $w$ 和预测集的特征表示之间取点积。

$$y^{\prime }=w^{T}F(x\in D_{pred}|{\theta }^F)\text{\hspace{1em}(4)}$$

  请注意，在我们所有的回归实验中，$y$ 的维度为1。然而，我们的模型能够通过从权重发生器输出 $d_y$ 权重向量来预测更高维度的 $y$ 的回归任务，预测结果可以通过在 $y$ 的每个维度上对单个权重向量和 $f$ 进行点乘来获得。我们的模型的概述可以在图1中找到。

3.2 任务标签生成器

  在样本层面上的标签信息之外，与其他小样本学习任务不同，小样本回归任务在任务层面上也拥有额外的标签信息。这些任务层的标签是描述回归函数的参数，我们可以利用它来提高小样本回归模型的性能。 例如，一个正弦波函数有参数标签，如振幅、相位和频率。我们把这些任务层的标签称为任务标签，$t$ ，并把它作为权重发生器的额外输入。

  尽管我们假设模型在训练阶段可以获得任务标签，但假设此类信息在测试期间也可用或可靠是不现实的。因此，我们引入任务标签生成器作为模型的附加组件。我们将其表示为具有可训练参数 ${\theta }^T$ 的函数 $T(x_f,y|{\theta }^T)$ 。它接受回归任务 $T$ 的特征表示 $x_f$ 和标签 $y$ ，并尝试为 $T$ 输出正确的任务标签 $t_g$ 。与权重生成器类似，我们还使用任务标签生成器中的自注意力模块，使任务标签生成器能够“查看”输入中对生成正确任务标签最有用的部分。

  表1：比较MAML和我们的模型在不同回归任务上的均方误差。越低越好。

  表2：添加任务标签效果的实验

4. 结果与评估

  我们在三个小样本回归任务上评估我们的模型。第一个任务是正弦回归任务，在最近的小样本学习论文中已经使用过(Finn等人，2017；Rusu等人，2018；Li等人，2017)。我们还引入了另外两个回归任务，即一维热方程任务(Cannon, 1984)和高维二维高斯分布任务。对于正弦波任务，我们将我们的模型与Li等人（2017）提出的Meta-SGD进行比较。我们还将我们在正弦任务上的结果与Yoon等人（2018）的结果进行了比较，他们在正弦任务上添加了一个噪声成分，仅使用有限数量的任务进行训练，以增加复杂性。我们遵循他们的设置，只用1000个任务来训练模型，但我们使用了预先训练好的任务标签生成器。对于一维热方程和二维高斯，我们将我们的模型性能与MAML（Finn等人（2017））进行比较，并包括我们的模型在使用和不使用任务标签生成器时的结果。

  我们计算了所有回归任务的1000个测试任务的平均平方误差，并在表1中列出了我们的结果。我们的模型在正弦波任务的两个变体上的表现都超过了Meta-SGD和BMAML。我们的模型在一维热方程和二维高斯上也取得了优异的表现。我们的结果表明，即使不使用任务标签，我们的模型设置也已经能够在这两个回归任务中表现良好。

4.1 消融研究

  此外，我们进行了一项消融研究，以研究添加任务标签生成器的效果。我们比较了我们模型的三个变体，并在高级正弦任务上对它们进行了评估。对于第一个变体，我们在训练和测试中都使用真实的任务标签。在第二个变体中，我们完全不使用任务标签。 最后，我们将这两个变体与基础模型进行比较。我们在表2中显示了这项研究的结果。

5. 结论

  我们提出了一个只关注回归任务的小样本元学习系统。我们的模型是基于基函数的线性表示的思想。我们设计了一个特征提取器网络，对整个任务分布的基函数进行编码。我们设计了一个权重生成器网络，从相同任务分布中提取的新任务的K个训练样本中生成权重。我们证明了我们的模型在各种小样本回归任务中具有竞争力。