文章目录

前言

善始者繁多，克终者盖寡。

GA（Genetic Algorithm）译为遗传算法，以达尔文进化理论为基础，模拟生物进化过程以获取问题最优解的算法。GA算法可以用来处理最值问题，在神经网络中也有广泛应用。

一、问题描述——求函数最大值

现要求函数在[0,10]内的最大值，函数为：
在这里插入图片描述
使用matplotlib绘制其图像
在这里插入图片描述

有人会说，对于这样的求最大值问题，直接穷举，挨个把x带入求出最大值不就好了吗？
对于当前问题当然是可行的，因为此时的输入较小，其范围为[0,10]，若我们要求解[0,999999]间的最大值呢？此时用穷举就太过费时费力了！！！

二、遗传算法（GA）

2.1 工作原理

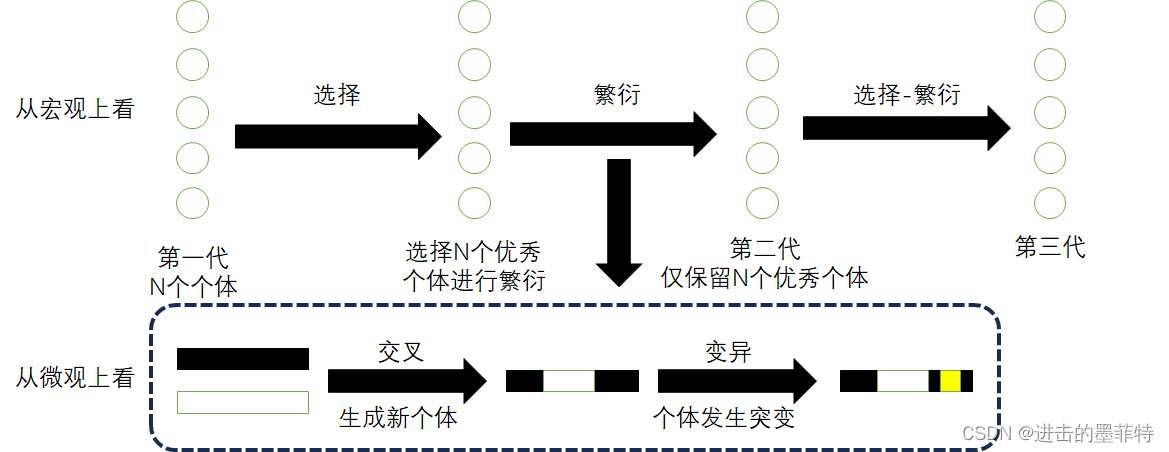
GA模拟了生物的进化过程，更为形象的例子是孟德尔的水稻杂交实验。我们用图示法来理解：
在这里插入图片描述

从宏观上看，GA是对种群进行“选择”和“繁衍”操作，在所有个体中挑选指定数量的优秀个体生成新的种群；
从微观上看，“繁衍”操作是生物DNA的改变，包含染色体的“交叉”和“变异”两个操作。

使用流程图可以表述为：
在这里插入图片描述

2.2 名词解释

生物繁衍的流程我们已经清楚，但我们还需要解决如下问题：

种群中的个体如何表示？
如果判断个体更优秀？
如何挑选更优秀的个体进行繁衍？
交叉如何实现
个体变异如何实现

2.2.1 编码——个体的表示

我们需要求第一章中函数的最大值，函数的输入是[0,10]间的有理数，可以是1,2,3这种整数，还可以是1.5,5.5这样的小数，为方便理解我们现仅考虑整数的表示（代码中是不存在此问题）。
最直接的方法时使用二进制数表示输入数据的编码。输入空间中最大值为10，所有我们使用4为二进制数就可以表示[0,10]内的所有输入：

2表示为0010；
8表示为1000；
10表示为1010.

使用二进制数表示输入的目的是：方便交叉和变异操作。通常情况下编码的长度为10或20，编码的长度越长越好，但是随着编码长度的增加，计算量也随之增大，本文中编码的长度设置为10。
但是，我们现在最大的输入才是10,10个长度的编码最大可以表示为2^10-1，即1023，例如，此时有：

2的编码表示为0000000010
3的编码表示为0000000011

这么多的空间都浪费掉了，将原问题中[0,10]作为输入不可取。

所有我们直接将10为二进制数作为输入，再经变换将其映射到区间[0,10]内，其公式为：
在这里插入图片描述
BtoD(x)表示将输入的二进制串转换为十进制数；
2^len-1表示当前二进制编码能够表示的最大值，本文中len值为10，其表示的最大值为1023；
UP表示当前输入域的最大值，本文中输入范围为[0,10]，所有此时UP值为10

例如输入1111111111，表示在函数中输入的x值为10；
例如输入0000000001，表示在函数中输入的x值为0.009775171065493646；
例如输入0000000000，表示在函数中输入的x值为0。

2.2.2 适合度——判断哪个个体更优秀

适合度描述了当前个体在当前问题的适合情况，个体的适合度越高说明该个体越优秀，那么在选择和繁衍时应当有较大概率将其保留下来。
用来计算适合度的函数就是适合度函数。 适合度函数的选择需要根据具体问题制定，本文拟求解函数的最大值，那么使用原函数即可，为保证个体的适合度不为负值，其计算公式为：
在这里插入图片描述

fitness表示个体的适合度得分；
data表示该个体在原函数上的计算值。

2.2.3 轮盘赌选择法——选择更优秀个体

“轮盘赌选择法”是一个文绉绉的叫法，简单理解：适合度更高的个体被留下的概率更高，适合度低的个体被剔除的概率更高。
在这里插入图片描述

现种群中有4个个体，分别计算出其适合度后计算每个个体适合度的比例，其中D个体的适合度比例最高，它被留下的概率最大，C被留下的概率最小，python中通过random函数实现。

个体适合度比例的计算公式为：
在这里插入图片描述

适合度比例p在后续操作中也被作为“概率”使用。

2.2.4 交叉——生成新个体

通过将两个二进制序列进行交叉，可以得到一个新的序列，我们成原来的两个二进制序列为parent，成新生成的二进制序列为child。那么问题又来了：
在哪个位置交叉呢？ 交叉位置随机选择。
交叉多少呢？ 交叉位数同样随机选择。

看个例子：
在这里插入图片描述

2.2.5 变异——增加样本输入空间

变异过程模拟了生物中的遗传与变异中的“变异”，具体操作就是改变一个二进制序列随机位置的值，将0换为1，将1换为0。变异的概率对程序的运行结果有很大的影响，通常情况下变异概率的取值范围为1%~10%。本文中变异概率取1%。

2.3 工作流程

网络中关于GA的工作流程大多描述为：
在这里插入图片描述在此基础上我们进行改进，得到如下流程图：
在这里插入图片描述

整个流程描述为：输入种群数据（二进制序列）后，将其映射到输入空间，计算个体适合度，将适合度比例转换为“概率”挑选出优秀的个体，再次计算种群中个体的适合度，因为我们有理由让优秀的个体繁衍的概率更大，最后进行交叉、变异操作生成新的种群，重复上述操作直至繁衍结束。
注意：不能够按照适合度大小来挑选适合度高的个体，假设A个体适合度10，B个体适合度10.1，我们不能够人为挑选B，因为说不定经过变异，B的适合度就高于A了，此处我们都以概率的方式决定个体的去留。

三、python代码

3.1 目标函数

def fx(x):
    return numpy.sin(10*x)*x+numpy.cos(2*x)*x
    # return x*x*x*3+x*x*2
    # return 10*numpy.sin(5*x)+7*numpy.cos(4*x)

3.2 进制转换

def otob(data):
    temp = []
    while data!=0:
        temp.append(data%2)
        data = int(data/2)
    temp.reverse()
    return temp

#DNA翻译，讲二进制转换为十进制并将其缩放到（0,10）内
def btoo(data):
    sum = 0
    for i in range(len(data)):
        sum = sum + data[i]*2**(len(data)-i-1)
    return sum/(2**DNA_SIZE-1)*10

3.3 适合度函数

为了保证程序的正常运行，在计算结果是加上一个极小值。

#定义适合度函数，此时使用原数值即可
def fitness(data):
    return data-numpy.min(data)+1e-5

3.4 选择

temp 操作表示将适合度得分转换为“概率”。此时temp为二维数组，需将其转换为一维数组。

#适者生存，从种群中挑选出指定数量的优质个体（依据适合度）
'''
    replace=True表示可以取出相同的值，默认为False
'''
def select(pop,fitness_score):
    temp = fitness_score/numpy.sum(fitness_score)
    p = []
    for data in temp:
        p.append(data[0])
    #轮渡算法，按照概率挑选个体
    index = numpy.random.choice(numpy.arange(POP_SIZE),size=POP_SIZE,replace=True,p=p)
    return pop[index]

3.5 交叉

交叉操作同样依据适合度来选择parent，因为我们有理由让适合度高的个体有更大的概率参与繁衍。

#繁衍，父母DNA配对生成新的个体（新的个体会替代原来的个体），通过交叉功能实现，交叉位置随机
def cross_fitness(pop,fitness_score):
    temp = fitness_score / numpy.sum(fitness_score)
    p = []
    for data in temp:
        p.append(data[0])
    #优秀的个体其繁衍概率应该更大
    parent1_index = numpy.random.choice(numpy.arange(POP_SIZE),p=p)
    parent2_index = numpy.random.choice(numpy.arange(POP_SIZE),p=p)
    parent1 = pop[parent1_index]
    parent2 = pop[parent2_index]
    if numpy.random.rand() <= CROSS_RATION:
        #两个体在随机位置交叉，生成新的个体，此处使用True和False数组表示
        cross_index = numpy.random.randint(0, 2, size=DNA_SIZE).astype(numpy.bool_)
        parent1[cross_index] = parent2[cross_index]
    return parent1

3.6 变异

变异操作相对简单，只需将对应位置的0和1即可。

#变异，在繁衍过程中有小概率出现变异的情况
def mutation(child):
    for i in range(DNA_SIZE):
        if numpy.random.rand() <= MUTATION_RATION:
            if child[i] == 0:
                child[i] = 1
            else:
                child[i] = 0
    return child

四、程序测试

4.1 测试程序

依据2.3中工作流程初始化种群并进行相应操作，最后使用matplotlib绘制图像。

if __name__ == '__main__':
    #生成初始种群
    pop = numpy.random.randint(0,2,size=(POP_SIZE,DNA_SIZE))
    # print(pop)
    #繁衍GENERATION次
    for i in range(GENERATION):
        #讲二进制转换为十进制
        pop_value = []
        for j in range(POP_SIZE):
            temp = []
            temp.append(btoo(pop[j]))
            pop_value.append(temp)
        # print(pop_value)
        #计算个体适合度得分，此问题中希望fx的取值尽量大，此时就通过fx的值计算适合度
        pop_value_fitness = []
        for temp_data in pop_value:
            temp = []
            temp.append(fx(temp_data[0]))
            pop_value_fitness.append(temp)
        pop_value_fitness = fitness(pop_value_fitness)
        # print(pop_value_fitness)

        #适者生存，从中群众挑选出优质的个体
        pop = select(pop,pop_value_fitness)
        # 讲二进制转换为十进制
        pop_value = []
        for j in range(POP_SIZE):
            temp = []
            temp.append(btoo(pop[j]))
            pop_value.append(temp)
        # print(pop_value)
        # 计算个体适合度得分，此问题中希望fx的取值尽量大，此时就通过fx的值计算适合度
        pop_value_fitness = []
        for temp_data in pop_value:
            temp = []
            temp.append(fx(temp_data[0]))
            pop_value_fitness.append(temp)
        pop_value_fitness = fitness(pop_value_fitness)
        #繁衍，种群中的个体进行配对
        new_pop = []
        # for parent in pop:
        #     child = cross(parent,pop)
        #     #在繁衍的过程中子代可能出现变异
        #     child = mutation(child)
        #     #将新产生的个体重新放回种群
        #     new_pop.append(child)
        for i in range(POP_SIZE):
            child = cross_fitness(pop,pop_value_fitness)
            child = mutation(child)
            new_pop.append(child)
        pop = numpy.array(new_pop)

    # 绘制原始曲线
    data = []
    xindex = []
    i = 1
    while i <= 10:
        data.append(fx(i))
        xindex.append(i)
        i += 0.1
    pyplot.plot(xindex, data)
    # 绘制经过N次繁衍后剩下种群散点分布
    # print(pop)
    data2 = []
    xindex2 = []
    for i in range(len(pop)):
        xindex2.append(btoo(pop[i]))
        data2.append(fx(btoo(pop[i])))
    print(xindex2)
    pyplot.scatter(xindex2, data2, color='red')
    pyplot.show()
    print(f"最大值为{numpy.max(data2)}")

4.2 运行结果

我们发现绝大多数点的x坐标集中在9.5附近，已经覆盖了最大值附近范围，同时图中还有一些不应当出现的点，程序还可以继续优化。
在这里插入图片描述

在这里插入图片描述

五、完整代码

import numpy
from matplotlib import pyplot

# 基因序列长度
DNA_SIZE = 10
# 初始种群数量
POP_SIZE = 100
# 交叉配对的概率
CROSS_RATION = 0.5
# 变异概率
MUTATION_RATION = 0.01
#繁衍代数
GENERATION = 500

def fx(x):
    return numpy.sin(10*x)*x+numpy.cos(2*x)*x
    # return x*x*x*3+x*x*2
    # return 10*numpy.sin(5*x)+7*numpy.cos(4*x)

def draw_primal():
    data = []
    xindex = []
    i = 1
    while i <= 10:
        data.append(fx(i))
        xindex.append(i)
        i+=0.1
    pyplot.plot(xindex,data)
    pyplot.show()

def otob(data):
    temp = []
    while data!=0:
        temp.append(data%2)
        data = int(data/2)
    temp.reverse()
    return temp

#DNA翻译，讲二进制转换为十进制并将其缩放到（0,10）内
def btoo(data):
    sum = 0
    for i in range(len(data)):
        sum = sum + data[i]*2**(len(data)-i-1)
    return sum/(2**DNA_SIZE-1)*10

#归一化处理
def guiyi(data):
    data = (data-numpy.min(data))/(numpy.max(data)-numpy.min(data))
    return data

#定义适合度函数，此时使用原数值即可
def fitness(data):
    return data-numpy.min(data)+1e-5

#适者生存，从种群中挑选出指定数量的优质个体（依据适合度）
'''
    replace=True表示可以取出相同的值，默认为False
'''
def select(pop,fitness_score):
    temp = fitness_score/numpy.sum(fitness_score)
    p = []
    for data in temp:
        p.append(data[0])
    #轮渡算法，按照概率挑选个体
    index = numpy.random.choice(numpy.arange(POP_SIZE),size=POP_SIZE,replace=True,p=p)
    return pop[index]

#繁衍，父母DNA配对生成新的个体（新的个体会替代原来的个体），通过交叉功能实现，交叉位置随机
def cross(parent,pop):
    if numpy.random.rand() <= CROSS_RATION:
        # 为parent随机寻找一个样本进行配对
        index = numpy.random.randint(0, POP_SIZE)
        # 在随机位置进行交叉
        cross_index = numpy.random.randint(0, 2, size=DNA_SIZE).astype(numpy.bool_)
        parent[cross_index] = pop[index][cross_index]
    return parent

#繁衍，父母DNA配对生成新的个体（新的个体会替代原来的个体），通过交叉功能实现，交叉位置随机
def cross_fitness(pop,fitness_score):
    temp = fitness_score / numpy.sum(fitness_score)
    p = []
    for data in temp:
        p.append(data[0])
    #优秀的个体其繁衍概率应该更大
    parent1_index = numpy.random.choice(numpy.arange(POP_SIZE),p=p)
    parent2_index = numpy.random.choice(numpy.arange(POP_SIZE),p=p)
    parent1 = pop[parent1_index]
    parent2 = pop[parent2_index]
    if numpy.random.rand() <= CROSS_RATION:
        #两个体在随机位置交叉，生成新的个体，此处使用True和False数组表示
        cross_index = numpy.random.randint(0, 2, size=DNA_SIZE).astype(numpy.bool_)
        parent1[cross_index] = parent2[cross_index]
    return parent1

#变异，在繁衍过程中有小概率出现变异的情况
def mutation(child):
    for i in range(DNA_SIZE):
        if numpy.random.rand() <= MUTATION_RATION:
            if child[i] == 0:
                child[i] = 1
            else:
                child[i] = 0
    return child

if __name__ == '__main__':
    #生成初始种群
    pop = numpy.random.randint(0,2,size=(POP_SIZE,DNA_SIZE))
    # print(pop)
    #繁衍GENERATION次
    for i in range(GENERATION):
        #讲二进制转换为十进制
        pop_value = []
        for j in range(POP_SIZE):
            temp = []
            temp.append(btoo(pop[j]))
            pop_value.append(temp)
        # print(pop_value)
        #计算个体适合度得分，此问题中希望fx的取值尽量大，此时就通过fx的值计算适合度
        pop_value_fitness = []
        for temp_data in pop_value:
            temp = []
            temp.append(fx(temp_data[0]))
            pop_value_fitness.append(temp)
        pop_value_fitness = fitness(pop_value_fitness)
        # print(pop_value_fitness)

        #适者生存，从中群众挑选出优质的个体
        pop = select(pop,pop_value_fitness)
        # 讲二进制转换为十进制
        pop_value = []
        for j in range(POP_SIZE):
            temp = []
            temp.append(btoo(pop[j]))
            pop_value.append(temp)
        # print(pop_value)
        # 计算个体适合度得分，此问题中希望fx的取值尽量大，此时就通过fx的值计算适合度
        pop_value_fitness = []
        for temp_data in pop_value:
            temp = []
            temp.append(fx(temp_data[0]))
            pop_value_fitness.append(temp)
        pop_value_fitness = fitness(pop_value_fitness)
        #繁衍，种群中的个体进行配对
        new_pop = []
        # for parent in pop:
        #     child = cross(parent,pop)
        #     #在繁衍的过程中子代可能出现变异
        #     child = mutation(child)
        #     #将新产生的个体重新放回种群
        #     new_pop.append(child)
        for i in range(POP_SIZE):
            child = cross_fitness(pop,pop_value_fitness)
            child = mutation(child)
            new_pop.append(child)
        pop = numpy.array(new_pop)

    # 绘制原始曲线
    data = []
    xindex = []
    i = 1
    while i <= 10:
        data.append(fx(i))
        xindex.append(i)
        i += 0.1
    pyplot.plot(xindex, data)
    # 绘制经过N次繁衍后剩下种群散点分布
    # print(pop)
    data2 = []
    xindex2 = []
    for i in range(len(pop)):
        xindex2.append(btoo(pop[i]))
        data2.append(fx(btoo(pop[i])))
    print(xindex2)
    pyplot.scatter(xindex2, data2, color='red')
    pyplot.show()
    print(f"最大值为{numpy.max(data2)}")
# python # 开发语言 # 算法 # 信息可视化 # matplotlib # numpy
Logo
开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

开源成为金融领域创新发展的新动力引擎

开源成为金融领域创新发展的新动力引擎

avatar 开放原子开发者工作坊

开源成为推动城市数字化转型的核心动力

城市，不仅是人们工作与生活的基本载体，更是承载着亿万人民的希望与梦想。近年来，我国智慧城市建设如火如荼，开源技术的深度融合为其发展注入了新的活力。在民生、环保、公共安全、城市服务等多个领域，开源技术的应用不仅为民众带来了切实的便捷，而且促进了政府决策的科学化，显著提升了城市综合治理能力。

avatar 开放原子开发者工作坊

OpenLoong项目通过技术监督委员会（TOC）评审

OpenLoong项目通过技术监督委员会（TOC）评审

avatar 开放原子开发者工作坊