问题定义

那么什么是不平衡数据呢？顾名思义即我们的数据集样本类别极不均衡，以二分类问题为例，假设我们的数据集是$S$，数据集中的多数类为$S_maj$，少数类为$S_min$，通常情况下把多数类样本的比例为$100:1$,$1000:1$，甚至是$10000:1$这种情况下为不平衡数据，不平衡数据的学习即需要在如此分布不均匀的数据集中学习到有用的信息。

为什么需要不平衡学习?

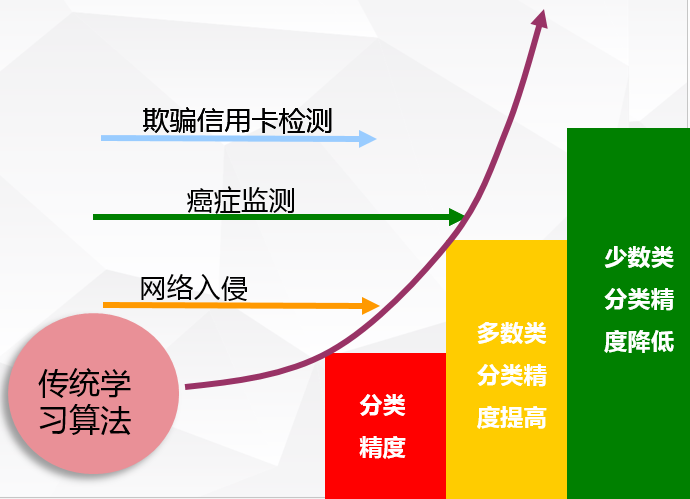
传统的学习方法以降低总体分类精度为目标，将所有样本一视同仁，同等对待，如下图1所示，造成了分类器在多数类的分类精度较高而在少数类的分类精度很低。机器学习模型都有一个待优化的损失函数，以我们最常用最简单的二元分类器逻辑回归为例，其损失函数如下公式1所示，逻辑回归以优化总体的精度为目标，不同类别的误分类情况产生的误差是相同的，考虑一个$500:1$的数据集，即使把所有样本都预测为多数类其精度也能达到$500/501$之高，很显然这并不是一个很好的学习效果，因此传统的学习算法在不平衡数据集中具有较大的局限性。

 

采样

随机采样

采样算法通过某一种策略改变样本的类别分布，以达到将不平衡分布的样本转化为相对平衡分布的样本的目的，而随机采样是采样算法中最简单也最直观易懂的一种方法。

随机采样主要分为两种类型，分别为随机欠采样（下采样）和随机过采样（上采样）两种。

随机欠采样顾名思义即从多数类$S_maj$中随机选择少量样本$E$再合并原有少数类样本作为新的训练数据集，新数据集为$S_min+E$，随机欠采样有两种类型分别为有放回和无放回两种，无放回欠采样在对多数类某样本被采样后不会再被重复采样，有放回采样则有可能。随机过采样则正好相反，即通过多次有放回随机采样从少数类$S_min$中抽取数据集$E$，采样的数量要大于原有少数类的数量，最终的训练集为$S_maj+E$。

存在的问题：

对于随机欠采样，由于采样的样本要少于原样本集合，因此会造成一些信息缺失，未被采样的样本往往带有很重要的信息，模型只学到了总体模式的一部分。

对于随机过采样，由于需要对少数类样本进行复制因此扩大了数据集，造成模型训练复杂度加大，另一方面也容易造成模型的过拟合问题。上采样后的数据集中会反复出现一些样本，训练出来的模型会有一定的过拟合；上采样会把小众样本复制多份，一个点会在高维空间中反复出现，这会导致一个问题，那就是运气好就能分对很多点，否则分错很多点。为了解决这一问题，可以在每次生成新数据点时加入轻微的随机扰动，经验表明这种做法非常有效。

Note: 值得注意的是，使用过采样方法来解决不平衡问题时应适当地应用交叉验证。这是因为过采样会观察到罕见的样本，并根据分布函数应用自举生成新的随机数据，如果在过采样之后应用交叉验证，那么我们所做的就是将我们的模型过拟合于一个特定的人工引导结果。这就是为什么在过度采样数据之前应该始终进行交叉验证，就像实现特征选择一样。只有重复采样数据可以将随机性引入到数据集中，以确保不会出现过拟合问题。

[]

针对这些问题提出了几种其它的采样算法。

过采样的改进

SMOTE算法：合成样本

SMOTE全称是Synthetic Minority Oversampling Technique即合成少数类过采样技术，它是基于随机过采样算法的一种改进方案，由于随机过采样采取简单复制样本的策略来增加少数类样本，这样容易产生模型过拟合的问题，即使得模型学习到的信息过于特别(Specific)而不够泛化(General)，SMOTE算法的基本思想是对少数类样本进行分析并根据少数类样本人工合成新样本添加到数据集中，具体如图2所示，算法流程如下。

1. 对于少数类中每一个样本$x$，以欧氏距离为标准计算它到少数类样本集$S_min$中所有样本的距离，得到其k近邻。
2. 根据样本不平衡比例设置一个采样比例以确定采样倍率$N$，对于每一个少数类样本$x$，从其k近邻中随机选择若干个样本，假设选择的近邻为$\hat{x}$。
3. 对于每一个随机选出的近邻$\hat{x}$，分别与原样本按照如下的公式构建新的样本。
   
    
   

   图2 SMOTE算法
   
   SMOTE算法摒弃了随机过采样复制样本的做法，可以防止随机过采样易过拟合的问题，实践证明此方法可以提高分类器的性能。

潜在的问题：一方面是增加了类之间重叠的可能性（由于对每个少数类样本都生成新样本，因此容易发生生成样本重叠(Overlapping)的问题），另一方面是生成一些没有提供有益信息的样本。

SMOTE改进算法，Borderline-SMOTE与ADASYN。

Borderline-SMOTE

Borderline-SMOTE的解决思路是寻找那些应该为之合成新样本的小众样本。即为每个小众样本计算K近邻，只为那些K近邻中有一半以上大众样本的小众样本生成新样本。直观地讲，只为那些周围大部分是大众样本的小众样本生成新样本，因为这些样本往往是边界样本。确定了为哪些小众样本生成新样本后再利用SMOTE生成新样本。

在Borderline-SMOTE中，若少数类样本的每个样本$x_i$求k近邻，记作$S_i-knn$，且$S_i-knn$属于整个样本集合$S$而不再是少数类样本，若满足

则将样本$x_i$加入DANGER集合，显然DANGER集合代表了接近分类边界的样本，将DANGER当作SMOTE种子样本的输入生成新样本。特别地，当上述条件取右边界，即k近邻中全部样本都是多数类时，此样本不会被选择为种样本生成新样本，此情况下的样本为噪音。

下采样的改进：Informed Undersampling

既然SMOTE可以解决随机过采样容易发生的模型过拟合问题，对应地也有一些采样方法可以解决随机欠采样造成的数据信息丢失问题，答案是Informed undersampling采样技术，informed undersampling采样技术主要有两种方法分别是EasyEnsemble算法和BalanceCascade算法。

EasyEnsemble

利用模型融合的方法（Ensemble）：多次下采样（放回采样，这样产生的训练集才相互独立）产生多个不同的训练集，进而训练多个不同的分类器，通过组合多个分类器的结果得到最终的结果。简单的最佳实践是建立n个模型，每个模型使用稀有类别的所有样本和丰富类别的n个不同样本。假设想要合并10个模型，那么将保留例如1000例稀有类别，并随机抽取10000例丰富类别。然后，只需将10000个案例分成10块，并训练10个不同的模型。

EasyEnsemble算法如下图4所示，此算法类似于随机森林的Bagging方法，它把数据划分为两部分，分别是多数类样本和少数类样本，对于多数类样本$S_maj$，通过n次有放回抽样生成n份子集，少数类样本分别和这n份样本合并训练一个模型，这样可以得到n个模型，最终的模型是这n个模型预测结果的平均值。BalanceCascade算法是一种级联算法，BalanceCascade从多数类$S_maj$中有效地选择N且满足$\midN\mid=\midS_min\mid$，将N和$\S_min$合并为新的数据集进行训练，新训练集对每个多数类样本$x_i$进行预测若预测对则$S_maj=S_maj-x_i$。依次迭代直到满足某一停止条件，最终的模型是多次迭代模型的组合。

 

BalanceCascade

利用增量训练的思想（Boosting）：先通过一次下采样产生训练集，训练一个分类器，对于那些分类正确的大众样本不放回，然后对这个更小的大众样本下采样产生训练集，训练第二个分类器，以此类推，最终组合所有分类器的结果得到最终结果。

NearMiss

利用KNN试图挑选那些最具代表性的大众样本，这类方法计算量很大。 综述“Learning from Imbalanced Data”的3.2.1节。

代价敏感学习

代价矩阵

采样算法从数据层面解决不平衡数据的学习问题，在算法层面上解决不平衡数据学习的方法主要是基于代价敏感学习算法(Cost-Sensitive Learning)，代价敏感学习方法的核心要素是代价矩阵。

我们注意到在实际的应用中不同类型的误分类情况导致的代价是不一样的，例如在医疗中，“将病人误疹为健康人”和“将健康人误疹为病人”的代价不同；在信用卡盗用检测中，“将盗用误认为正常使用”与“将正常使用识破认为盗用”的代价也不相同，因此我们定义代价矩阵如下图5所示。标记$C_ij$为将类别j误分类为类别i的代价，显然$C_00=C_11=0$，$C_01,C_10$为两种不同的误分类代价，当两者相等时为代价不敏感的学习问题。

代价敏感学习的3种方法

基于以上代价矩阵的分析，代价敏感学习方法主要有以下三种实现方式，分别是：

1. 从学习模型出发，着眼于对某一具体学习方法的改造，使之能适应不平衡数据下的学习，研究者们针对不同的学习模型如感知机，支持向量机，决策树，神经网络等分别提出了其代价敏感的版本。以代价敏感的决策树为例，可从三个方面对其进行改进以适应不平衡数据的学习，这三个方面分别是决策阈值的选择方面、分裂标准的选择方面、剪枝方面，这三个方面中都可以将代价矩阵引入，具体实现算法可参考参考文献中的相关文章。
2. 从贝叶斯风险理论出发，把代价敏感学习看成是分类结果的一种后处理，按照传统方法学习到一个模型，以实现损失最小为目标对结果进行调整，优化公式如下所示。此方法的优点在于它可以不依赖所用具体的分类器，但是缺点也很明显它要求分类器输出值为概率。
   
3. 从预处理的角度出发，将代价用于权重的调整，使得分类器满足代价敏感的特性，如基于Adaboost的权重更新策略。
4. 

魔改损失函数

[不平衡分类问题的损失函数]

[再谈类别不平衡问题：调节权重与魔改Loss的对比联系]
《从loss的硬截断、软化到focal loss》

《将“softmax+交叉熵”推广到多标签分类问题》

《通过互信息思想来缓解类别不平衡问题》

贝叶斯风险理论

再次考虑医疗诊断的问题。我们注意到,如果已给没有患癌症的病人被错误地诊断为患病,结果可能给病人带来一些压力,并且病人可能需要进一步确诊。相反,如果患癌症的病人被诊断为健康,结果可能会因为缺少治疗而使病人过早死亡。因此这两种错误的结果是相当不同的。很明显,对于第二种错误,我们最好少犯,甚至由于少犯第二种错误会导致第一种错误增加也没关系。

我们可以通过损失函数( loss function )来形式化地描述这个问题。损失函数也被称为代价函数( cost function ),是对于所有可能的决策或者动作可能产生的损失的一种整体的度量。我们的目标是最小化整体的损失。注意,有些学者不考虑损失函数,而是考虑效用函数( utility function ),并且要最大化这个函数。如果我们让效用函数等于损失函数的相反数的话,那么这些概念是等价的,因此整本书中我们都将使用损失函数这个概念。

假设对于新的 x 的值,真实的类别为 C k ,我们把 x 分类为 C j (其中 j 可能与 k 相等,也可能不相等)。这样做的结果是,我们会造成某种程度的损失,记作 Lkj ,它可以看成损失矩阵( loss matrix )的第 k, j 个元素。例如,在癌症的例子中,我们可能有图1.25所示的损失矩阵。这个特别的损失矩阵表明,如果我们做出了正确的决策,那么不会造成损失。如果健康人被诊断为患有癌症,那么损失为1。但是如果一个患有癌症的病人被诊断为健康,那么损失为1000。
最优解是使损失函数最小的解。但是,损失函数依赖于真实的类别,这是未知的（所以需要对所有的ck进行求和或者积分）。对于一个给定的输入向量 x ,我们对于真实类别的不确定性通过联合概率分布 p(x, C k ) 表示。因此,我们转而去最小化平均损失。平均损失根据这个联合概率分布计算,定义为

每一个 x 可以被独立地分到决策区域 R j 中。我们的目标是选择区域R j ,来最小化期望损失。这表明,对于每个 x ,我们要最小化 ∑k L kj p(x, C k ) 。和之前一样,我们可以使用乘积规则 p(x, C k ) = p(C k | x)p(x) 来消除共同因子 p(x) 。因此,最小化期望损失的决策规则是对于每个新的 x ,把它分到能使下式取得最小值的第 j 类:

一旦我们知道了类的后验概率 p(C k | x) 之后,这件事就很容易做了。

AdaCost算法

让我们先来简单回顾一下Adaboost算法，如下图6所示。Adaboost算法通过反复迭代，每一轮迭代学习到一个分类器，并根据当前分类器的表现更新样本的权重，如图中红框所示，其更新策略为正确分类样本权重降低，错误分类样本权重加大，最终的模型是多次迭代模型的一个加权线性组合，分类越准确的分类器将会获得越大的权重。

AdaCost算法修改了Adaboost算法的权重更新策略，其基本思想是对于代价高的误分类样本大大地提高其权重，而对于代价高的正确分类样本适当地降低其权重，使其权重降低相对较小。总体思想是代价高样本权重增加得大降低得慢。其样本权重按照如下公式进行更新。其中$\beta_+$和$\beta_-$分别表示样本被正确和错误分类情况下$\beta$的取值。

某小皮  

不平衡学习的评价方法

正确率和F值，G-Mean和ROC曲线和AUC。