
【MWORKS专业工具箱系列教程】控制系列工具箱第四期:时域分析
单位脉冲信号是一个持续时间为∆的的短脉冲,对于任意的∆值,其面积均为1,随着∆→0,𝛿Δ(𝑡)变得越来越窄,越来越高,但单位面积不变。t为标量:计算[0,t]内的响应,t为向量,计算各点的阶跃响应。t为标量:计算[0,t]内的响应,t为向量,计算各点的脉冲响应。计算任意信号响应数据,y 为响应数据数组,t 为时间向量,x 为状态数组。计算并直接返回系统阶跃响应图。计算阶跃响应数据,y 为响应数
本工具箱教程以控制系统模型创建、分析与设计流程为主线,通过大量示例介绍MWORKS控制系统工具箱的功能和具体使用。共计10篇文章,上一篇主要介绍了控制系统连接与化简。
同元软控:【MWORKS专业工具箱系列教程】控制系 列工具箱第三期:控制系统连接与化简
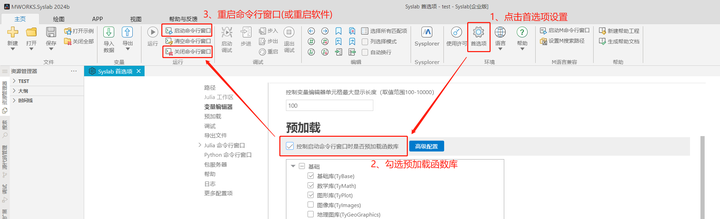
本教程代码均可直接复制到Syslab中运行,使用教程中代码前需参照下述方法加载函数库内容: 方法一:在Syslab的命令行窗口先后输入using TyControlSystems、using TyPlot和using TyBase并回车(重启软件或命令行窗口后需重新输入); 方法二:按照下图中的方法预加载函数库(设置好后每次启动软件默认加载)。
第四期:时域分析
时域分析是一种最直观、最直接的分析。一般可以为控制系统预先规定一些特殊的试验输入信号,然后比较各种系统对这些信号的响应情况。
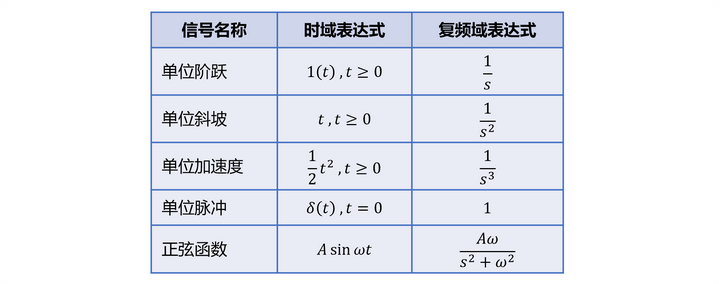
经常采用的试验输入信号
一. 阶跃响应- step()
-
对于稳定系统,通常在系统阶跃响应曲线上来定义系统动态性能指标
-
系统的单位阶跃响应不仅完整反映了系统的动态特性,而且反映了系统在单位阶跃信号输入下的稳定状态。同时,单位阶跃信号又是一个最简单、最容易实现的信号。
Syslab的 step 函数用法
| step函数调用方式 | 说明 |
|---|---|
| step(sys) | 计算并直接返回系统阶跃响应图。其中sys可以是:tf、ss、zpk |
| step(sys,t) | 计算向量 t 指定时间内的阶跃响应。t为标量:计算[0,t]内的响应,t为向量,计算各点的阶跃响应。示例: |
| step(___,fmt) | 计算并直接返回系统阶跃响应图。fmt为绘图样条属性设置字符串。示例: |
| y,t,x = step(sys, t, fig = false) | 计算阶跃响应数据,y 为响应数据数组,t 为时间向量,x 为状态数组 |
示例18:计算并绘制以下系统的阶跃响应






阶跃响应数据获取
通过下述形式可以获取到阶跃响应数据
output:
julia> t
101-element Vector{Float64}:
0.0
0.035
0.07
0.10500000000000001
0.14
0.17500000000000002
0.21000000000000002
⋮
3.325
3.3600000000000003
3.3950000000000005
3.43
3.4650000000000003
3.5000000000000004
julia> y
1×101 Matrix{Float64}:
0.0 0.0795734 0.174988 0.281454 0.394494 0.510026 … 1.00115 1.00115 1.00111 1.00105 1.00096 1.00086MIMO系统的阶跃响应
示例19:计算并绘制双输入双输出系统的阶跃响应


同样可以通过下述方式获取MIMO系统阶跃响应数据
 output:
output:
julia> t
1301-element Vector{Float64}:
0.0
0.09210340371972092
0.18420680743944184
0.27631021115916277
0.3684136148788837
0.4605170185986046
0.5526204223183255
⋮
119.27390781703859
119.36601122075831
119.45811462447804
119.55021802819776
119.64232143191748
119.7344248356372
julia> y
2×1301×2 Array{Float64, 3}:
[:, :, 1] =
0.0 0.0830874 0.14644 0.188473 0.208858 0.208431 … -0.153846 -0.153846 -0.153846 -0.153846 -0.153846
0.0 0.117899 0.279744 0.473182 0.685291 0.903305 1.15385 1.15385 1.15385 1.15385 1.15385
[:, :, 2] =
0.0 0.0871829 0.162123 0.221969 0.264909 0.290181 … -6.93889e-17 -6.93889e-17 -6.93889e-17 -6.93889e-17
0.0 0.0266207 0.101938 0.217719 0.364331 0.531374 1.0 1.0 1.0 1.0对于MIMO系统的响应数据 y 为一个三维数组,其维度为:![]() ,其中:
,其中:
-
为系统输出数量
-
为时间向量长度
-
为系统输入数量
因此,通过 y[i,:,j] 可取出第 i 个输入到第 j 个输出的阶跃响应数据向量。
小彩蛋:二阶系统响应面绘制
示例20:计算并绘制标准二阶系统阶跃响应曲线及响应面
① 阶跃响应曲线计算与绘制


② 阶跃响应面绘制


时域性能指标获取
通常控制系统的性能指标以系统对单位阶跃输入量的瞬态响应形式给出。
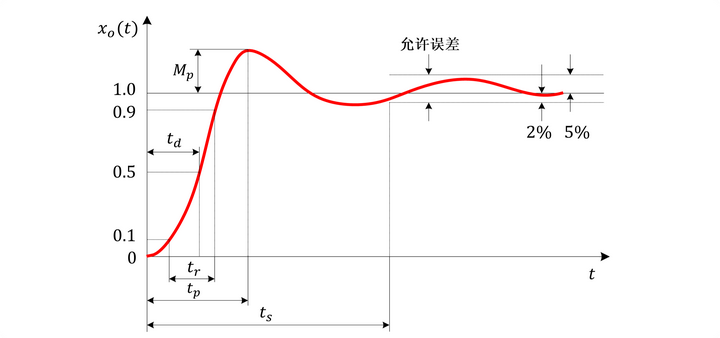

通过 stepinfo() 函数计算并获取动态系统阶跃响应特性
示例21:获取系统的阶跃响应特性


output:
julia> # 上升时间
julia> res.RiseTime
1×1 Matrix{Float64}:
0.2647250314828522
julia> # 最大超调
julia> res.Overshoot
1×1 Matrix{Float64}:
37.1410271661408
julia> # 峰值
julia> res.Peak
1×1 Matrix{Float64}:
1.371410271661408
julia> # 峰值时间
julia> res.PeakTime
1×1 Matrix{Float64}:
0.6447238260382373
julia> # 调整时间
julia> res.SettlingTime
1×1 Matrix{Float64}:
2.246034069329275二、脉冲响应- impulse()
系统的脉冲响应(或称为冲激响应)可以用 impulse() 函数进行计算并绘制脉冲响应图。
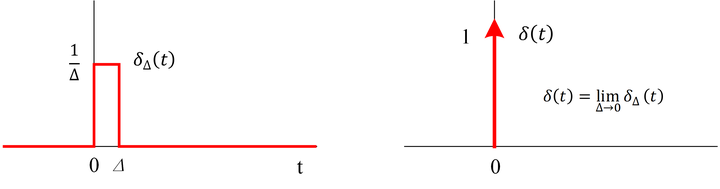
连续时间单位脉冲信号是一个持续时间为∆的的短脉冲,对于任意的∆值,其面积均为1,随着∆→0,𝛿Δ(𝑡)变得越来越窄,越来越高,但单位面积不变。

Syslab的 impulse 函数用法
| impulse 调用方式 | 说明 |
|---|---|
| impulse(sys) | 计算并直接返回系统脉冲响应图。其中sys可以是:tf、ss、zpk |
| impulse(sys,t) | 计算向量 t 指定时间内的脉冲响应。t为标量:计算[0,t]内的响应,t为向量,计算各点的脉冲响应。示例: |
| impulse(___,fmt) | 计算并直接返回系统脉冲响应图。fmt为绘图样条属性设置字符串。示例: |
| y,t,x = impulse (sys, t, fig = false) | 计算阶跃响应数据,y 为响应数据数组,t 为时间向量,x 为状态数组 |
示例22:计算以下系统的脉冲响应

output:


output:
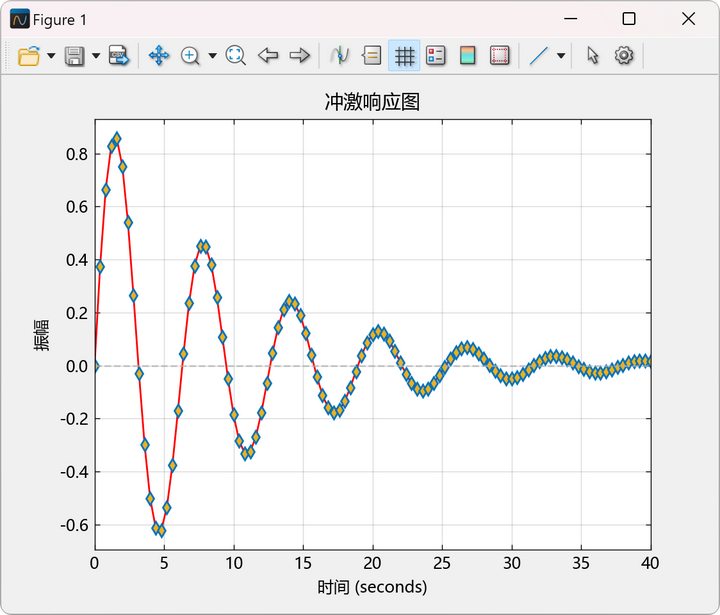
同样的,可以通过下述形式获取脉冲响应数据:

output:
julia> t
1906-element Vector{Float64}:
0.0
0.3141592653589793
0.6283185307179586
0.9424777960769379
1.2566370614359172
1.5707963267948966
1.8849555921538759
⋮
596.9026041820607
597.2167634474197
597.5309227127786
597.8450819781376
598.1592412434966
598.4734005088555
julia> y
1×1906 Matrix{Float64}:
0.0 0.299509 0.552363 0.737413 0.841231 0.858915 … -7.88052e-27 -9.66575e-27 -1.04252e-26 -1.01493e-26小技巧:求脉冲响应的另一种方法
考虑系统的脉冲响应表达式为:
,其中脉冲信号

因此,求取
的脉冲响应,可以转化为求取
的单位阶跃响应
示例23:针对示例22,通过阶跃函数求取其脉冲响应


三. 斜坡信号响应
Syslab控制工具箱没有提供斜坡信号响应函数,同样可以考虑使用上一节中等效的方法进行求取。
考虑系统的斜坡响应表达式为:
,其中斜坡信号:

的斜坡响应,转化为求取
的单位阶跃响应
示例24:计算以下系统的斜坡响应


output:
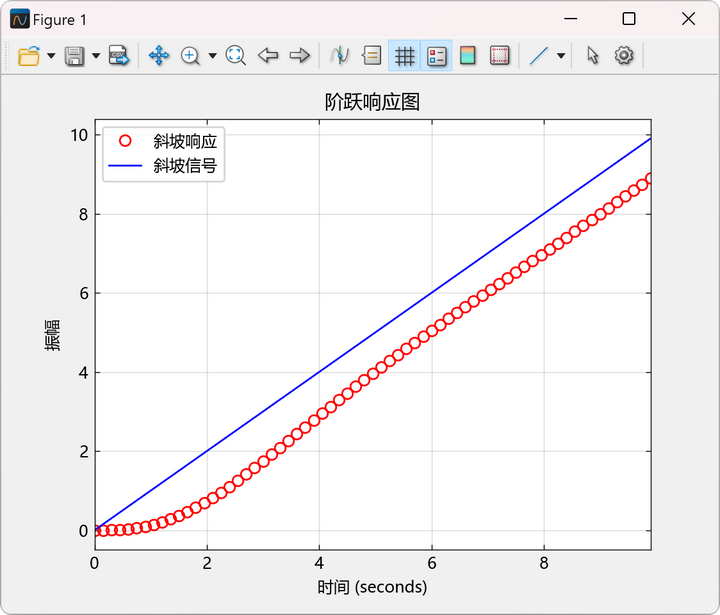
类似的,系统对单位加速度信号的响应可以使用同样的方式计算得到。
四. 对任意信号的响应- lsim()
为了求对任意输入信号的响应,可以使用 lsim() 函数
Syslab的 lsim 函数使用
| lsim调用方式 | 说明 |
|---|---|
| lsim(sys,u,t) | 计算并直接返回系统对输入信号(t,u)的时域响应图。其中 t 为时间向量 |
| lsim(sys,u,t,fmt) | 计算并直接返回系统对输入信号(t,u)的时域响应图。fmt为绘图样条属性设置字符串。示例: |
| lsim(sys,u,t,x0 = value) | 当sys是状态空间模型时,可以进一步指定初始状态值 x0 ,注意 x0 为向量形式 |
| lsim(sys,u,t,x0 = value,fmt) | 当sys是状态空间模型时,可以进一步指定初始状态值 x0 ,fmt为绘图样条属性设置字符串 |
| res = lsim (sys, u, t, fig = false) | 计算任意信号响应数据,生成 res 响应数据为SimResult结构体,不出图。其中: |
| y,t,x = lsim (sys, u, t, fig = false) | 计算任意信号响应数据,y 为响应数据数组,t 为时间向量,x 为状态数组 |

output:
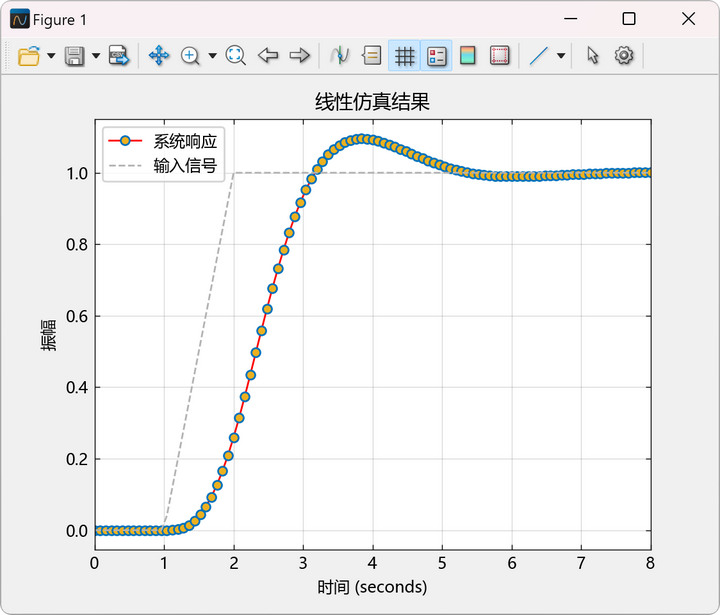
示例26:考虑以下系统在输入信号 作用下的响应情况,假设初始状态为


output:
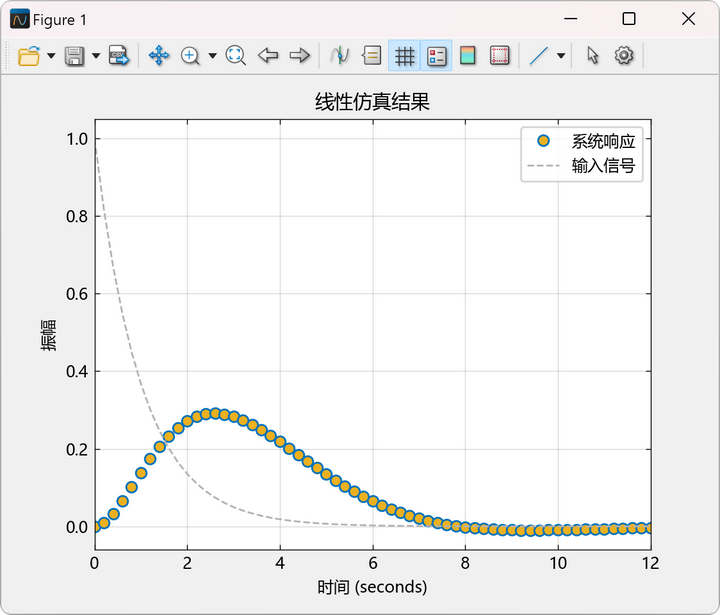
改变初始状态为:![]()

output:
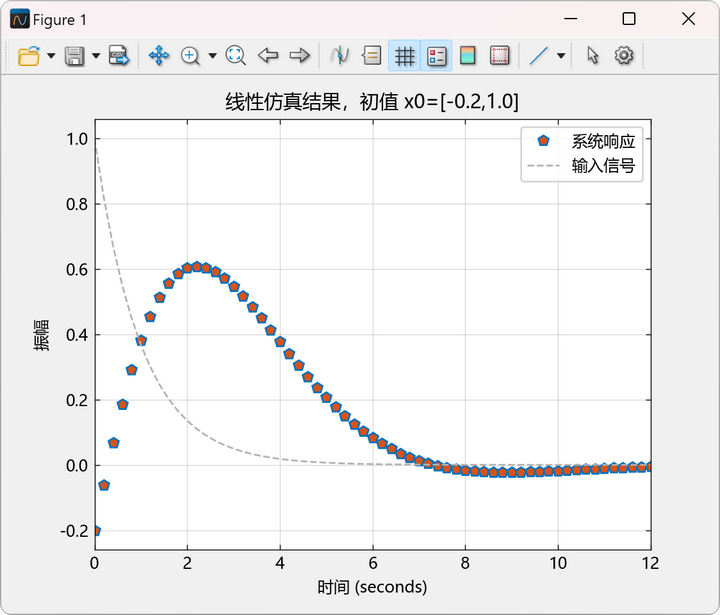
其余函数请参阅Syslab-控制系统工具箱帮助文档
"Syslab控制系统工具箱-时域分析"帮助文档![]() https://www.tongyuan.cc/help/SyslabHelp.html#/Doc/TyControlSystems/LinearAnalysis/TimeAndFrequencyDomainAnalysis.html%23%E6%97%B6%E5%9F%9F%E5%88%86%E6%9E%90本系列第五期文章将对频域分析进行详尽解读,敬请关注!
https://www.tongyuan.cc/help/SyslabHelp.html#/Doc/TyControlSystems/LinearAnalysis/TimeAndFrequencyDomainAnalysis.html%23%E6%97%B6%E5%9F%9F%E5%88%86%E6%9E%90本系列第五期文章将对频域分析进行详尽解读,敬请关注!

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献15条内容
已为社区贡献15条内容





所有评论(0)