目录

1.FAST-ICA算法理论概述

2.FAST-ICA算法MATLAB核心程序

3.MATLAB仿真结果

---

1.FAST-ICA算法理论概述

       混合信号分离是一种广泛使用的技术，可以应用于各种领域，例如语音信号处理，医学信号处理和通信系统等。在混合信号中，多个信号混合在一起，无法直接进行识别或处理。因此，需要采用一些技术手段将混合信号中的各个成分分离出来，以便进行后续的分析和处理。

      ICA算法是一种常用的混合信号分离方法。其基本原理是将混合信号通过线性变换分解为相互独立的成分，每个成分具有尽可能大的方差。ICA算法的流程包括以下步骤：

      归一化：将混合信号进行归一化处理，使其具有零均值和单位方差。这样可以简化ICA算法的计算过程。

      白化：在归一化之后，对混合信号进行白化处理，使其各成分不相关并且具有单位方差。白化处理可以使用以下公式进行：

x'=ED-1/2ETx

其中D-1/2=diag(d1-1/2，…，dn-1/2)，E{x'x'T}=I。通过白化处理，混合信号的各成分之间将具有单位方差并且不相关。
       FastICA算法：FastICA算法，又称不动点(Fixed-Point)算法，是由芬兰赫尔辛基大学Hyvärinen等人提出来的。是一种快速寻优迭代算法，与普通的神经网络算法不同的是这种算法采用了批处理的方式，即在每一步迭代中有大量的样本数据参与运算。但是从分布式并行处理的观点看该算法仍可称之为是一种神经网络算法。
       FastICA算法有基于峭度、基于似然最大、基于负熵最大等形式，这里，我们介绍基于负熵最大的FastICA算法（可以有效地把不动点迭代所带来的优良算法特性与负熵所带来的更好统计特性结合起来）。它以负熵最大作为一个搜寻方向，可以实现顺序地提取独立源，充分体现了投影追踪（Projection Pursuit）这种传统线性变换的思想。此外，该算法采用了定点迭代的优化算法，使得收敛更加快速、稳健。
       因为FastICA算法以负熵最大作为一个搜寻方向，因此先讨论一下负熵判决准则。由信息论理论可知：在所有等方差的随机变量中，高斯变量的熵最大，因而我们可以利用熵来度量非高斯性，常用熵的修正形式，即负熵。根据中心极限定理，若一随机变量由许多相互独立的随机变量之和组成，只要具有有限的均值和方差，则不论其为何种分布，随机变量较更接近高斯分布。换言之，较的非高斯性更强。因此，在分离过程中，可通过对分离结果的非高斯性度量来表示分离结果间的相互独立性，当非高斯性度量达到最大时，则表明已完成对各独立分量的分离。

       在实际应用中，需要一种最大化目标函数的算法来分离混合信号。FastICA算法是一种常用的ICA算法，其目标函数通常表示为非高斯性测量的负值，通过迭代更新混合信号的估计值，使得目标函数达到最大值，从而将混合信号分离为相互独立的成分。

FastICA算法的迭代步骤如下：

       设x是混合信号，s是估计的分离信号，A是混合矩阵，A'是白化混合矩阵。首先将观测数据进行白化处理：x'=ED-1/2ETx。然后根据以下步骤进行迭代：

(1) 对白化后的信号x'进行固定点运算，得到估计的分离信号s'；
(2) 对s'进行逆白化处理：s=D1/2ETs'；
(3) 计算分离信号s的均值A'm=E{s}；
(4) 计算归一化向量s=s-A'm；
(5) 计算白化矩阵D-1/2=diag(d1-1/2，…，dn-1/2)，其中d1，…，dn是s的前n个奇异值；
(6) 计算白化后的向量x'=ED-1/2ETx；
(7) 计算混合矩阵A'=E{x'x'T}；
(8) 计算FastICA算法的权值向量w=E{s'x'}；
(9) 计算新的分离信号s''=w x'；
(10) 对s''进行逆白化处理：s=D-1/2ETs''；
(11) 计算新的分离信号的均值A'm=E{s}；
(12) 计算新的归一化向量s=s-A'm；
(13) 如果达到预设的迭代次数或者目标函数收敛，则停止迭代；否则返回步骤(1)。

      通过以上迭代步骤，FastICA算法可以将混合信号分离为相互独立的成分。在分离过程中，先对观测信号进行白化处理，使得各成分不相关并且具有单位方差。然后使用FastICA算法进行迭代更新，将观测信号分离为相互独立的成分。

2.FAST-ICA算法MATLAB核心程序

% 【功能】使用FastICA算法计算独立成分分析  
% 【输入】Z - 输入数据（矩阵），r - 所需的独立成分数量，type - 类型（kurtosis或negentropy），flag - 标记（未使用）  
% 【输出】Zica - 独立成分（矩阵），W - 转换矩阵，T - 转换矩阵，mu - 未使用（固定为1） 
function [Zica, W, T, mu] = fastICA(Z,r,type,flag)
% 收敛标准（默认值为1e-6）  
TOL = 1e-6;         % Convergence criteria
MAX_ITERS = 100;    % 最大迭代次数（默认值为100） 
% 检查type参数是否存在或是否为空，若否，设定为默认值'kurtosis'  
if ~exist('type','var') || isempty(type)
    % Default type
    type = 'kurtosis';
end
n = size(Z,2);% 获取输入数据Z的列数（即样本数）  

% 根据type参数设定算法类型  
% Kurtosis（峰度）算法  
% Negentropy（负熵）算法  
% Set type  
if strncmpi(type,'kurtosis',1)
    % Kurtosis
    USE_KURTOSIS = true;
    algoStr = 'kurtosis';
elseif strncmpi(type,'negentropy',1)
    % Negentropy
    USE_KURTOSIS = false;
    algoStr = 'negentropy';
end
% 对输入数据进行中心化（每一列减去其均值） 
[Zc, mu] = centerRows(Z);
% 对中心化后的数据进行白化（去相关性）  
[Zcw, T] = whitenRows(Zc);
% 定义一个函数用于计算每一行的L2范数（白化后数据的方差）并返回标准化后的结果  
normRows = @(X) bsxfun(@rdivide,X,sqrt(sum(X.^2,2)));
% 随机初始化权重矩阵W，大小为r x size(Z,1)  
W = normRows(rand(r,size(Z,1))); % Random initial weights
k = 0;
delta = inf;
while delta > TOL && k < MAX_ITERS
    k = k + 1;
    
    Wlast = W;  % 保存上次迭代的权重矩阵W  
    Sk = W * Zcw;% 将权重矩阵W与白化后的数据Zcw相乘，得到Sk 
    if USE_KURTOSIS
        %  % Kurtosis方法对应的G和Gp计算方式  
        G = 4 * Sk.^3;
        Gp = 12 * Sk.^2;
    else
        % Negentropy方法对应的G和Gp计算方式  
        G = Sk .* exp(-0.5 * Sk.^2);
        Gp = (1 - Sk.^2) .* exp(-0.5 * Sk.^2);
    end
    % 根据G和Gp更新权重矩阵W
    W = (G * Zcw') / n - bsxfun(@times,mean(Gp,2),W);
    W = normRows(W); % 对权重矩阵W进行L2范数标准化  
    
    % 解耦权重矩阵W，使其成为正交矩阵U和特征值矩阵S的乘积，U的列向量是单位向量组，S是对角矩阵，对角线元素是特征值（按降序排列）  
    [U, S, ~] = svd(W,'econ');
    % 将权重矩阵W转化为正交基U和特征值S的乘积，并对W进行归一化处理，保证其列向量的L2范数为一单位向量，且对应于最大特征值的特征向量为全1向量/单位向量  times  其对角线元素S的特征值的逆的对角线元素  times  正交基U的转置  times  权重矩阵W，这里实现了对权重矩阵W的归一化处理，使得每个特征值对应的特征向量的L2范数为1，并且保证了最大的特征值对应的特征向量为全1向量/单位向量  times  其对角线元素S的特征值的逆的对角线元素  times  正交基U
    W = U * diag(1 ./ diag(S)) * U' * W;
 
    delta = max(1 - abs(dot(W,Wlast,2)));

end
 
Zica = W * Zcw;
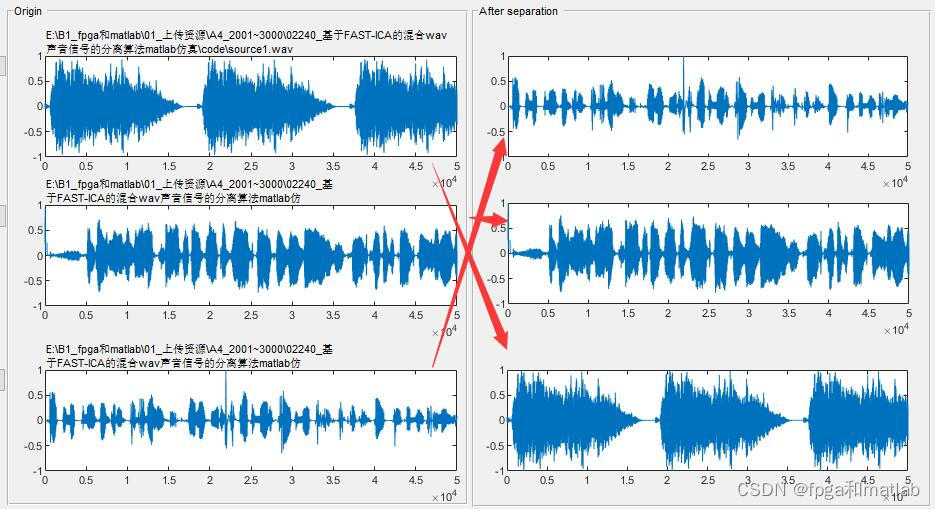
up2240

3.MATLAB仿真结果

      由于FAST-ICA是一种基于非高斯性的独立成分分析方法，它可能无法完全准确地恢复出所有的源信号。特别是当源信号具有相似的特性时，恢复可能会变得非常困难。因此，使用ICA时应当谨慎，并可能需要尝试不同的参数设置。