正负样本分配策略(OTA, SimOTA,TAS)
SimOTA可以理解为是一种匹配策略的方法,可以看成是一个最优传输的问题。举一个通俗易懂的例 子就是,有2个分配基地与6个周围城市,现在需要考虑一个最优的配送方式来确保分配东西到这几个 城市的运输成本是最低的。而对于目标检测来说,这个最优传输问题也就是一个最优分配问题,如何 实现把这些anchor point分配给gt的代价 (cost) 是最低的。这个代价就是iou损失,分类损失等内容。
OTA
论文:《OTA: Optimal Transport Assignment for Object Detection》
代码:Megvii-BaseDetection/OTA
标签分配算法
目标CNN-based的目标检测器是预测 pre-defined anchors 的类别 (cls) 以及偏移量 (reg) 。
为了训练目标检测器,需要为每个anchor 分配 cls 和 reg 目标,这个过程称为标签分配或者正采样。
一些经典的标签分配方法:
- RetinaNet、Faster-RCNN: 使用 pre-defined anchors 与 groudtruth 的 IoU 阈值来区分正负样本。
- YOLOV5: 为了增加正样本数量,使用 pre-defined anchors 与 groudtruth 的 宽高比进行正采样。
- FCOS:处于groundtruth的中心区域的anchors作为正样本。
OTA的提出背景
使用人工规则的分配方法,无法考虑尺寸、形状或边界遮挡的差异性。
虽然有一些改进工作,如ATSS动态分配方法,可以为每个目标动态的选择正样本。
但是上述方法都一个缺陷:没有全局性的考虑,比如当处理模糊标签时 (一个anchor可能对应多个目标),对其分配任何一个标签都可能对网络学习产生负面影响。
OTA就是解决上述问题,以获得全局最优的分配策略。
OTA思想
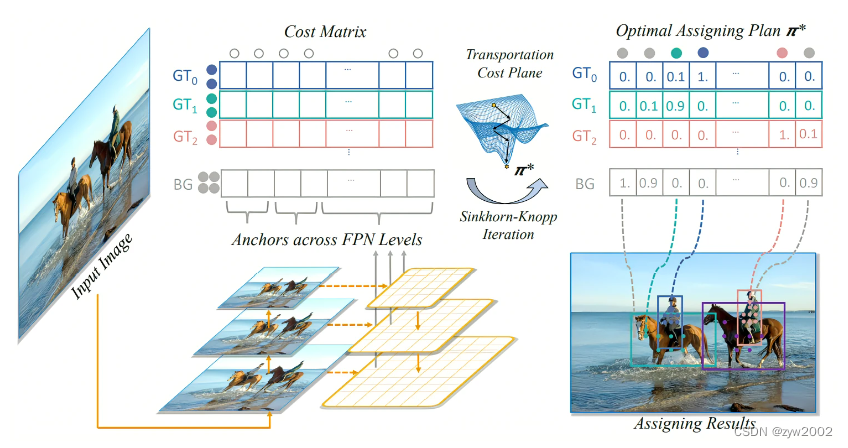
为了得到全局最优的分配策略,OTA方法提出将标签分配问题当作 Optimal Transport (OT) 问题。
具体来讲:
将每个gt当作可以提供一定数量labels的supplier,而每个anchor可以看作是需要唯一label 的 demander,如果某个anchor从 gt 那儿获得足够的 label,那么这个 anchor 就是此 gt 的一个正样本。
因为有很多anchor是负样本,所以还需引入另一个background供应商,专门为anchor提供 negative 标签,
问题目标是 supplier如何分配 label 给demander,可以让 cost 最低。其中 cost 的定义为:
对于每个anchor-gt pair,cost 为 pair-wise cls loss 和 pair-wise reg loss的加权和。
对于每个anchor-background pair,cost 为 pair-wise cls loss这一项。

Optimal Transport的求解过程
假设第
i
\mathrm{i}
i 个 supplier 拥有
s
i
\mathrm{s}_{\mathrm{i}}
si 个货物,第
j
\mathrm{j}
j 个 demander 需要
d
j
\mathrm{d}_{\mathrm{j}}
dj 个货物。
货物从 supplier i运到demander
j
\mathrm{j}
j 的成本为
c
i
j
\mathrm{c}_{\mathrm{ij}}
cij 。
目标是找到最佳运输方案
π
∗
=
π
i
,
j
∣
i
=
1
,
2
,
…
,
m
,
j
=
1
,
2
,
…
n
\pi^*=\pi_{\mathrm{i}, \mathrm{j}} \mid \mathrm{i}=1,2, \ldots, \mathrm{m}, \mathrm{j}=1,2, \ldots \mathrm{n}
π∗=πi,j∣i=1,2,…,m,j=1,2,…n ,可以让总的运输 cost 最低:
min
π
∑
i
=
1
m
∑
j
=
1
n
c
i
j
π
i
j
s.t.
∑
i
=
1
m
π
i
j
=
d
j
,
∑
j
=
1
n
π
i
j
=
s
i
,
∑
i
=
1
m
s
i
=
∑
j
=
1
n
d
j
π
i
j
≥
0
,
i
=
1
,
2
,
…
,
m
,
j
=
1
,
2
,
…
,
n
\begin{gathered} \min _\pi \sum_{\mathrm{i}=1}^{\mathrm{m}} \sum_{\mathrm{j}=1}^{\mathrm{n}} \mathrm{c}_{\mathrm{ij}} \pi_{\mathrm{ij}} \\ \text { s.t. } \sum_{\mathrm{i}=1}^{\mathrm{m}} \pi_{\mathrm{ij}}=\mathrm{d}_{\mathrm{j}}, \sum_{\mathrm{j}=1}^{\mathrm{n}} \pi_{\mathrm{ij}}=\mathrm{s}_{\mathrm{i}}, \sum_{\mathrm{i}=1}^{\mathrm{m}} \mathrm{s}_{\mathrm{i}}=\sum_{\mathrm{j}=1}^{\mathrm{n}} \mathrm{d}_{\mathrm{j}} \\ \pi_{\mathrm{ij}} \geq 0, \mathrm{i}=1,2, \ldots, \mathrm{m}, \mathrm{j}=1,2, \ldots, \mathrm{n} \end{gathered}
πmini=1∑mj=1∑ncijπij s.t. i=1∑mπij=dj,j=1∑nπij=si,i=1∑msi=j=1∑ndjπij≥0,i=1,2,…,m,j=1,2,…,n
上述问题可以使用 Sinkhorn-Knopp 算法来求解。
OT for Label Assignment
回到标签分配问题,对于一张图片,假设有
m
\mathrm{m}
m 个
g
t
\mathrm{gt}
gt 目标和
n
\mathrm{n}
n 个 anchors:
- 毎个gt 拥有 k \mathrm{k} k 个positive labels,即 s i = k ; i = 1 , 2 , . . , m \mathrm{s}_{\mathrm{i}}=\mathrm{k} ; \mathrm{i}=1,2, . ., \mathrm{m} si=k;i=1,2,..,m ;
- 毎个anchor 需要一个 label, 即
d
j
=
1
;
j
=
1
,
2
,
…
,
n
\mathrm{d}_{\mathrm{j}}=1 ; \mathrm{j}=1,2, \ldots, \mathrm{n}
dj=1;j=1,2,…,n
将一个 positive label 从 g t i \mathrm{gt}_{\mathrm{i}} gti 运到 anchor a i \mathrm{a}_{\mathrm{i}} ai 的成本为 c i j f g \mathrm{c}_{\mathrm{ij}}^{\mathrm{fg}} cijfg, 其可以表示为:
c i j f g = L c l s ( P j c l s ( θ ) , G i c l s ) + α L r e g ( P j b o x ( θ ) , G i b o x ) c_{\mathrm{ij}}^{\mathrm{fg}}=\mathrm{L}_{\mathrm{cls}}\left(\mathrm{P}_{\mathrm{j}}^{\mathrm{cls}}(\theta), \mathrm{G}_{\mathrm{i}}^{\mathrm{cls}}\right)+\alpha \mathrm{L}_{\mathrm{reg}}\left(\mathrm{P}_{\mathrm{j}}^{\mathrm{box}}(\theta), \mathrm{G}_{\mathrm{i}}^{\mathrm{box}}\right) cijfg=Lcls(Pjcls(θ),Gicls)+αLreg(Pjbox(θ),Gibox)
式中:
P j c l s \mathrm{P}_{\mathrm{j}}^{\mathrm{cls}} Pjcls 和 P j box \mathrm{P}_{\mathrm{j}}^{\text {box }} Pjbox 分别表示对 anchor a j \mathrm{a}_{\mathrm{j}} aj 预测的 cls score 和 bbox;
G i c l s \mathrm{G}_{\mathrm{i}}^{\mathrm{cls}} Gicls 和 G i b o x \mathrm{G}_{\mathrm{i}}^{\mathrm{box}} Gibox 分别表示对 g t j \mathrm{gt} \mathrm{j} gtj 的 cls 和 bbox;
L c l s \mathrm{L}_{\mathrm{cls}} Lcls 和 L b o x \mathrm{L}_{\mathrm{box}} Lbox 分别表示 cross entorpy loss 和 IoU Loss;
α \alpha α 是 2 个loss的平衡系数
此外很多anchor是负样本,所以还有一个background supplier,将一个negative label 从background supplier 运到 anchor a j a_j aj 的成本为 c j b g c_j^{\mathrm{bg}} cjbg ,其可以表示为:
c j b g = L c l s ( P j c l s ( θ ) , ϕ ) \mathrm{c}_{\mathrm{j}}^{\mathrm{bg}}=\mathrm{L}_{\mathrm{cls}}\left(\mathrm{P}_{\mathrm{j}}^{\mathrm{cls}}(\theta), \phi\right) cjbg=Lcls(Pjcls(θ),ϕ)
可以计算出negative lables的总数为: n − m × k \mathrm{n}-\mathrm{m} \times \mathrm{k} n−m×k ,所以 s i \mathrm{s}_{\mathrm{i}} si 更新为:
s i = { k i ≤ m n − m × k otherwise \mathrm{s}_{\mathrm{i}}= \begin{cases}\mathrm{k} & \mathrm{i} \leq \mathrm{m} \\ \mathrm{n}-\mathrm{m} \times \mathrm{k} & \text { otherwise }\end{cases} si={kn−m×ki≤m otherwise
SimOTA
SimOTA的简要介绍
SimOTA可以理解为是一种匹配策略的方法,可以看成是一个最优传输的问题。举一个通俗易懂的例 子就是,有2个分配基地与6个周围城市,现在需要考虑一个最优的配送方式来确保分配东西到这几个 城市的运输成本是最低的。而对于目标检测来说,这个最优传输问题也就是一个最优分配问题,如何 实现把这些anchor point分配给gt的代价 (cost) 是最低的。这个代价就是iou损失,分类损失等内容。
在论文中, cost的公式为:
c
i
j
=
L
i
j
c
l
s
+
λ
L
i
j
r
e
g
\mathrm{c}_{\mathrm{ij}}=\mathrm{L}_{\mathrm{ij}}^{\mathrm{cls}}+\lambda \mathrm{L}_{\mathrm{ij}}^{\mathrm{reg}}
cij=Lijcls+λLijreg
也就是说,对于一张特征图上的所有anchor point来说,整个匹配的策略代价是所有特征点与每一个gt box所产生的分类损失与回归损失之和。但是实际代码中的cost计算公式是稍微不一样的:
cost = (
pair_wise_cls_loss
+ 3.0 * pair_wise_ious_loss
+ 100000.0 * (~is_in_boxes_and_center)
)
pair_wise_cls_loss就是每个样本与每个GT之间的分类损失 L i j c l s L_{ij}^{cls} Lijclspair_wise_ious_loss是每个样本与每个GT之间的回归损失 L i j r e g \mathrm{L}_{\mathrm{ij}}^{\mathrm{reg}} Lijregis_in_boxes_and_center代表那些落入GT Bbox与fixed center area交集内的样本,即上图中橙色 勾对应的样本,然后这里进行了取反 表示不在GT Bbox与fixed center area交集内的样本 (非 橙色样本),即上图中黑色勾对应的样本。接着又乘以100000.0,也就是说对于GT Bbox与fixed center area交集外的样本cost加上了一个非常大的数,这样在最小化cost过程中会优先选择GT Bbox与fixed center area交集内的样本。
SimOTA的流程
SimOTA具体的做法是首先计算每个目标Cost最低的10特征点,然后把这十个特征点对应的预测框与真实框的IOU加起来求得最终的k。这一部分就是对框进行筛选。
首先进行初步的框筛选:
- 根据中心点判断:寻找anchor box中心点,落在gt_box矩形范围内的anchors
- 根据目标框来预测:以gt中心点为基准,设置边长为5的正方形,挑选正方形内所有的锚框。
经过初步筛选后则可以精细化筛选:
- 初筛正样本信息提取
- Loss函数计算
- cost成本计算
- SimOTA求解
SimOTA的详细实现流程
-
首先需要对anchor point进行一个预筛选。在SimOTA中,首先会对gt boxs位置范围内的所有anchor point进行框选,其次在gt boxs位置范围内设定一个5x5大小的box,称之为fixed center area,如下图所示。这些被gt box与fixed center area框选出来的anchor point就是预筛选的目标。

-
针对这些设计多个gt box所获取的anchor point,现在假设有3个gt box的范围中涵盖了1000个anchor point。那么,现在需要做的就是分别对每一个anchor point计算其相对与每一个gt box的分类损失cls_loss、位置损失iou_loss。从而根据分类损失cls_loss、位置损失iou_loss获取cost矩阵以及iou矩阵

-
现在就可以根据所获得的iou矩阵来选择出n_candidate_k个iou最大的候选框,topk_ious(n_candidate_k是取10和Anchor Point数量之间的最小值)。需要需要注意,这里的iou矩阵只是为了确定dynamic_k,也就是动态的选择为每一个gt box赋予多少个正样本。

当获取到每个gt box最高的前k个iou数值时,这里会对他们进行一个求和处理。这里获取出来的值是处于[0, n_candidate_k]之间的。如果是浮点数值,则对其进行向下取整处理。所获取的最后数值dynamic_k,就是每个针对每个gt box分配的anchor point数。
其中对iou矩阵进行topk,可以获取与每一个gt box的iou最大的前k的iou值与索引的,只是这里只需要返回最大的数值而不需要要返回索引。 -
现在对每个gt box进行动态的缺点分配的anchor point数之后,就根据cost矩阵来确定。这里会对每一个gt box来分配cost值最低的dynamic_k个anchor point。对于代码中的公式也可以知道,只有位于当前gt box的fixed center area内区域的anchor point所对应的cost才会比较低,其余的gt box内的剩余地方因为分配的权重过大,所以cost必定很大,而不再gt box的cost就更大了。
 根据cost值的挑选出来的几个最低anchor point,可以再构建一个Anchor Point分配矩阵,记录每个GT对应哪些正样本,对应正样本的位置标1,其他位置标0。如上图所示。
根据cost值的挑选出来的几个最低anchor point,可以再构建一个Anchor Point分配矩阵,记录每个GT对应哪些正样本,对应正样本的位置标1,其他位置标0。如上图所示。 -
对于重复预测框对应不同的gt目标框,即第五列所对应的候选框,被目标检测框1和2,都进行关联。对这两个位置,还要使用cost值进行对比,选择较小的值,再进一步筛选。确保一个gt只分配给一个anchor point。
-
根据以上流程就能找到所有的正样本以及正样本对应的GT了,那么剩下的Anchor Point全部归为负样本。对筛选预测框进行loss计算,要注意的是这里的iou_loss和cls_loss,只针对目标框和筛选出的正样本预测框进行计算,而obj_loss还是针对所有的anchor point(包含所有的正样本与负样本)
Loss = 1 N p o s ( L c l s + λ L r e g + L o b j ) \text { Loss }=\frac{1}{\mathrm{~N}_{\mathrm{pos}}}\left(\mathrm{L}_{\mathrm{cls}}+\lambda \mathrm{L}_{\mathrm{reg}}+\mathrm{L}_{\mathrm{obj}}\right) Loss = Npos1(Lcls+λLreg+Lobj)
其中: L c l s \mathrm{L}_{\mathrm{cls}} Lcls 代表分类损失; L r e g \mathrm{L}_{\mathrm{reg}} Lreg 代表定位损失; L o b j \mathrm{L}_{\mathrm{obj}} Lobj 代表obb损失; λ \lambda λ 代表定位损失的平衡系数, 源码中设置是5.0; N p o s \mathrm{N}_{\mathrm{pos}} Npos 代表被分为正样的Anchor Point数。
TAL
论文: 《TOOD: Task-aligned One-stage Object Detection》
代码:fcjian/TOOD
TAL(Task Aligned Learning)的提出背景
物体检测方法的2个局限性:
①分类和定位的独立性。分类和定位一般用的是2个独立的分支,这样使得2个任务之间缺乏交互,在预测的时候就会出现:得分高的预测位置不准,位置准的预测得分不高。
②任务无关的样本分配:对于分类最优的anchor和对于定位最优的anchor往往并不是同一个。
TAL(Task Aligned Learning)概述
TOOD提出任务对齐头(Task-aligned head, T-head)和新的任务对齐学习(Task-aligned Learning, TAL)来更明确地对齐两个任务;
TAL的操作流程:
- 首先,T-head对FPN特征进行预测。
- 然后,计算每个定位点的任务对齐度量,TAL根据此度量为T-head生成学习信号。
- 最后,T-head对分类和定位的分布进行相应的调整。其中,最对齐的锚通过概率图prob (probability map)获得更高的分类得分,通过学习偏移获得更准确的锚框预测。

TAL的具体实现
Task Alignment Learning: 为了进一步指导T-Head做出与任务对齐的预测提出
T
A
L
T A L
TAL 。
它包括一个分配策略和新损失的函数;
分配策略
(1)Task-aligned Sample Assignment:
对齐良好的针点应能联合精确定位预测出较高的分类分数;
不对齐的针应具有较低的分类评分,并随后予以抑制。
(2)Anchor alignment metric: 分类得分和loU的高阶组合来衡量任务对齐程度,
t
=
s
o
×
u
β
t=s^o\times u^\beta
t=so×uβ
其中:
s
s
s 和u分别表示分类分数和IOU值
(3)Training sample assignment:选择t值最大的
m
m
m 个针点为正样本,而使用其余的锚点作为负样本; 损失函数
L
c
l
s
−
p
o
s
=
∑
i
=
1
N
p
o
s
B
C
E
(
s
i
,
t
^
i
)
L_{c l s_{-} p o s}=\sum_{i=1}^{N_{p o s}} B C E\left(s_i, \hat{t}_i\right)
Lcls−pos=i=1∑NposBCE(si,t^i)
t
∧
t^{\wedge}
t∧ 是对
t
t
t 的归一化
ATSS
论文:《Bridging the Gap Between Anchor-based and Anchor-free Detection via Adaptive Training Sample Selection》
代码:sfzhang15/ATSS

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献31条内容
已为社区贡献31条内容





所有评论(0)