【深度学习】混合精度训练与显存分析
混合精度训练与显存分析关于参数精度的介绍可以见文章https://zhuanlan.zhihu.com/p/604338403相关博客。
关于参数精度的介绍可以见文章https://zhuanlan.zhihu.com/p/604338403
相关博客
【Megatron-DeepSpeed】张量并行工具代码mpu详解(三):张量并行层的实现及测试
【Megatron-DeepSpeed】张量并行工具代码mpu详解(一):并行环境初始化
【Megatron-DeepSpeed】张量并行工具代码mpu详解(二):Collective通信操作的封装mappings
【深度学习】【分布式训练】DeepSpeed:AllReduce与ZeRO-DP
【深度学习】混合精度训练与显存分析
【深度学习】【分布式训练】Collective通信操作及Pytorch示例
【自然语言处理】【大模型】大语言模型BLOOM推理工具测试
【自然语言处理】【大模型】GLM-130B:一个开源双语预训练语言模型
【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介绍
【自然语言处理】【大模型】BLOOM:一个176B参数且可开放获取的多语言模型
一、模型是如何训练的?
这里简单介绍前向传播、反向传播和优化过程,便于后续混合精度训练和显存分析的理解。
1. 前向传播
神经网络可以看作是大型拟合函数。不妨假设神经网络为 f ( x ; θ ) = g ( z ) , z = h ( x ) f(x;\theta)=g(z),z=h(x) f(x;θ)=g(z),z=h(x)。那么神经网络的前向传播过程:将样本 x x x送入函数 h h h,得到输出 z = h ( x ) z=h(x) z=h(x);然后将输出 z z z送入至函数 g g g得到最终的输出 g ( z ) g(z) g(z)。整个过程简化表示为 f ( x ; θ ) f(x;\theta) f(x;θ), θ \theta θ是模型的待学习参数。
2. 反向传播
反向传播这里仍然遵循前面的假设:神经网络 f ( x ; θ ) f(x;\theta) f(x;θ), x x x是输入, θ \theta θ是参数。此外,假设有 N N N个标注好的样本 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } \{(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)\} {(x1,y1),(x2,y2),…,(xN,yN)},其中 x i x_i xi是第 i i i个样本的取值, y i y_i yi则是对应的标签。现在,从从 N N N个样本中挑选 m m m个样本,组成一个batch { ( x 1 ′ , y 1 ′ ) , ( x 2 ′ , y 2 ′ ) , … , ( x m ′ , y m ′ ) } \{(x_1',y_1'),(x_2',y_2'),\dots,(x_m',y_m')\} {(x1′,y1′),(x2′,y2′),…,(xm′,ym′)}。那么模型在这 m m m个样本上的梯度为 g ^ = 1 m ∇ θ ∑ i = 1 m L ( f ( x i ′ ; θ ) , y i ′ ) \hat{g}=\frac{1}{m}\nabla_{\theta}\sum_{i=1}^m L(f(x_i';\theta),y_i') g^=m1∇θ∑i=1mL(f(xi′;θ),yi′)。
-
SGD
设 l r lr lr是模型的学习率,那么模型的优化过程则为:
θ ← θ − l r × g ^ \theta\leftarrow\theta-lr\times\hat{g} θ←θ−lr×g^ -
Adam
相比于SGD的优化过程,Adam通过引入两个变量来解决梯度震荡和动态学习率的问题。具体来说,初始化两个变量 v = 0 v=0 v=0和 r = 0 r=0 r=0,并指定两个超参数 β 1 \beta_1 β1和 β 2 \beta_2 β2。假设现在是 t + 1 t+1 t+1步的更新,并且batch的梯度 g ^ \hat{g} g^已经获得,那么有:
v = β 1 ⋅ v + ( 1 − β 1 ) ⋅ g ^ r = β 2 ⋅ r + ( 1 − β 2 ) ⋅ g ^ ⊙ g ^ v ^ = v 1 − β 1 t r ^ = r 1 − β 2 t Δ θ = v ^ r ^ + δ v=\beta_1\cdot v + (1-\beta_1)\cdot\hat{g}\\ r=\beta_2\cdot r+(1-\beta_2)\cdot \hat{g}\odot\hat{g} \\ \hat{v}=\frac{v}{1-\beta_1^t} \\ \hat{r}=\frac{r}{1-\beta_2^t} \\ \Delta\theta=\frac{\hat{v}}{\sqrt{\hat{r}}+\delta} v=β1⋅v+(1−β1)⋅g^r=β2⋅r+(1−β2)⋅g^⊙g^v^=1−β1tvr^=1−β2trΔθ=r^+δv^
其中, δ \delta δ是小常数,为了数值稳定通常设置为 1 0 − 8 10^{-8} 10−8。模型参数的更新过程为:
θ = θ − l r × Δ θ \theta = \theta - lr\times \Delta\theta θ=θ−lr×Δθ
二、混合精度训练
1. 精度
通常模型会使用float32精度进行训练,但是随着模型越来越大,训练的硬件成本和时间成本急剧增加。那么是否可以使用float16进行训练呢?答案是不适合。
float16的表示范围是 [ − 65504 ∼ 66504 ] [-65504\sim 66504] [−65504∼66504],表示精度是 2 − 24 2^{-24} 2−24。
- float16的优点
- 降低显存占用;float16比float32小一半,所有显存占用可以降低一半;
- 减少网络通信的开销;
- 硬件针对float16有优化,速度更快;
- float16的缺点
- 下溢。对于深度学习来说,float16最大的问题是"下溢"。模型的更新通常是 gradient × lr \text{gradient}\times\text{lr} gradient×lr,随着模型的训练,这个值往往会很小,可能会超出float16表示的精度。结果就是:大多数的模型权重都不再更新,模型难以收敛。
- 舍入误差。模型权重和梯度相差太大,通过梯度更新权重并进行舍入时,可能导致更新前和更新后的权重没有变化。
2. 原理
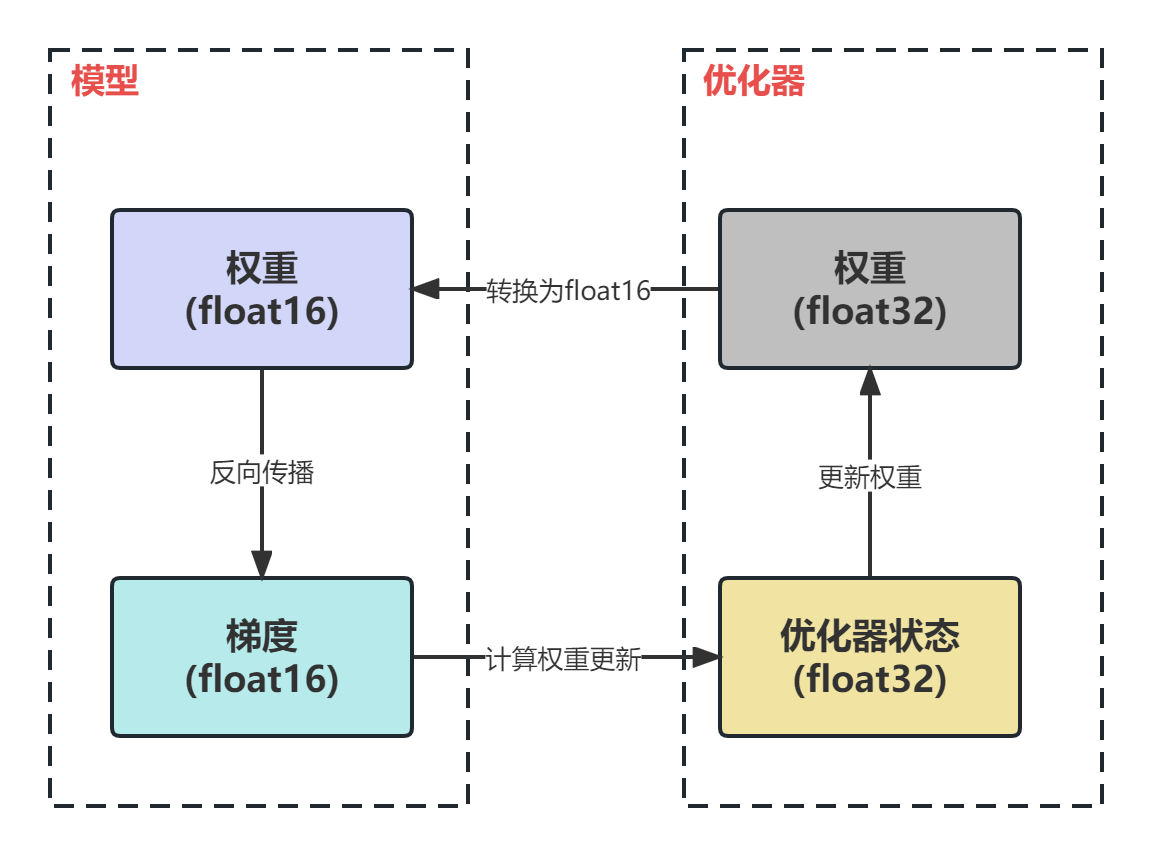
为了利用float16的优点并规避缺点,提出了混合精度训练。总的来说,混合精度训练中模型权重、梯度使用float16,优化器参数为float32。此外,优化器还需要保存一份float32版本的权重。

混合精度的具体过程如下:
- 使用float16权重进行前向传播;
- 反向传播得到float16的梯度;
- 通过优化器计算出float32精度的权重更新量;
- 更新float32权重;
- 将float32权重转换为float16;
3. 实战
-
apex。
apex是NVIDIA开发的混合精度训练工具,能够让用户快速实现混合精度训练。下面展示如何调用apex实现混合精度训练:
from apex import amp
###########
# 其他代码 #
###########
# 利用amp.initialize重新封装model和optimizer
model, optimizer = amp.initialize(model, optimizer, opt_level="O1")
# 其他训练代码
with amp.scale_loss(loss, optimizer) as scaled_loss:
scaled_loss.backward() #梯度自动缩放
optimizer.step() #优化器更新梯度
optimizer.zero_grad()
###########
# 其他代码 #
###########
amp.initialize(model, optimizer, opt_level="O1"),这里会指定混合精度的登记,共有4个级别:
O0:纯float32精度训练,可作为参照的baseline;
O1:根据黑白名单自动决定使用float16还是float32(推荐);
O2:绝大多数都使用float16,除了batch norm;
O3:纯float16,训练不稳定;
-
pytorch原生
pytorch在1.6版本后就支持混合精度训练了。下面是示例代码
from torch.cuda.amp import autocast as autocast, GradScaler ########### # 其他代码 # ########### scaler = GradScaler() ########### # 其他代码 # ########### # 前向传播过程中开启 with autocast(): output = model(input) loss = loss_fn(output, target) # float16精度范围有限,需要放大 scaler.scale(loss).backward() scaler.step(optimizer) scaler.update() ########### # 其他代码 # ###########
三、显存去哪了?
目前训练大模型基本上都会使用混合精度训练,基于前面关于混合精度训练的介绍来进一步分析显存的去向。
1. 主要的显存消耗
假设有一个参数量为 Ψ \Psi Ψ的模型,并使用Aadm作为优化器。首先,由于模型的参数和梯度使用float16,那么显存的消耗分别是 2 Ψ 2\Psi 2Ψ和 2 Ψ 2\Psi 2Ψ。Aadm会维护一个float32的模型副本,则会消耗 4 Ψ 4\Psi 4Ψ。此外,根据上面介绍的Aadm优化器,Adam需要为每个参数维护两个状态变量 v v v和 r r r。由于 v v v和 r r r均是float32,所以显存占用则为 4 Ψ + 4 Ψ 4\Psi+4\Psi 4Ψ+4Ψ。总的来说,模型会消耗 2 Ψ + 2 Ψ = 4 Ψ 2\Psi+2\Psi=4\Psi 2Ψ+2Ψ=4Ψ的显存,Aadm优化器则消耗 4 Ψ + 4 Ψ + 4 Ψ = 12 Ψ 4\Psi+4\Psi+4\Psi=12\Psi 4Ψ+4Ψ+4Ψ=12Ψ的显存。最终,总的显存消耗为 4 Ψ + 12 Ψ = 16 Ψ 4\Psi+12\Psi=16\Psi 4Ψ+12Ψ=16Ψ。对于GPT-2这样1.5B参数的模型,显存消耗至少 24 G B 24GB 24GB。
2. 剩余的显存消耗
激活(Activations)。 激活就是在前面"前向传播"过程中介绍的 z = h ( x ) z=h(x) z=h(x),在完成 g ( z ) g(z) g(z)之前显卡需要保存 z z z。显然,激活在训练中也会消耗大量的显存。一个具体的例子,模型为1.5B的GPT-2,序列长度为1K,batch size为32,则消耗显存为60GB。Activation checkpointing(或者activation recomputation)则是一种常见的降低激活占用显存的方法。该方法以33%的重计算为代价,将激活的显存占用减少至总激活的均分更。即激活显存占用从60GB降低至8GB。
尽管激活的显存占用已经显著减少,但是对于更大的模型来说,激活所占用的显存也会非常大。例如,对于100B参数量的GPT模型且batch size为32,即使用来activation checkpointing,显存占用也需要60GB。
临时缓存区(Temporary buffers)。对于大模型,用于存储中间结果的临时buffer也会消耗大量显存。例如在all-reduce时,需要一个平坦的buffer来融合所有的梯度,从而改善吞吐量。例如,跨设备的all-reduce操作会随着消息的增大而增加。虽然,梯度本文是fp16的张量,但是有些操作中可能需要融合的buffer为fp32。当模型尺寸很大时,临时的buffer也不小。例如,对于1.5B参数的模型,一个fp32的buffer需要6GB的显存。
显存碎片。即使在有足够显存的情况下,也可能会导致Out of Memory,这是由于显存碎片导致的。在进程发出显存请求时,如果没有连续的显存来满足请求,即使总的显存仍然足够,该请求也会失败。当训练非常大的模型时,可以观察到明显的显存碎片。极端情况下,可能会导致30%的显存碎片。
参考资料
https://arxiv.org/pdf/1910.02054.pdf
https://zhuanlan.zhihu.com/p/103685761
https://zhuanlan.zhihu.com/p/604338403
https://blog.csdn.net/flyingluohaipeng/article/details/128095936
https://zhuanlan.zhihu.com/p/406319979

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献13条内容
已为社区贡献13条内容





所有评论(0)