【深圳大学大物实验】RLC电路谐振特性的研究

本次实验完成较为圆满，误差来源主要是仪器精度和作图后取点精度。思考题：1.已知R ,L,C分别为电路的总电阻，总电感，总电容，f0 ,f1 , f2分别谐振频率和通频带对应的频率，求证：2、实验中，当RLC串联电路发生谐振时，是否有 UL =UC和UR =U（UR为电阻上的电压，U为电源电压，UL为电感上电压，UC为电容电压）？若关系不成立，分析原因。答：1、Q=w0L/R=1/w0CR=√(L/

归忆886

2741人浏览 · 2024-01-26 22:03:08

归忆886 · 2024-01-26 22:03:08 发布

预习题目

一、单选题共 19 小题共 95 分得 95 分
1. (5分)RLC串联电路发生谐振时，电压和电流之间的相位差为（）
标准答案： C
学生答案： C √
学生得分： 5
A. π/2
B. π
C. 0
D. 3π/2
2. (5分) RLC串联电路中，保持电源电压不变，谐振时下列说法正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. 电路中电抗和电流都最小
B. 电路中电抗最大，电流最小
C. 电路中电抗最小，电流最大
D. 电路中电抗和电流都最大
3. (5分) 关于RLC串联电路谐振时的电抗特性，正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. 纯电感性
B. 纯电容性
C. 纯电阻性
D. 阻抗，容抗，感抗都有
4. (5分) 关于品质因数Q与谐振峰的关系，正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. Q值越小，谐振峰越高
B. Q值大小与谐振峰高低无关
C. Q值越大，谐振峰越高
5. (5分) 关于RLC串联电路Q值与谐振曲线带宽的关系，正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. Q值越大，带宽越宽
B. Q值与带宽无关
C. Q值越大，带宽越窄
6. (5分) RLC串联电路中，其它条件不变时，品质因数Q值与R的关系，正确的是（）
标准答案： A
学生答案： A √
学生得分： 5
A. R越小， Q值越大
B. Q的大小与R无关
C. R越大， Q值越大
7. (5分) RLC串联电路中，其它条件不变时，品质因数Q值与C的关系，正确的是（）
标准答案： A
学生答案： A √
学生得分： 5
A. C越小， Q值越大
B. Q的大小与C无关
C. C越大， Q值越大
8. (5分) RLC串联电路中，其它条件不变时，品质因数Q值与L的关系，正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. L越小， Q值越大
B. Q的大小与L无关
C. L越大， Q值越大
9. (5分) RLC串联电路中品质因数Q值与能量存储效率的关系，正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. Q值越小，能量储存效率越高
B. 能量储存效率与品质因数无关
C. Q值越大，能量储存效率越高
10. (5分)
RLC串联电路谐振时，电源电压U0=2V,电容上电压UC=25V，电阻上电压UR=1.6V， Q值计算结果
为（）
标准答案： C
学生答案： C √
学生得分： 5
A. 1.25
B. 15.625
C. 12.5
D. 0.8
11. (5分) RLC串联电路中，谐振频率 =3000Hz,通频带对应频率 =2800Hz ,
=3200Hz,Q值计算结果为（）
标准答案： C
学生答案： C √
学生得分： 5
A. 7
B. 8
C. 7.5
D. 14
12. (5分) RLC串联电路谐振时，电容和电感上电压的相位差是（）
标准答案： B
学生答案： B √
学生得分： 5
A. π/2
B. π
C. 0
D. 3π/2
13. (5分) 关于串联和并联谐振说法正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. 串联谐振和并联谐振都是电压谐振
B. 串联谐振叫电流谐振，并联谐振叫电压谐振
C. 串联谐振叫电压谐振，并联谐振叫电流谐振
D. 串联谐振和并联谐振都是电流谐振
14. (5分) RLC并联电路谐振时，电容和电感上电流的相位差是（）
标准答案： B
学生答案： B √
学生得分： 5
A. π/2
B. π
C. 0
D. 3π/2
15. (5分) RLC并联电路谐振时，关于电容和电感上电流说法正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. 大小不等，相位相同
B. 大小相等，相位相同
C. 大小相等，相位相反
D. 大小不等，相位相反
16. (5分)RLC并联电路谐振时，电流一定的情况下，说法正确的是
标准答案： C
学生答案： C √
学生得分： 5
A. 阻抗最小，电压有效值最大
B. 阻抗最大，电压有效值最小
C. 阻抗最大，电压有效值最大
D. 阻抗最小，电压有效值最小
17. (5分) RLC串联电路谐振频率，说法正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. 与RLC都有关
B. 与RC有关
C. 与LC有关
D. 与RL有关
18. (5分) RLC并联电路谐振频率，说法正确的是（）
标准答案： A
学生答案： A √
学生得分： 5
A. 与RLC都有关
B. 与RC有关
C. 与LC有关
D. 与RL有关
19. (5分) RLC并联电路Q值与通频带带宽Δf 的关系，正确的是（）
标准答案： C
学生答案： C √
学生得分： 5
A. Q越小，带宽越小
B. Q的大小与带宽的大小不相关
C. Q越大，带宽越小
二、多选题共 1 小题共 5 分得 5 分
1. (5分)本实验的实验目的是（）
标准答案： ABC
学生答案： ABC √
学生得分： 5
A. 学习绘测RLC电路谐振曲线的方法
B. 绘测RLC串联电路在 R 分别为 100 和 200 欧姆时的谐振 I-f 曲线
C. 研究交流电路的谐振现象

一、实验目的

1.研究交流电路的谐振现象，认识RLC电路的谐振特性；

2.学习测绘RLC电路谐振曲线的方法 .

3.测绘串联电路在R =100Ω 、R =200Ω谐振f – I曲线

二、实验原理

1.RLC串联谐振：

（1）串联谐振现象及谐振频率：

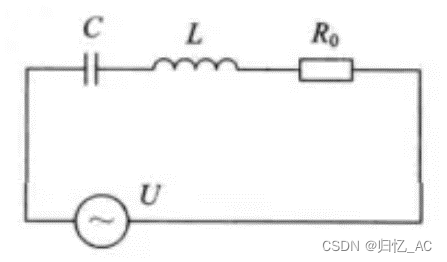
图1

RLC串联谐振电路如图1所示，其交流电压和交流电路I的关系为

其中，称为交流电压的阻抗，L是电感的自感系数，C是电容器的容值，

R是电路中的电阻，w是交流电源的圆频率，U是交流电源的输出电压的有效值。

电压与电流的相位差为

当时，电压和电流间的相位差为0，此时电路中阻抗Z达到极小，电流I达到最大值Imax，整个电路呈纯电阻性，这种现象叫做谐振现象此时的圆频率称为谐振圆频率ω0，

ω0大小为

，谐振频率

保持电压不变，RLC 串联电路电流和电源的频率的关系曲线如图2所示

图2

（2）品质因数Q及带宽：

RLC串联电路谐振时，电感上的电压UL=ω0LI和电容上的电压UC=IC/ω0大小相等，相位相反，总电压为U=RI，通常情况下，谐振电路的R比起容抗、感抗来说小得多，所以UL和UC比总电压大许多倍，这个倍数称为谐振电路的品质因数Q，即

因为Q一般都大于1，所以串联谐振也叫电压谐振。

Q除了反映电路的电压分配之外，也反映电路存储能量的效率。RLC串联电路谐振时，能量在电容和电感之间来回震荡，在震荡过程中能量有一部分变成焦耳热消耗在电阻上，为了维持震荡，外电路就要不断输入能量，由上式也可以看出，电阻越小，Q值越大，存储能力的效率就越高。

Q值也决定了电路的频率选择性能。为了定量描述频率选择性能，把在谐振峰两边的电流有效值处（电流最大值除以根号2）处对应频率之间的宽度△f=f2-f1称为通频带宽，简称带宽，如图2所示。Q值越大，峰越高，带宽越窄，电路的频率选择性越强。

Q值和带宽的关系为

三、实验仪器

DH4503型实验仪、固玮数字示波器

四、实验内容

１、测定串联电路的谐振曲线

（1）分别取R=100Ω和R=200Ω进行测量两条谐振曲线

（2）测量谐振频率

（3）做出串联电路的谐振曲线

（4）测定共振频率和共振时的UR、UC和UL

（5）谐振频率的理论值和测量值比较

（6）计算Q值,进行比较

注意:

(1)共地问题。被测电压的元件必须和电源共地。

(2)测量共振频率及共振时的作图时,将这一组数据（f0、UR)插入.

采用下面的四种方法计算品质因数Q：

1.Q=w0L/R，理论计算

2.Q=Ul/U

3.Q=Uc/U

4.Q=f0/(f1-f2)

五、数据记录

L=100mH、C=4.4×10-8F、U=1V

f /Hz	R= 100Ω		R=200Ω		f /Hz	R=100Ω		R= 200Ω
f /Hz	u/mV	i/mA	u/mV	i/mA	f /Hz	u/mV	i/mA	u/mV	i/mA
1600	85.8	0.858	169	0.845	2400	680	6.8	825	4.125
1700	103	1.03	283	1.415	2450	641	6.41	811	4.055
1800	124	1.24	239	1.195	2500	510	5.1	732	3.66
1900	152	1.52	290	1.45	2550	444	4.44	683	3.415
2000	195	1.95	365	1.825	2600	369	3.69	607	3.035
2200	400	4	628	3.14	2900	172	1.72	331	1.655

R0=100Ω时：共振频率的理论值f0=2400Hz，共振频率的测量值为2376Hz，达到共振时UR=978mV，UL=8.44V，UC=8.44V。

R0=200Ω时：共振频率的理论值f0=2400Hz，共振频率的测量值为2385Hz，达到共振时UR=839mV，UL=4.86V，UC=4.86V。

六、数据处理

1.串联电路的谐振曲线

2. 2.谐振频率的理论值和测量值比较：

R0=100Ω时：共振频率的理论值为f0=2400Hz，共振频率的测量值为2376Hz，相对误差=（2376Hz-2400Hz）/2400Hz×100%= -1.00%

R0=200Ω时：共振频率的理论值为f0=2400Hz，共振频率的测量值为2397Hz，相对误差=（2385-2400Hz）/2400Hz×100%= -0.625

两个测量值均低于理论值。

3.计算Q值，进行比较：

R=100Ω时：Q=w0L/R=14.92，Q=Ul/U=8.44，Q=Uc/U=8.44，Q=f0/(f1-f2)=8.25.

R=200Ω时：Q=w0L/R=7.53，Q=Ul/U=4.86，Q=Uc/U=4.86，Q=f0/(f1-f2)= 4.55。

使用四种方法计算Q值，发现使用Q= f0/(f1-f2)计算得到的结果最小，原因可能是作图软件不能准确按照图线求出未知点坐标，存在-定误差，以及在寻找电流最大值时可能并未找到真正的最大值导致Q值偏低;使用Q= w0L/R公式计算得到的结果最大，原因可能是使用该公式计算时R未将电感电阻计入导致Q值偏大。