目录

一、理论基础

二、核心程序

三、仿真结论

---

一、理论基础

       双边带调幅（DSB-SC，Double Sideband Suppressed Carrier）是一种模拟调制技术，用于在传输信号时抑制了载波信号。它是一种调幅（AM，Amplitude Modulation）的变种，旨在降低信号的频带占用，减少无用的频谱能量。

       在 DSB-SC 调制中，原始信号被用来调制两个边带，而不是传统的调幅方法中会同时调制一个边带和一个载波信号。这使得 DSB-SC 调制的频带占用比较紧凑，从而节省了频谱资源。然而，DSB-SC 也存在一些问题，例如它需要较复杂的解调过程，并且在信号传输过程中容易受到相位偏移等干扰。

DSB-SC 调制的主要特点包括：

• 双边带调幅的信号只包含了两个边带，没有了载波信号，因此相对于全调幅（AM）来说，节省了频谱。
• DSB-SC 调制需要较复杂的解调过程，通常需要同步解调器的相位。
• DSB-SC 调制可以通过载波同步来实现，从而在解调器端恢复出原始信号。

       尽管 DSB-SC 调制在频带占用方面有一定的优势，但由于其解调过程的复杂性，以及容易受到相位偏移的干扰，它在数字通信系统中并不常见。更先进的调制技术如单边带调幅调制（SSB-AM）和调频调幅（FM）通常在实际应用中更受青睐。

      双边带调幅（DSB-SC）是一种模拟调制技术，它在传输信号的同时传输信号的两个边带，从而降低了频带占用。下面我会详细介绍 DSB-SC 调制和解调系统的原理、公式以及实现过程。

单边带:只传送一个边带的调制方式成为单边带调制。

       AM、DSB的共同缺点：所需传输的带宽是信号的2倍，这样就降低了系统的有效性。由于从信息传输的角度讲，上、下两个边带所包含的信息相同，因此只传送一个边带即可以传送信号的全部信息。

       双边带调制：由于AM信号在传输信息的同时，也同时传递载波，致使传输效率太低，造成功率浪费。既然AM系统的载波并不携带信息，所以不发送载波仍能传输信号。

        DSB-SC 调制通过将原始信号与载波信号相乘，从而得到双边带调幅信号。其调制原理可以用以下公式表示：

       DSB-SC 解调可以使用同样的载波信号进行相乘，从而得到原始信号的调制。解调原理可以用以下公式表示：

DSB信号主要有以下的特点：
1、幅度调制。DSB信号是过调幅AM波，故它仍是幅度调制，但此时包络已不再与m(t) 成线性关系变化，这说明它的包络不完全载有调制信号的信息，因此它不是完全的调幅波。
2、幅度调制，频率未变。DSB信号的频率仍与载波相同，没有受到调制。
3、有反相点。DSB信号在调制信号的过零点处出现了反相点，调制指数大于1的AM信号在调制信号过零点处出现反相点。所以有反相点出现，是因为调制信号在过零点前后取值符号是相反的。

       调制和解调单边带调制和解调的方法有多种，其中最常用的是滤波法。用滤波法实现单边带调制，是分双边带信号形成和无用边带抑制两步完成的。双边带信号由平衡调制器形成。由于调制器的平衡作用，载频电平被抑制到很低。对无用边带的抑制，是由紧跟在平衡调制器后面的边带滤波器完成的。边带滤波器是一带通滤波器，若下边带为无用边带，则恰当地选择其中心频率和通带宽度，让上边带信号通过而抑制下边带。当需要形成多路独立边带信号时，就需要有相应数目的单边带信号产生器，它们具有不同的载频和不同中心频率的边带滤波器。然后把这些占有不同频段的单边带信号线性相加，便可得到多路独立边带信号。
　　单边带信号的解调，除了载频全发送的兼容单边带和残留单边带可以用包络检波外，其他各类单边带的解调只能用单边带产生的相反过程来完成（图3b），即仍用平衡调制器完成单边带信号频谱向基带的平移，并通过紧跟在调制器后面的低通滤波器，提取有用的基带信号，抑制无用的边带信号。
　　用滤波法产生和解调单边带信号，通常都在低于工作频率的低载频上进行。因此，在单边带产生器后和单边带解调器前有一个频率搬移部分，把单边带信号频谱从低载频搬移到工作频率，或相反。除滤波法外，还有相位补偿法和合成法可以在工作频率上直接产生单边带信号，但由于性能都不如滤波法，所以很少采用。

二、核心程序

.......................................................
ylabel('幅度')
grid
xlim([-0.1,0.1])
%（4）利用matlab绘制已调信号
y4=sinc(t*200).*cos(2*pi*200*t) %%已调信号
subplot(2,3,4),plot(t,y4,'r-')
title('已调信号')
xlabel('时间：s')
ylabel('幅度')
grid
xlim([-0.05,0.05])
%(5) 利用matlab绘制已调信号的频谱
fs1=1000  %已调信号频谱
yk=fft(y4,5000)         %对信号做傅立叶变换
yw=2*pi/4000*abs(fftshift(yk))    %频谱搬移
fw=[-2500:2499]/5000*fs1
subplot(2,3,5),plot(fw,yw,'r-')
title('已调信号的频谱')
xlabel('频率：hz')
ylabel('幅度')
grid
xlim([-400,400])
%（6）利用matlab绘制DSB-SC调制信号的功率谱密度
[c,lags]=xcorr(y4,200) %%DSB信号自相关函数
figure             %200表示自相关函数时间т
subplot(211)   
plot(lags/fs,c)
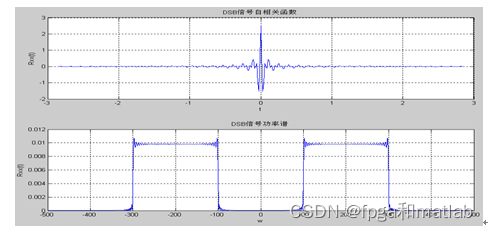
title('DSB信号自相关函数')
xlabel('t')
ylabel('Rxx(t)')
grid

SDSBp=fft(c,5000) %%DSB功率谱
fw=[-2500:2499]/5000*fs1
yw=2*pi/4000*abs(fftshift(SDSBp))%频谱搬移
subplot(212)
plot(fw,yw)
title('DSB信号功率谱')
xlabel('w')
ylabel('Rxx(t)')
grid
%（7）利用matlab绘制相干解调后的信号波形

y7=y4.*y3  %%解调信号
figure
subplot(211)
plot(t,y7)
title('解调信号')
xlabel('时间：s')
ylabel('幅度')
grid
xlim([-0.1,0.1])
.............................................................
up120

三、仿真结论

            通信中，调制信号通常是平稳随机过程。其功率谱密度与自相关函数之间是一对付氏变换关系。此时先求调制信号的自相关函数，利用命令[c,lags]=xcorr(y4,20)以及plot(lags/fs,c)就可以实现调制信号的自相关函数，此时将自相关函数求付氏变换。利用SDSBp=fft(c,5000； fw=[-2500:2499]/5000*fs；yw=2*/4000*abs(fftshift(SDSBp))即可实现，此时用figure和subplot可以在另一页画出自相关函数波形和功率谱密度波形，具体图形如图1：